汎用GNN力場M3GNetによる教師データの生成とNeural Network力場の学習#

ナノ材料統合GUI Advance/NanoLaboには、LAMMPSによる分子動力学計算のトラジェクトリから、ニューラルネットワーク分子動力学システムAdvance/NeuralMDで使用可能な教師データを生成する機能が実装されています。この機能を用いると、DFTを用いた教師データ生成に比べて、大幅に短い時間で教師データを生成することができます。

本解析事例では、Si及びSiCについて、汎用グラフニューラルネットワーク(GNN)力場M3GNetを用いた分子動力学計算によって教師データを生成し、それらを用いてNeural Network (NN)力場の学習を行います。このようにして学習したNN力場は、教師データ生成に用いた任意の系について、M3GNetと同程度の精度を保ちつつ、M3GNetよりも高速に計算を実行することが可能です。また、本解析事例では、力場の性能を評価・比較するために、各力場を用いてSi及びSiCのヤング率の計算も行います。

M3GNetによる教師データの生成#

Materials Project¹より取得したダイヤモンドSiのユニットセルモデル(mp-149)及び3C-SiCのユニットセルモデル(mp-8062)のそれぞれについて、M3GNetを用いた分子動力学計算を実行し、教師データを生成しました。

NPTアンサンブルのもとで、温度は300K、圧力は1barで一定とし、セル変形の制約としてはTriclinicを選択しました。時間の刻み幅は0.5 fsとし、ステップ数は500000ステップ(250 ps)としました。

教師データの生成に関する設定は、User's画面のUser's Additional Settings into Input-fileの欄にdump nnpdump all nnp 100 sannp.trainと入力するだけで完了します。このように入力した場合は、100ステップごとに全原子の情報がsannp.trainという教師データファイルに書き込まれますが、ステップ数、対象原子、ファイル名は必要に応じて変更することが可能です。

以上の条件のもとで計算を実行し、Si及びSiCそれぞれについて5001個ずつの教師データを生成しました。

Si及びSiCの分子動力学計算はそれぞれ1時間10分、1時間28分で完了しており²、DFT計算を用いる場合に比べて大幅に短い時間で教師データを生成できていることがわかります。


Siモデル	SiCモデル

Neural Networkの学習#

Si及びSiCそれぞれについて、前節で生成した教師データを用いてNN力場の学習を行いました。

学習の条件は以下のように設定しました。

Δ-NNP法：ON (LJ-like Potential)
対称関数 : Chebyshev多項式(動径成分50個、角度成分30個)
カットオフ関数 : tanh(1-r/r0)^3 (カットオフ半径 6 Å)
Neural Network構造 : 2層×40ノード×16モデル³
活性化関数:twisted tanh
Super Epoch³あたりのEpoch数:500
Super Epochあたりの教師データ数:500
エネルギーの収束閾値 : 0.001 eV/atom
力の収束閾値 : 0.01 eV/Å

なお、教師データのうち10%はテストデータとして分離し、残りの90%を学習に使用しました。

学習及びテストの結果得られたNN力場のRMSEを次の表に示します。

	エネルギーの RMSE(学習) (eV/atom)	エネルギーの RMSE(テスト) (eV/atom)	力の RMSE(学習) (eV/Å)	力の RMSE(テスト) (eV/Å)
Si	4.905×10^-3	5.175×10^-3	4.792×10^-2	5.040×10^-2
SiC	3.058×10^-2	2.681×10^-2	1.320×10^-1	1.646×10^-1

また、SiのNN力場の学習⁴及びSiCのNN力場の学習⁵はいずれも10分程度で完了しました。

ヤング率の計算#

M3GNet及び前節で生成したNN力場を用いて、Si,SiCそれぞれの2×2×2スーパーセルモデルについて分子動力学計算を行い、その結果からヤング率を算出しました。

本事例では、以前のNi単結晶のヤング率の異方性の計算と同様にして、一定の速度でセルを変形させた際の応力の変化を計算しました。ただし、平衡化スキームのステップ数を5000ステップ(5 ps)、一軸応力スキームを500000ステップ(500 ps)とし、セル変形のレートは<100>方向に2×10^-4 Å/psとしました。

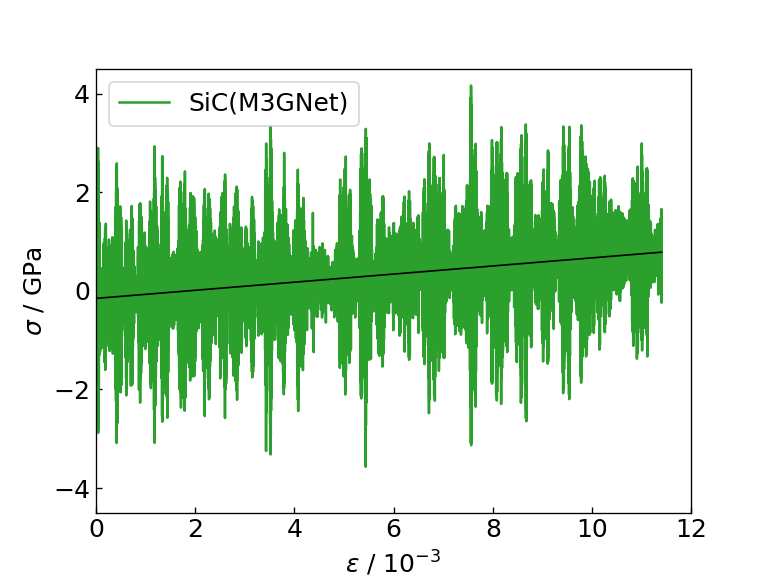
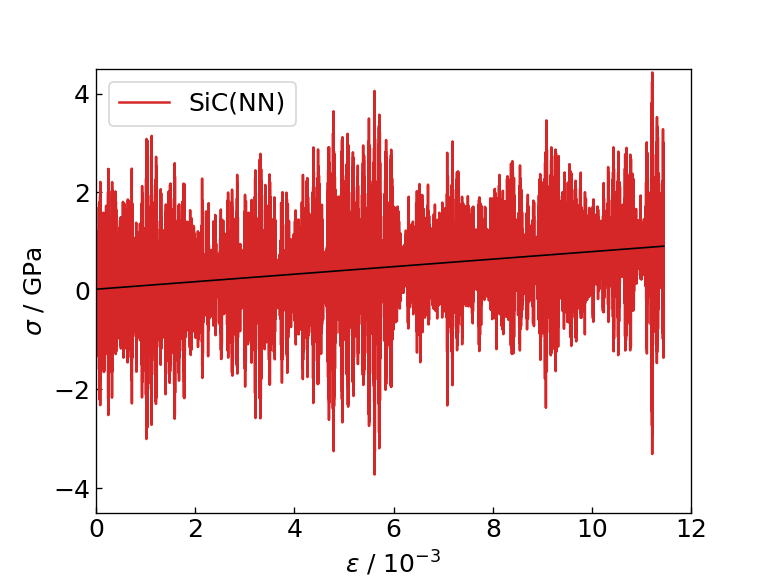
計算の結果得られた、ひずみ $\epsilon$ に対する応力 $\sigma$ の応答のグラフと、その一次関数フィッティング(黒の実線)の傾きとして求めたヤング率、それぞれの計算に要した時間を以下の図及び表に示します。また、比較のために、DFT計算によって求められたSi及びSiCのヤング率の文献値もあわせて表に示します。


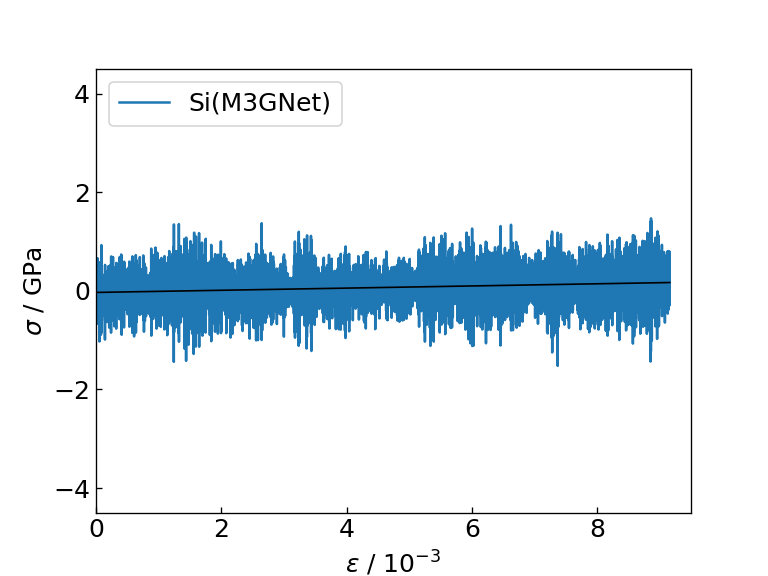
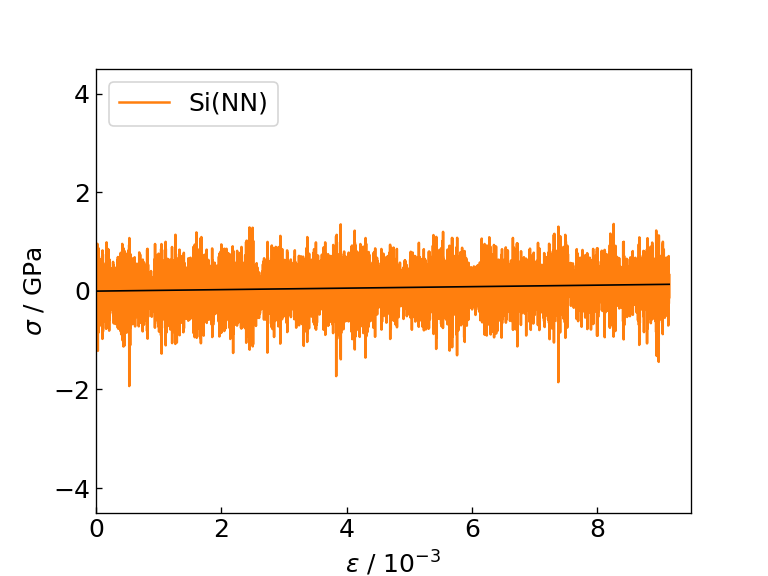
Si(M3GNet)のひずみ-応力図	Si(NN)のひずみ-応力図

SiC(M3GNet)のひずみ-応力図	SiC(NN)のひずみ-応力図

	M3GNetによるヤング率 (GPa)	NN力場によるヤング率 (GPa)	DFTによるヤング率 (GPa)
Si	22	15	138.5⁶
SiC	82	76	362⁷

	M3GNetによる計算時間	NN力場による計算時間
Si	3時間57分²	25分⁴
SiC	7時間51分²	55分⁵

図及び表からは、NN力場はM3GNetと同程度の精度で、ひずみに対する応力の応答及びヤング率を計算できていることがわかります。それにもかかわらず、NN力場を用いた場合はM3GNetに比べて約8倍の速度で計算を実行できており、NN力場はM3GNetに比べてより大きな系の計算にも適用可能であることがわかります。

なお、M3GNet及びNN力場により計算したヤング率は、DFT計算によって求められたヤング率に比べて小さく見積もられていますが、これは配布されているM3GNetの学習済みモデル(MP-2021.2.8-EFS)のSi及びSiCのヤング率に対する計算精度に起因すると考えられます。一方で、M3GNet及びNN力場のいずれの場合においても、SiとSiCのヤング率の大小関係については定性的に正しく計算できていることが表からわかります。

以上の結果から、Advance/NanoLabo及びAdvance/NeuralMDを用いることで、ある特定の系に対して汎用力場と同程度の精度を保ちつつ、大幅に短い時間で計算を実行可能なNN力場を生成できることがわかりました。この機能を用いることで、これまで汎用力場では計算できなかった大規模な系での計算も比較的短時間で実行できることが期待されます。

汎用GNN力場M3GNetによる教師データの生成とNeural Network力場の学習#

M3GNetによる教師データの生成#

Neural Networkの学習#

ヤング率の計算#

関連ページ#