複数Neural Networkモデルを用いた核燃料材料の融点解析#
複数Neural Networkモデルの平均値を用いた力場表現#
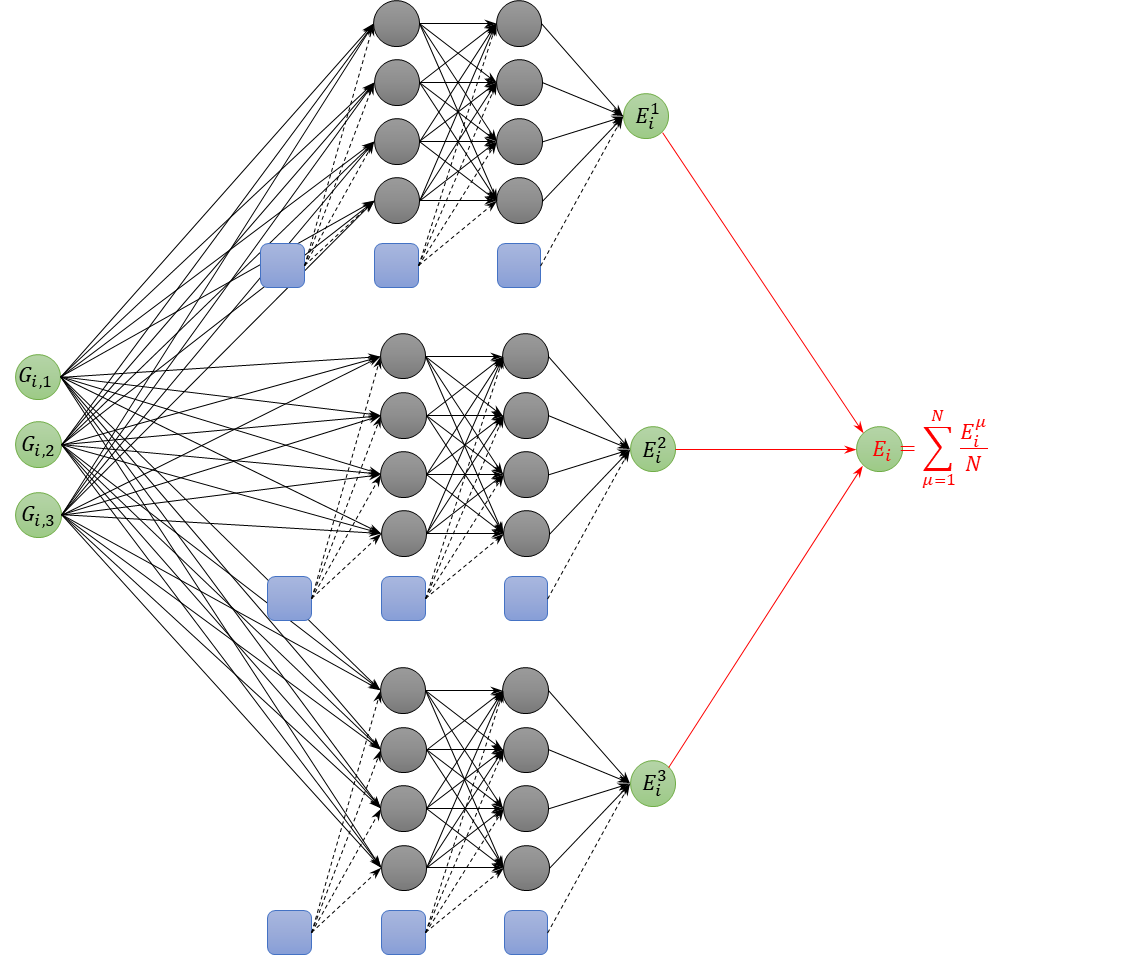
NeuralMDでは、各原子の化学環境を表現した対称関数を入力データとした多層パーセプトロンをNeural Network力場としています。この多層パーセプトロンはエネルギーを出力するわけですが、Ver.1.9では複数の多層パーセプトロンを用意してその平均値でエネルギーを表現するという新しい機能が実装されました。当該手法は ANI-2xなどでも採用されており、分子動力学計算の過程で出現する構造が教師データに含まれないような外挿領域にあっても、単一の多層パーセプトロンを用いる場合に比べて精度よく計算できることが知られています。Neural Network力場の安定性が向上するため、特に、無機材料が溶融した状態やアモルファス材料に対して有効です。Δ-NNP法および自己学習ハイブリッドモンテカルロ法と併用することで、比較的に少ない数の教師データであっても、安定した力場が容易に作成できるようになりました。当該手法でのNeural Network力場を図示すると、図1のようになります。
また、当該手法を適用すると最適化すべき変数(多層パーセプトロンの重みとバイアス)が増えるため、Neural Network力場の学習処理に多くの計算時間が掛かります。そこで、学習処理の高速化を目的としてSuper Epoch法を実装します。Super Epoch法では教師データを複数のサブセットに分割して、各サブセットを使ったL-BFGS法による学習処理を連続して実行します。例えば、教師データが10,000個ある場合、500個の教師データを含む20個のサブセットに分割します。先ずは最初の500個の教師データを用いてL-BFGS法で数百エポック程の学習を実施します。その後、別の500個の教師データに切り替えて学習を行います。これを20回繰り返します。これにより1エポック当たりの計算量を低減させつつ、一つのサブセット内では対称関数およびその微分をメモリー上で共有することでエポック毎の対称関数計算を回避できます。さらに、500構造分の対称関数の情報のみをメモリーに格納すればよいので、メモリー使用量の大幅な低減も実現しました。
分子動力学計算においては、計算のボトルネックは対称関数およびその微分にあるため、Neural Networkモデルが複数に増えても計算時間への影響は無視できる程度に小さいです。
 |
|---|
| 図1 |
CeO2/UO2/PuO2の溶融#
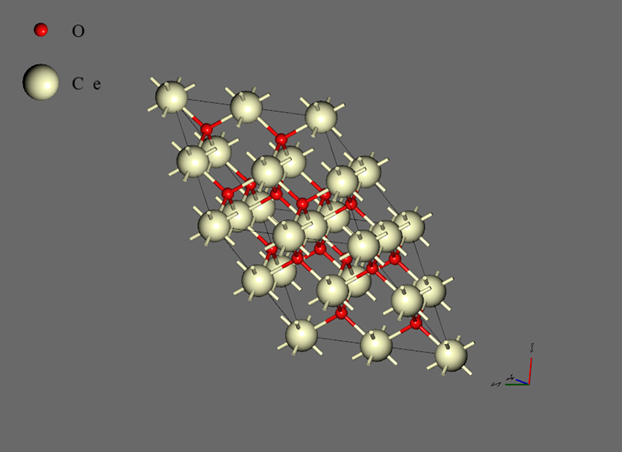
複数Neural Networkモデルを用いた手法は無機材料の溶融などに適しているため、本件ではCeO2、UO2、PuO2の溶融状態に対応したNeural Network力場を作成して融点の評価を行います。Neural Network力場の作成に当たっては、NPTアンサンブルでの自己学習ハイブリッドモンテカルロ法を適用します。NPTアンサンブルにおける温度は4000K、圧力は1.0bar、セル形状の自由度はTriclinicとしました。結晶構造は蛍石型のプリミティブセルをベースとして、2 x 2 x 2 のスーパーセルを用いました(図2)。原子数は24個です。第一原理計算およびNeural Network力場の計算条件は下記の表1、表2の通りです。
 |
|---|
| 図2 |
| 第一原理計算の条件 | 設定値 |
|---|---|
| 擬ポテンシャル | 【CeO2】Ce.GGA-PBE-paw-v1.0.UPF, o_pbe_v1.2.uspp.F.UPF 【UO2】U.pbe-spfn-rrkjus_psl.1.0.0.UPF, O.pbe-n-rrkjus_psl.1.0.0.UPF 【PuO2】Pu.pbe-spfn-rrkjus_psl.1.0.0.UPF, O.pbe-n-rrkjus_psl.1.0.0.UPF |
| カットオフエネルギー | 【CeO2】40Ry, 360Ry 【UO2】47Ry, 420Ry 【PuO2】93Ry, 839Ry |
| k点サンプリング | 2 x 2 x 2 |
| スピン分極 | 無し |
| 交換相関汎関数 | GGA-PBE |
| NN力場の条件 | 設定値 |
|---|---|
| Δ-NNP法 | Lennerd-Jones-likeポテンシャルを適用 |
| 対称関数 | Chebyshev多項式(動径成分:40個, 6.0Å、角度成分:30個, 6.0Å) |
| NNモデル | 32モデル x 2層 x 35ノード |
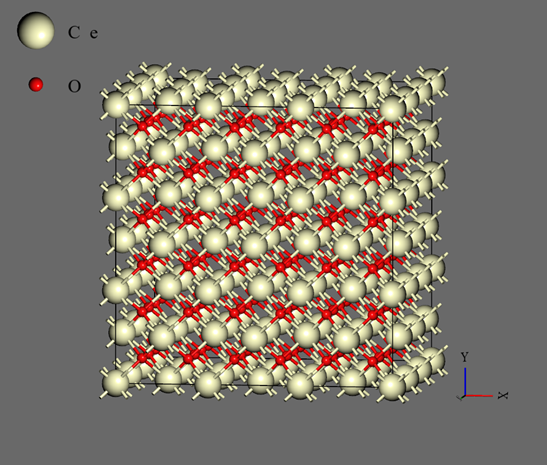
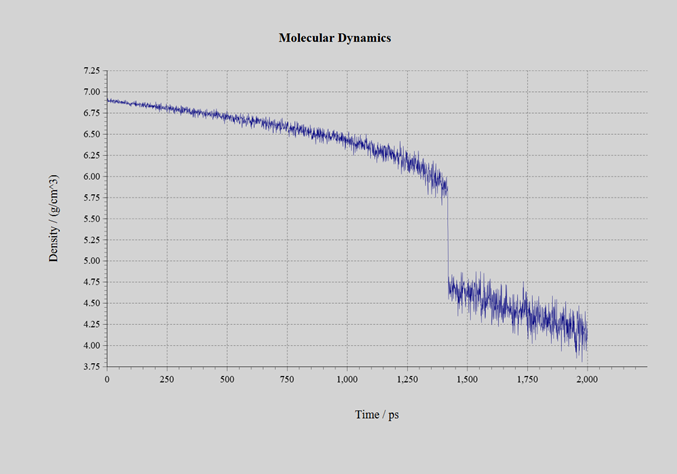
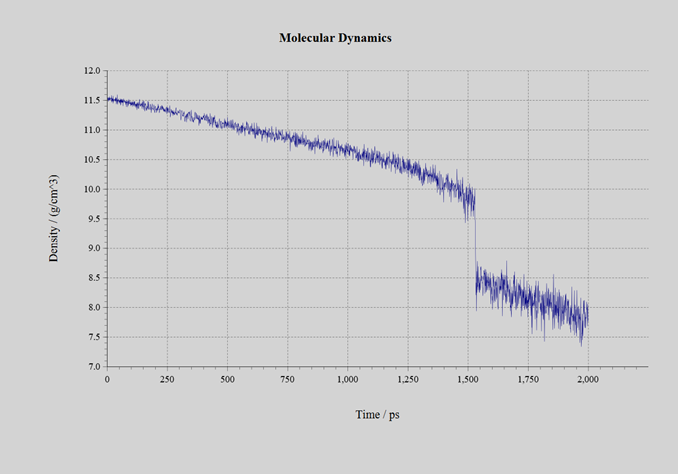
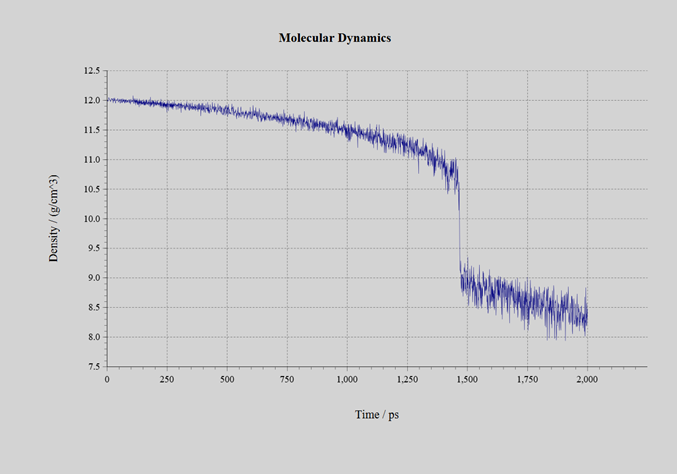
自己学習ハイブリッドモンテカルロ法の過程で生成された教師データの数は、CeO2では1634個、UO2では650個、PuO2では1078個です。いずれも初期構造では蛍石型の結晶としていたものの、計算の過程で溶融しており、最終的に蒸発またはセル形状が過剰に扁平するまで計算を継続しました。自己学習ハイブリッドモンテカルロ法にて得られたNeural Network力場を用いて、分子動力学計算を実施しました。作成された力場のRMSEは表3の通りです。計算に用いたモデルは 3 x 3 x 3 のスーパーセル(324原子系:図3)です。NPTアンサンブルにて、時間刻み幅を1.0fsとして2.0nsのシミュレーションを実施しました。圧力は1.0barとしてセル形状はIsotropicに拘束しました。初期温度は300Kで、2.0ns後の温度が3500Kとなるように線形に昇温しました。シミュレーションの過程で、材料は溶融して固体から液体へと変化します。密度の変化を下記の図4、5、6に示します。1.4~1.6ns近傍で密度が不連続に変化している箇所が見受けられます。この時点での温度が融点です。各材料の融点は、下記の表3の通りです。600~1600個という非常に少ない教師データ数でありながら、融点の実験値を定性的には正しく再現できています。
 |
|---|
| 図3 |
|
|
|
図4:CeO2 |
図5:UO2 |
図6:PuO2 |
| エネルギーのRMSE | 力のRMSE | 融点の計算値 | 融点の実験値 | |
|---|---|---|---|---|
| CeO2 | 0.020 eV/atom | 0.29 eV/A | 2299℃ | 約2400℃ |
| UO2 | 0.018 eV/atom | 0.29 eV/Å | 2476℃ | 約2800℃ |
| PuO2 | 0.018 eV/atom | 0.29 eV/Å | 2376℃ | 約2400℃ |