TEM回折パターンの第一原理シミュレーション: Cu-Au規則合金と超格子反射#

PHASE logo

透過型電子顕微鏡（TEM）は、ナノスケールの物質の結晶構造を評価するための強力なツールです。特に、TEMで得られる電子回折パターンは、原子の配列に関する豊富な情報を含んでいます。本解析では、第一原理計算ソフトウェアAdvance/PHASEと連携するPythonライブラリであるPymatgenを用い、Cu-Au（銅-金）二元系合金のTEM回折パターンをシミュレーションします。特に、特定の原子配列によってのみ現れる「超格子反射」に着目し、その出現メカニズムと強度について理論計算で明らかにします。シミュレーションから、構成原子の種類の違い（原子散乱因子の差）が超格子反射の強度を大きく左右することを示します。

Keywords: 第一原理計算, TEM, 電子回折, 規則合金, Cu-Au, 超格子反射, 構造因子, Pymatgen

TEM回折パターンの原理#

TEM回折パターンを理解するためには、まず「電子が波の性質を持つ」ことと、「結晶が規則的な原子の配列でできている」という2つの基本を理解する必要があります。

ブラッグ回折: 試料に入射した電子の波は、結晶中の規則正しく並んだ原子の面（格子面）によって散乱・反射されます。特定の角度で入射した波は、各格子面で反射された波と強め合い、特定の方向にだけ強い回折波として進みます。この現象がブラッグ回折です。
回折パターンと逆格子空間: TEMのレンズ系は、これらの回折波を蛍光スクリーン上に集め、点状のパターン（回折スポット）として映し出します。この回折パターンは「逆格子空間」と呼ばれる仮想的な空間の一断面を直接反映したものであり、原子レベルの構造情報を持っています。
- 中心の点（透過波）: 回折されずにまっすぐ透過してきた電子のスポットです。
- 周りの点（回折波）: 結晶格子によって回折された電子のスポットです。
- スポット間の距離: 実際の結晶の格子面間隔が「狭い」ほど、回折パターンのスポット間隔は「広く」なります（逆数の関係）。
- パターンの対称性: 結晶そのものの対称性を反映しています。

計算手法#

本解析は、以下の2段階の手順で行いました。

第一原理シミュレーションによる結晶構造の決定: まず、第一原理計算ソフトウェアAdvance/PHASEを用いて、Cu, Au, およびCu-Au金属間化合物（Cu₃Au, CuAu, CuAu₃）の最も安定な結晶構造を精密に決定しました。このステップは、正確な回折パターンを得るための基礎となります。各物質の結晶構造は、先行の解析 [1] で既に決定済みのものを使用しました。
TEM回折パターンの計算: 次に、上記で得られた結晶構造データを、Advance/PHASEのGUIと連携しているPythonの材料科学ライブラリであるPymatgen [2] のTEMCalculatorに入力し、TEM回折パターンをシミュレーションしました。図1はTEM回折パターン計算に用いたGUIの例を示します。

シミュレーションの理論的背景#

本シミュレーションで用いているPymatgenの計算エンジンは、運動学的回折理論に基づいています。この理論は、電子は結晶内で一度だけ散乱されるという理想的な状況を仮定したもので、回折強度 $I$ は構造因子 $F_{hkl}$ の絶対値の二乗に比例します（ $I \propto |F_{hkl}|^2$ ）。構造因子は、結晶格子内の各原子からの散乱波を足し合わせたものであり、原子の配置（座標）と種類（原子散乱因子）によって一意に決まります。

このアプローチにより、第一原理計算で決定された原子レベルの構造情報から、実験で観測される回折パターンを理論的に再現し、その起源を直接結びつけて解釈することが可能となります。ただし、このモデルは試料が非常に薄いという仮定に基づいているため、本シミュレーションで得られる強度は、主に定性的・半定量的な傾向を議論するためのものとなります。

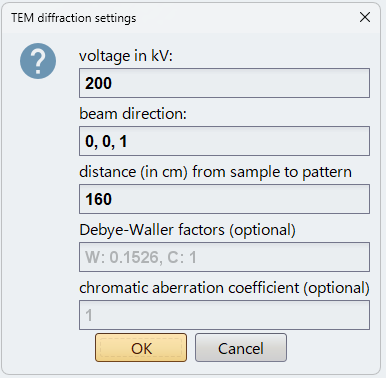
$TEM diffraction settings GUI$

図1.　TEM回折パターン計算に用いたGUIの例。

計算条件#

TEM回折パターンのシミュレーションで用いた主な計算条件を表1に示します。

表1.　計算条件

項目	設定
電圧	200 kV
電子入射方向	[001]
試料-パターン間距離	160 cm

計算結果と考察#

各結晶の回折パターン#

図2に純金属であるCuとAuの計算結果を示します。両者ともFCC（面心立方格子）構造に特徴的な正方格子状の回折パターンを示しています。AuはCuよりも格子定数が大きいため、逆格子空間ではスポットの間隔が狭くなっていることが確認できます。

$TEM diffraction patterns for Cu and Au$

図2.　Cu（左）とAu（右）のTEM回折シミュレーション結果。電子ビームの入射方向は[001]。

次に、CuとAuが1:1で規則的に配列したCuAu（L1₀構造）のパターンを図3に示します。これは純金属のFCC構造とは明らかに異なるパターンであり、結晶構造の変化を鋭敏に反映していることがわかります。

$TEM diffraction pattern for CuAu$

図3.　CuAu (L1₀構造) のTEM回折パターン。(左) pymatgenによる計算結果。(右) コントラストを調整したパターン。

超格子反射の出現#

図4と図5にCu₃AuとCuAu₃（共にL1₂構造）の回折パターンを示します。これらは一見するとFCCのパターンに似ていますが、よく見るとFCCの強い回折スポット（基本反射）の間に、より弱いスポットが現れていることがわかります。この弱いスポットは「超格子反射」と呼ばれ、Cu原子とAu原子がランダムに混在するのではなく、特定のサイトを占有して規則的に配列している（規則構造を形成している）ことの直接的な証拠です。

基本反射: 明るい白色の斑点。これは結晶の基本的な格子構造（この場合はFCC）に由来する強い反射です。FCCの場合、ミラー指数(hkl)がすべて偶数、またはすべて奇数になります。例: (200), (220), (111)。
超格子反射: 暗い灰色の斑点。これはCu原子とAu原子の規則配列によってのみ現れる弱い反射です。ミラー指数が偶数と奇数が混ざったものになります。例: (100), (110), (210)。

$TEM diffraction patterns for Cu3Au$

図4.　Cu₃AuのTEM回折パターン。基本反射の間に、規則構造を示す超格子反射（弱いスポット）が確認できます。(左) pymatgenによる計算結果。(右) コントラストを調整したパターン。

$TEM diffraction patterns for Cu3Au and CuAu3$

図5.　CuAu₃のTEM回折パターン。基本反射の間に、規則構造を示す超格子反射（弱いスポット）が確認できます。(左) pymatgenによる計算結果。(右) コントラストを調整したパターン。

超格子反射の強度比較#

図4と図5を比較すると、Cu₃Auに比べてCuAu₃の超格子反射が相対的に弱いことがわかります。この違いをより明確にするため、回折強度をスポットの大きさで表現しました（図6）。

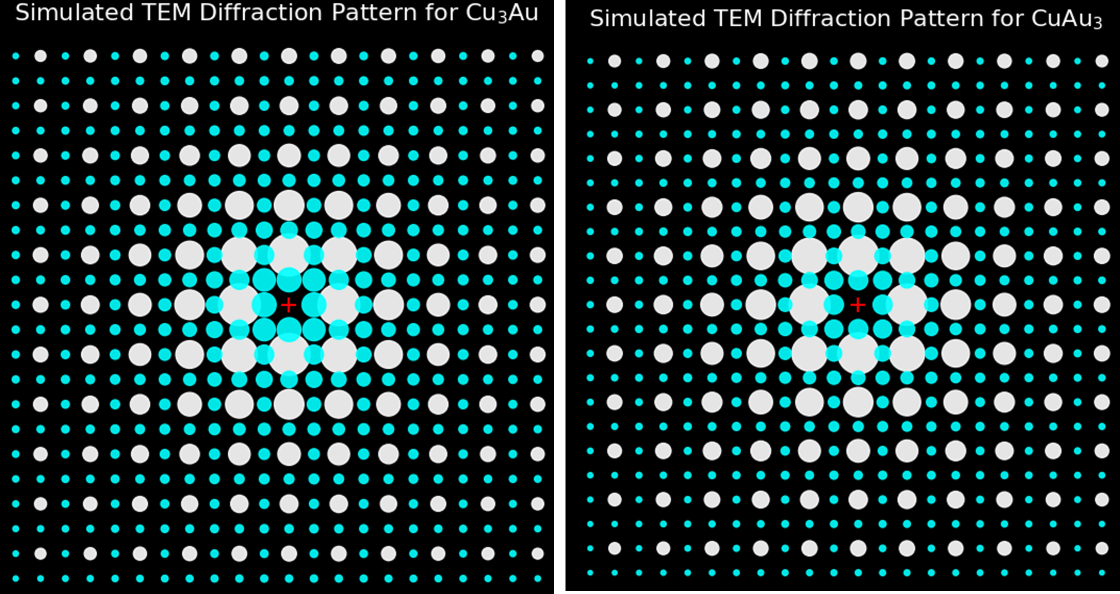
$Simulated TEM diffraction patterns for Cu3Au and CuAu3 with intensity scaling$

図6.　回折強度を斑点のサイズで可視化したCu₃Au（左）とCuAu₃（右）の回折パターン。白い斑点が基本反射、水色の斑点が超格子反射、中心の赤い十字が透過波を示します。CuAu₃の超格子反射が相対的に弱いことがわかります。

考察：CuAu₃における超格子反射の相対強度の低下#

回折強度 $I$ は構造因子 $F$ の絶対値の2乗に比例します（ $I \propto |F|^2$ ）。L1₂構造(組成AB₃)において、基本反射の構造因子 ( $F_{\text{base}}$ ) は構成原子の原子散乱因子 $f$ の加重和で、超格子反射の構造因子 ( $F_{\text{super}}$ ) はその差で与えられます。

$F_{\text{base}} = f_A + 3f_B, \quad F_{\text{super}} = f_A - f_B$

超格子反射の相対強度比 $I_{\text{super}}/I_{\text{base}}$ は、 $|F_{\text{super}}|^2 / |F_{\text{base}}|^2$ に比例します。この比の分子 $|f_{\text{Au}} - f_{\text{Cu}}|^2$ はCu₃AuとCuAu₃で共通です。しかし、分母は異なります。

$\text{Cu}_3\text{Au: } |F_{\text{base}}|^2 = |f_{\text{Au}} + 3f_{\text{Cu}}|^2$ $\text{CuAu}_3\text{: } |F_{\text{base}}|^2 = |f_{\text{Cu}} + 3f_{\text{Au}}|^2$

原子散乱因子は原子番号の大きいAu ( $f_{\text{Au}}$ ) の方がCu ( $f_{\text{Cu}}$ ) より大きいため、CuAu₃の分母はCu₃Auのそれよりも大きくなります。結果として、CuAu₃における超格子反射の相対強度はCu₃Auに比べて明らかに低下します。

まとめ#

本解析では、第一原理計算とTEM回折シミュレーションを組み合わせ、Cu-Au系規則合金の結晶構造と回折パターンの関係を明らかにしました。シミュレーションにより、回折パターンがFCC、L1₀、L1₂といった結晶構造の違いを鋭敏に反映することを確認しました。また、Cu₃AuやCuAu₃などの規則合金では原子の規則配列を直接示す「超格子反射」が現れることも確かめられました。さらに、構造因子の観点から、構成原子の散乱能と化学量論が回折強度に与える影響を定量的に解明し、CuAu₃の超格子反射がCu₃Auに比べて相対的に弱くなる物理的なメカニズムを示しました。このように、第一原理計算に基づくシミュレーションは、実験で得られる複雑なTEM回折パターンを解釈し、その背後にある物理的なメカニズムを原子・電子レベルで深く理解するための強力なツールとなります。

参考文献#

Cu-Au二元系金属間化合物のConvex Hullと熱力学的安定性の第一原理計算
S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. Chevrier, K. A. Persson, and G. Ceder, "Python Materials Genomics (pymatgen) : A Robust, Open-Source Python Library for Materials Analysis", Comp. Mater. Sci. 68, 314 (2013).
D. B. Williams and C. B. Carter, "The Transmission Electron Microscope", In: Transmission Electron Microscopy, Springer, Boston, MA, 1996.