Cu-Au二元系金属間化合物のConvex Hullと熱力学的安定性の第一原理計算#

PHASE logo

Cu-Au（銅-金）合金は、規則-不規則相転移を示す最も代表的な二元系合金であり、合金理論のモデルケースとして古くから研究されてきました。この系では、特定の組成比（Cu₃Au, CuAu, CuAu₃）で原子が規則的に配列した金属間化合物が形成されます。これらの相がどの程度安定であるかを正確に評価することは、材料の熱的挙動を理解し、新しい合金を設計する上で極めて重要です。本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、Cu-Au系の主要な金属間化合物の0 Kにおける生成エンタルピーを計算し、Convex Hull（凸包）を用いて熱力学的な安定性を評価します。

Keywords: 第一原理計算, 生成エンタルピー, 合金, 金属間化合物, Convex Hull, 準安定相, Cu-Au

計算モデルと計算条件#

本解析では、Cu-Au系の代表的な3つの金属間化合物、Cu₃Au, CuAu, CuAu₃の結晶構造をモデル化しました。それぞれの構造を図1に示します。

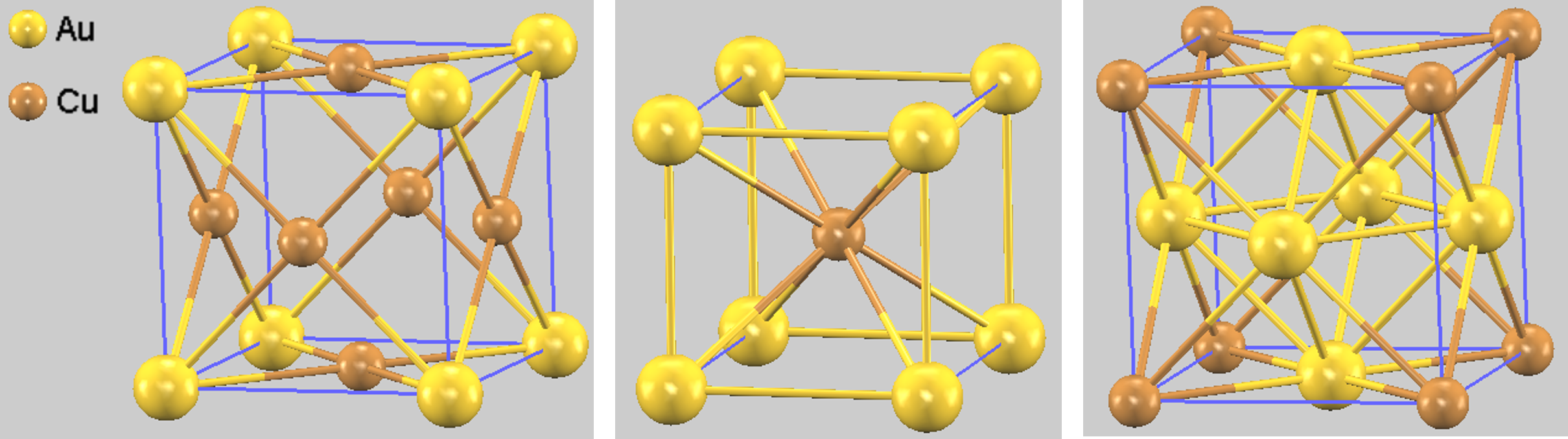
Cu-Au alloy crystal structures

図1.　計算に用いたCu-Au系金属間化合物の結晶構造。(左から) Cu₃Au (L1₂構造, cubic), CuAu (L1₀構造, tetragonal), CuAu₃ (L1₂構造, cubic)。

本解析で用いた主な計算条件は表1に示されています。交換相関汎関数には、固体の構造特性（格子定数など）を高精度に再現することを目的に開発されたPBEsolを採用しました。k点サンプリングは、形成エンタルピーのような微小なエネルギー差を高精度に計算するため、逆格子空間におけるサンプリング密度が全ての計算で等価になるように設定しました。具体的には、fcc Au格子における8x8x8メッシュと等価な密度を持つk点メッシュを基準としています。また、カットオフエネルギーについてエネルギー計算とストレステンソルを用いた計算には、十分な収束性を確認した値を採用しました。

表1.　計算条件の概要

項目	設定
擬ポテンシャル	PAWポテンシャル
交換相関汎関数	GGA (PBEsol)
k点サンプリング	等価なk点密度（fcc Auの8x8x8メッシュ相当）

計算結果と考察#

格子定数の計算結果#

各構造について、原子位置と格子定数を完全に最適化しました。計算で得られた格子定数と実験値を比較して表2にまとめます。

表2.　計算で得られた格子定数と実験値の比較

化合物	計算値 (Å)	実験値 (Å)
Cu₃Au	a = 3.723	a = 3.747 [1]
CuAu	a = b = 2.796, c = 3.651	a = b = 2.802, c = 3.671 [2]
CuAu₃	a = 3.974	a = 3.965 [1]

計算で得られた格子定数は、実験値と1%未満の誤差で非常によく一致しており、本計算の精度の高さを示しています。

生成エンタルピーの計算#

合金の熱力学的な安定性は、生成エンタルピー（ΔH_form）によって評価されます。これは、合金がその構成元素（この場合は純粋なCuとAu）から形成される際のエネルギー変化量であり、0 Kにおける安定性の指標となります。負の値が小さいほど、その合金が安定であることを意味します。

計算式:

合金 Cu_1-xAu_x の1原子あたりの生成エンタルピーは、以下の式で計算されます。

ΔH_form = E_alloy - (1-x) * E_Cu - x * E_Au

ここで、E_alloy, E_Cu, E_Auはそれぞれ合金、純Cu、純Auの1原子あたりの全エネルギーです。xはAuの組成比です。

計算した各合金の生成エンタルピーを表3にまとめ、実験値と比較します。

表3.　PBEsolによる生成エンタルピー (0 K) と実験値 (320 K) の比較

Alloy	PBEsol 計算値 (eV/atom)	実験値 (eV/atom) [3]
Cu₃Au	-0.0542	-0.074
CuAu	-0.0710	-0.093
CuAu₃	-0.0333	-0.039

表3の結果から、PBEsolによる計算値は実験値の傾向を定性的に正しく再現していることがわかります。特に、3つの化合物の中ではCuAuが最も安定であるという序列も一致しています。ただし、計算値は絶対零度(0 K)のものであるのに対し、実験値は320 Kのものであり、熱振動などの影響が含まれるため、値が完全に一致しないのは妥当です。一般に、PBEsolのようなGGA汎関数は貴金属を含む合金の結合エネルギーを過小評価する傾向があり、今回の計算結果もそれに沿ったものと考えられます。

Convex Hullによる熱力学的安定性評価#

個々の化合物の安定性だけでなく、異なる組成の相との競合を含めた全体的な安定性を評価するために、Convex Hull（凸包）を描画します。

Convex Hullの描き方:

横軸をAuの組成比、縦軸を生成エンタルピーとして、純金属（両端の0 eV）と計算した全ての合金の点をプロットします。
プロットした全ての点の下側を通るように、最もエネルギーが低い点を直線で結びます。この下側の包絡線がConvex Hullであり、全データ点の下側に輪ゴムをかけたような線とイメージできます。
Convex Hull上に乗っている相が、熱力学的に安定な基底状態です。線より上にある相は、より安定な相の組み合わせに分解する可能性がある不安定相または準安定相です。

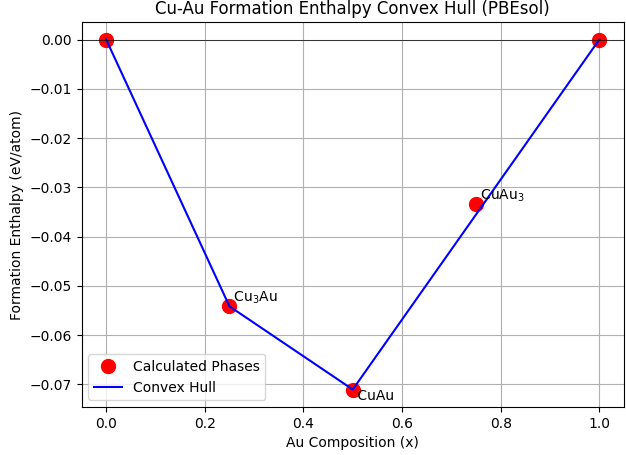
Cu-Au Formation Enthalpy Convex Hull (PBEsol)

図2.　PBEsolの計算結果から作成したCu-Au系のConvex Hull図。

図2から、Cu₃AuとCuAuはConvex Hull上に位置しており、0 Kにおいて熱力学的に安定な化合物であることが分かります。一方、CuAu₃はConvex Hullよりもわずかに上側に位置しており、最も安定な状態ではないことが示唆されます。

準安定相の評価：分解の駆動力#

Convex Hull上にない相が、より安定な相へと分解しようとする力の大きさを「分解の駆動力」と呼びます。これは、その相のエネルギーと、同じ組成におけるConvex Hull上のエネルギーとの差として定量化できます。

分解の駆動力の計算:

CuAu₃ (x=0.75) は、安定な相であるCuAu (x=0.5) と Au (x=1.0) の間に位置します。この2点を結ぶ直線（Convex Hull）のx=0.75におけるエネルギー E_hull は、線形補間で求められます。

分解の駆動力 E_d = ΔH(CuAu₃) - E_hull(x=0.75)

CuAu₃の分解の駆動力は +2.2 meV/atom と計算されました。この値は、第一原理計算の典型的な誤差（数meV/atom）の範囲内であり、室温での熱エネルギー kT（約25 meV）と比較しても1桁小さく、非常に小さい値です。これは、CuAu₃が熱力学的な真の基底状態ではないものの、エネルギー的な不利がごくわずかであり、分解するための駆動力が極めて小さいことを意味します。このような相は「準安定相」と呼ばれ、原子の拡散が抑制される低温では、分解せずに長時間存在し続けることができます。この計算結果は、実験的にCuAu₃相が観測される事実と整合的です。実際、CuAu₃の安定性については、Ozoliņšらによる詳細な第一原理計算研究 [4] においても、一般的に知られるL1₂構造は真の基底状態ではなく、(100)方向に積層した別の超格子構造がより安定であると理論的に予測されています。本計算で得られた+2.2 meV/atomという非常に小さな分解の駆動力は、L1₂構造のCuAu₃がなぜエネルギー的に不利でありながら、準安定相として実験的に観測されうるのかを定量的に裏付ける結果と言えます。

まとめ#

本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、Cu-Au二元系の主要な金属間化合物（Cu₃Au, CuAu, CuAu₃）の熱力学的安定性を評価しました。交換相関汎関数PBEsolを用いた計算により、実験値とよく一致する格子定数を得ました。生成エンタルピーとConvex Hull解析の結果、Cu₃AuとCuAuは0 Kで安定な基底状態であることが示されました。CuAu₃はConvex Hullからわずか+2.2 meV/atomだけ不安定であり、これは実験で観測される事実を説明する「準安定相」として存在しうることを示唆しています。本解析は、第一原理計算が合金の相安定性を定量的に評価し、準安定相の存在可能性といった複雑な熱力学的挙動を解明するための強力なツールであることを示しています。

参考文献#

H. S. Lu and C. K. Liang, "The superlattice formation and lattice spacing changes in copper-gold alloys (English Translation)", Chinese J. Phys. 22, 505 (1966).
E. Bjerkelund, W. B. Pearson, K. Selte, and A. Kjekshus, "Lattice Parameters of the CuAu(I) Phase", Acta Chemica Scandinavica 21, 2900 (1967).
R. L. Orr, "Heats of formation of solid Au-Cu alloys", Acta Metallurgica 8, 489 (1960).
V. Ozoliņš, C. Wolverton, and A. Zunger, "Cu-Au, Ag-Au, Cu-Ag, and Ni-Au intermetallics: First-principles study of temperature-composition phase diagrams and structures", Phys. Rev. B 57, 6427 (1998).