ショットキーバリア高さの第一原理計算とTCADの連携：内蔵電界と電流特性の解析#

Advance/PHASE Logo

パワー半導体デバイスの設計において、金属/半導体界面のショットキーバリア高さ（SBH）は、立ち上がり電圧やリーク電流、耐圧を決定づける極めて重要なパラメータです。従来、SBHは実験値のフィッティングにより決定されてきましたが、第一原理計算（DFT）を用いることで、金属種や界面原子構造に依存した固有の値を予測することが可能です。本事例では、Advance/PHASEを用いたDFT計算により算出されたCuと4H-SiC界面のSBHを用いて、Pythonベースの1次元デバイスシミュレータ（自作TCADソルバー）と連携させ、デバイス内部の電界分布やI-V特性に与える影響を定量的に評価しました。

Keywords: 第一原理計算（DFT）, TCAD連携, SiC, ショットキーバリアダイオード(SBD), 内蔵電界, I-V特性, Python数値解析

1. 計算手順#

Step 1: 第一原理計算によるp型SBHの算出と検証#

まず、Advance/PHASEを用いて Cu/4H-SiC 界面の電子状態計算を行いました。界面モデルとして $\sqrt{3} \times \sqrt{3}$ 構造を採用し、p型ショットキーバリア高さ（ $\Phi_{Bp}$ ）を算出しました [1]。

表1. 計算結果と実験値の比較（検証フェーズ）

系 (System)	計算値 (DFT)	実験値（経験則）[2]
Cu / 4H-SiC (p-type)	1.80 eV	1.74 eV

実験的傾向（Trend）との整合性検証

Leeらの研究 [2] によれば、p型4H-SiCのSBHは金属仕事関数（ $\Phi_m$ ）に対して以下の線形関係に従うことが報告されています。

$\Phi_{Bp} = 4.58 - 0.61 \Phi_m$

この実験式にCuの仕事関数（約 4.65 eV）を代入すると、予測値は 1.74 eVとなります。本事例の計算値（1.80 eV）はこの予測値と非常によく一致しており、特定の実験点との一致だけでなく、物理的な傾向（傾き）も正しく再現していることが確認されました。

Step 2: バンドギャップを用いたn型SBHへの換算#

パワーデバイスとして広く用いられるのはn型半導体です。そこで、検証済みのp型SBHと、4H-SiCの実験バンドギャップ（ $E_g$ ）を用いて、n型ショットキーバリア高さ（ $\Phi_{Bn}$ ）を導出しました。

$\Phi_{Bn} = E_g - \Phi_{Bp}$

ここで、 $E_g = 3.25 \text{ eV}$ （4H-SiCの代表的な実験値 [3]）とすると、以下のようになります。

$\Phi_{Bn} = 3.25 \text{ eV} - 1.80 \text{ eV} = \mathbf{1.45 \text{ eV}}$

この値は、単純な理想界面モデル（Schottky-Mott則）では予測困難な、現実の界面準位や原子再配列の影響を考慮した、より現実的な値と言えます。

Step 3: Pythonソルバーによる簡易デバイスシミュレーション#

得られたSBHを境界条件として入力し、Pythonで実装した1次元ポアソン方程式ソルバーを用いて、ショットキーバリアダイオード（SBD）の電気的特性を計算しました。これにより、第一原理計算の結果がデバイス特性に及ぼす影響を迅速に確認しました。

2. TCADシミュレーションにおける支配方程式と計算モデル#

計算対象デバイス構造#

本解析で対象とするショットキーバリアダイオード（SBD）の構造図を図1に示します。DFT計算で得られた界面特性を「Schottky Anode」の境界条件として適用し、深さ方向の1次元解析を行いました。

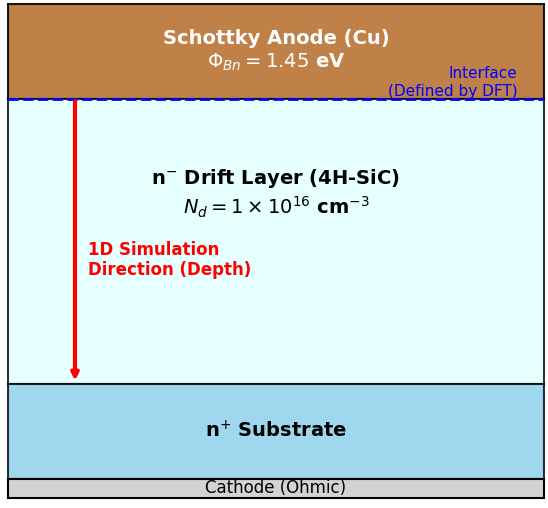
SBD Device Structure Schematic
図1. 解析対象のSiC SBDデバイス構造模式図。DFT計算で得られたSBHを境界条件として設定。n^- : 低濃度ドープn型半導体（ドリフト層）、n⁺: 高濃度ドープn型半導体（基板）。

ポアソン方程式（電位・電界分布）#

半導体内部の静電ポテンシャル $\phi(x)$ 分布は、以下の非線形ポアソン方程式によって記述されます [4]。本解析では、完全空乏層近似（Full Depletion Approximation）を用いた解析モデルにより、ポアソン方程式の解を導出しました。

$\frac{d^2 \phi}{dx^2} = -\frac{q}{\epsilon_s} \left( N_d - N_c \exp\left(\frac{q(\phi - \phi_{ref})}{k_B T}\right) \right)$

ここで、 $\epsilon_s$ はSiCの誘電率、 $N_d$ はドナー濃度、 $N_c$ は伝導帯有効状態密度です。電子密度はボルツマン統計に従うと仮定しています。

境界条件（DFT連携の核心）#

第一原理計算の結果は、界面（ $x=0$ ）におけるディリクレ境界条件として組み込まれます。

$\phi(0) = -\Phi_{B(\text{DFT})} + V_{\text{bias}}$

この境界条件により、原子レベルの電子状態の計算結果が、デバイス全体の内蔵電位差およびバンドの曲がり具合を決定します。

電流密度式（熱電子放出モデル）#

I-V特性の計算には、ショットキー接合における支配的な輸送機構である熱電子放出（Thermionic Emission）理論を用いました [4]。

$J = A^* T^2 \exp\left(-\frac{q \Phi_{B(DFT)}}{k_B T}\right) \left[ \exp\left(\frac{q V}{n k_B T}\right) - 1 \right]$

$A^*$ はリチャードソン定数、 $n$ は理想係数です。SBH $\Phi_B$ が指数関数の肩に乗るため、わずかなSBHの差が電流値のオーダー（桁）に影響します。

表2. デバイスシミュレーション計算条件

パラメータ	設定値	備考
解析対象	4H-SiC SBD (n型)	Si面終端
ドナー濃度 ( $N_d$ )	$1.0 \times 10^{16}$ cm^-3	ドリフト層
温度 ( $T$ )	300 K	室温
伝導帯有効状態密度 ( $N_c$ )	$1.7 \times 10^{19}$ cm^-3	4H-SiC (300K) の代表値 [3]
誘電率 ( $\epsilon_r$ )	9.7	4H-SiC
SBH ( $\Phi_B$ )	Cu: 1.45 eV	DFT計算値
リチャードソン定数 ( $A^*$ )	$146.0 \text{ A/cm}^2\text{K}^2$	4H-SiC理論値 [5] ※ 伝導帯有効質量に基づく
理想係数 ( $n$ )	1.05	鏡像力効果等を考慮した理想的な界面状態を想定

3. 解析結果と考察#

導出した $\Phi_{Bn} = 1.45 \text{ eV}$ をPython形式のTCADソルバーに入力し、n型SBDの電気的特性をシミュレーションしました。

3.1 電流-電圧（I-V）特性の予測#

図2に、順方向I-V特性の解析結果（対数スケール）を示します。オン電圧（立ち上がり電圧）の指標として、電流密度 1 A/cm² における電圧値を確認しました。

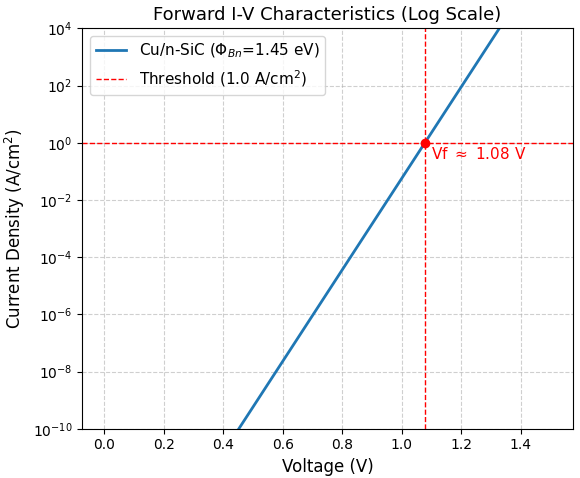
Derived n-type I-V Characteristics (Log Scale)
図2. 導出されたn型SBH (1.45 eV) に基づくCu/n-SiC SBDのI-V特性予測（対数スケール）。電流密度 1 A/cm² における順方向電圧は、約 1.08 V と予測されています。

また、立ち上がり特性をより直感的に確認するため、線形スケールで表示したものを図3に示します。

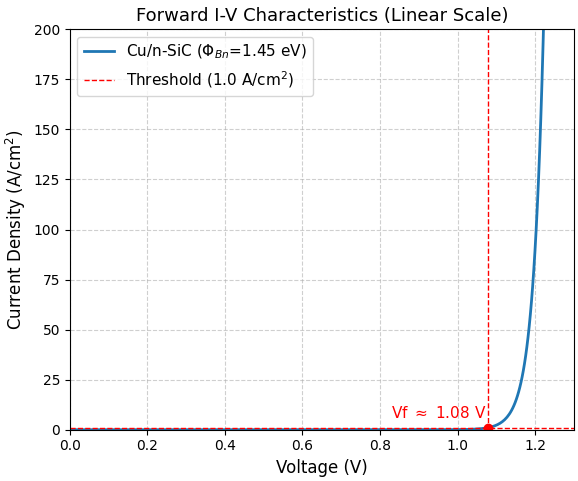
Derived n-type I-V Characteristics (Linear Scale)
図3. 線形スケールで表示した順方向I-V特性。約 1.08 V 付近で電流が急激に立ち上がる様子（Knee電圧）が確認できます。

考察と実験事実との整合性：

本シミュレーションでは立ち上がり電圧の指標として 1 A/cm² での値を予測しましたが、実験値との直接的な比較を行うため、以下では文献 [6] に実測データが記載されている電流密度 100 A/cm² の条件を用いて評価します。

実験値との比較: 電流密度 100 A/cm² における本解析の Cu SBD の順方向電圧は、約 1.2 V と予測されます。これは、文献 [6] で報告している 4H-SiC 上の実験値（Ti: 1.12 V, Ni: 1.50 V @ 100 A/cm²）の範囲内にあり、かつ両者の中間に位置します。この結果は、金属仕事関数の序列（Ti < Cu < Ni）に従う物理的に妥当な挙動であり、シミュレーションの信頼性を裏付けるものです。
特性バランスの優位性: 導出された Cu のバリア高さ（1.45 eV）は、低損失重視の Ti よりも十分に高く、低電圧領域でのリーク電流を大幅に抑制可能です。一方で、高耐圧重視の Ni よりも低いオン電圧（100 A/cm² 時点で Ni より約 0.3 V 低い）を示すため、Cu 電極は「低損失」と「低リーク」のトレードオフを解消するバランスの取れた材料候補であることが定量的に示唆されました。

3.2 バンドプロファイルと電界分布#

次に、ゼロバイアス時における伝導帯（ $E_c$ ）のバンドプロファイル（空間分布）と、内部電界分布を解析しました（図4）。

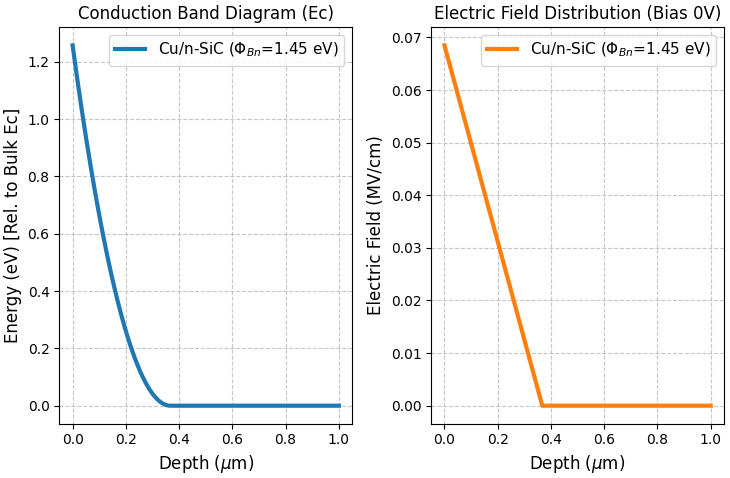
Band Diagram and Electric Field for n-type
図4. Cu/n-SiC界面近傍の伝導帯バンドプロファイル（左）と内蔵電界分布（右）。

解析結果：

バンドベンディング（図4左）： 界面においてバンドが約 1.27 eV ( $\approx \Phi_{Bn} - \text{Potential}_{\text{bulk}}$ ) 持ち上がっており、電子に対する高い障壁が形成されています。
電界分布（図4右）： バンドの曲がりに対応して、界面で最大電界（約 0.069 MV/cm）が発生しています。この内蔵電界の値は、逆バイアス印加時のアバランシェ降伏の起点となるため、耐圧設計において重要な指標となります。

より複雑・現実的なデバイス設計へ

上記のPythonソルバーによる解析は、物理現象の理解やプロトタイピング（Concept Proof）に最適です。しかし、実際のデバイス開発では、3次元構造、複雑な不純物分布、高電圧下でのアバランシェ降伏などを考慮する必要があります。これらの高度な解析には、統合TCADシステム「Advance/TCAD」のような専用ソフトウェアの使用が推奨されます。

まとめ#

本事例では、第一原理計算ソフトウェアAdvance/PHASEを用いた、実験値と整合するDFT計算結果（p型SBH）を出発点とし、バンドギャップ換算を経てn型パワーデバイスの特性予測を行いました。「計算精度検証」→「実用パラメータへの変換」→「デバイスシミュレーション」という一連のフローにより、実験データが乏しい新規材料や界面構造であっても、高精度な特性予測とデバイス設計が可能であることを示しました。

本解析の詳細や、研究への適用可能性に関するご相談はこちら

お問い合わせ

参考文献#

ショットキーバリア高さの第一原理計算
S.-K. Lee, C.-M. Zetterling, and M. Ostling, "Schottky Barrier Height Dependence on the Metal Work Function for p-type 4H-Silicon Carbide", J. Electron. Mater. 30, 242 (2001).
T. Hatakeyama, K. Fukuda, and H. Okumura, "Physical Models for SiC and Their Application to Device Simulations of SiC Insulated-Gate Bipolar Transistors", IEEE Trans. Electron Devices 60, 613 (2013).
S. M. Sze and K. K. Ng, Physics of Semiconductor Devices, 3rd ed., Wiley (2006).
A. Itoh and H. Matsunami, "Analysis of Schottky Barrier Heights of Metal/SiC Contacts and Its Possible Application to High-Voltage Rectifying Devices", Phys. Status Solidi (a) 162, 389 (1997).
A. Itoh, T. Kimoto, and H. Matsunami, "High performance of high-voltage 4H-SiC Schottky barrier diodes", IEEE Electron Device Lett. 16, 280 (1995).