ショットキーバリア高さの第一原理計算#

金属と半導体の界面に形成されるショットキーバリアの高さ（SBH）は、デバイスの電気特性を左右する重要なパラメータです。SBHは界面の微視的な物理現象に強く依存するため、その予測には複雑な電子状態をシミュレーションできる第一原理計算が最も強力な手法の一つです。本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、次世代パワーデバイス材料である炭化ケイ素（4H-SiC）と金属（Al, Cu）の界面におけるSBHを評価します。

Keywords: ショットキーバリア高さ (SBH), 第一原理計算, 金属/半導体界面, 4H-SiC, 層分割局所状態密度 (LayerDOS), バンドベンディング

ショットキーバリア高さの計算方法#

概念：バンドダイアグラムからの理解#

SBHの形成は、バンドダイアグラムを用いると直感的に理解できます。金属と半導体を接触させると、両者のフェルミ準位が一致するように電子が移動します。この際、半導体の種類によってバンドの曲がり（バンドベンディング）の向きが変わります。図1(a)はn型半導体の例で、電子が半導体から金属へ移動し、界面のバンドが上に曲がります。逆にp型半導体の場合は、図1(b)のようにバンドは下に曲がることが一般的です。このバンドの曲がりによって障壁が形成され、その高さは電子に対するn型SBHと、正孔に対するp型SBHとして定義されます。

しかし、第一原理計算で広く用いられるGGA（一般化勾配近似）などの計算手法には、半導体のバンドギャップを実際よりもかなり小さく評価してしまう（過小評価）という課題があります。これにより、価電子帯の上端（VBM）の位置は比較的精度良く求まる一方、伝導帯の下端（CBM）の位置の計算精度が低くなり、CBMを基準とするn型SBHの計算に問題が生じます。このため、本解析のような多くの研究では、より高精度に計算できるVBMを基準としたp型SBHを評価します。

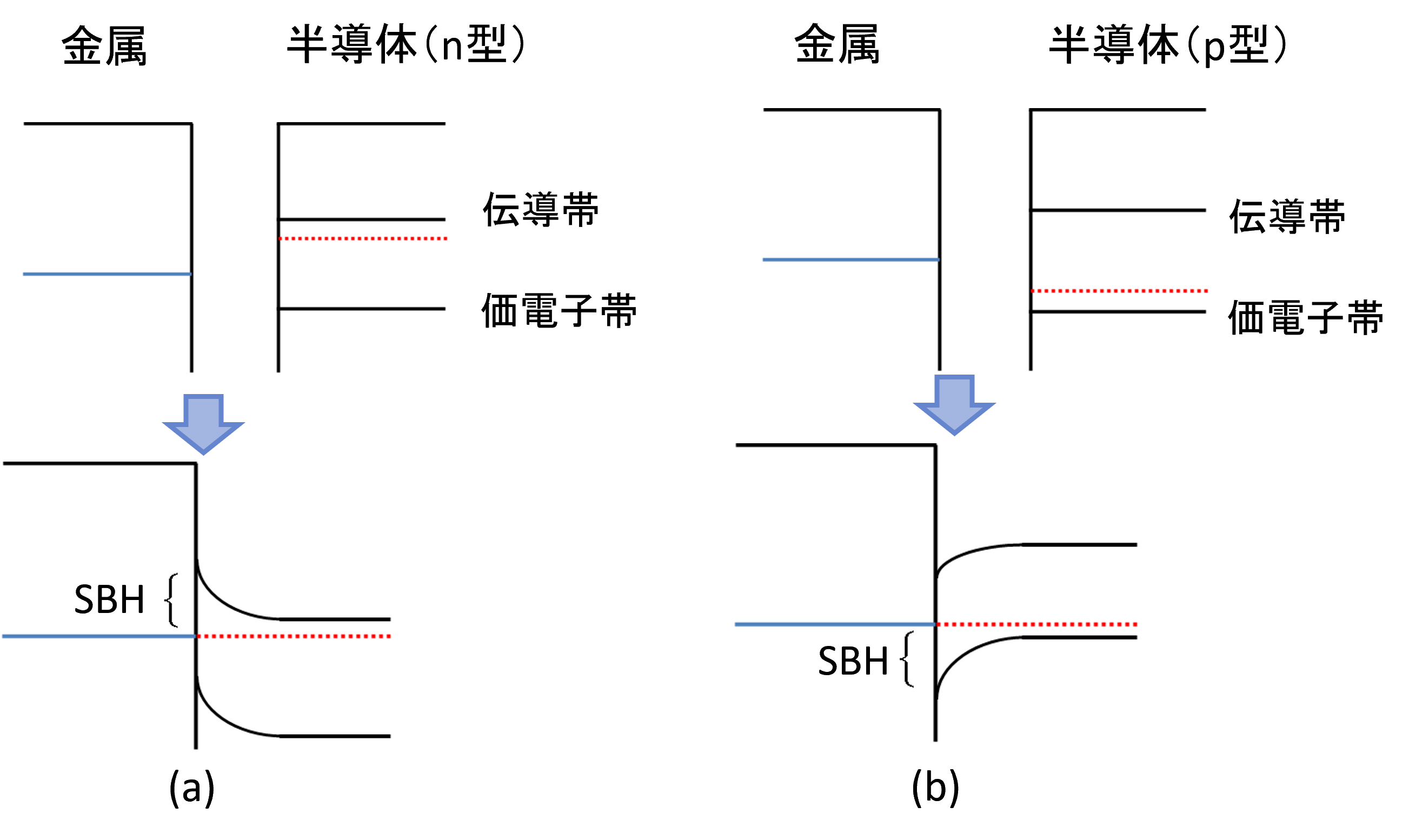
図1.　金属と半導体の接触によるSBH形成の概念図: (a) n型半導体 (b) p型半導体。青線・赤線はそれぞれ金属・半導体のフェルミ準位を示します。

手法：第一原理計算によるSBHの評価#

第一原理計算では、SBHを評価するために主に2つのアプローチがあります。本解析では、そのうち物理的に直感的な直接法を用いていますが、有限サイズ効果を補正するポテンシャルアライメント法との関係性を理解することが重要です。

A. 直接法（本解析でのアプローチ）#

この方法は、十分に厚いスーパーセルモデルを仮定し、以下の手順でSBHを直接的に評価します。

界面モデル構築: 金属と半導体の界面構造をスーパーセルモデルで作成します。このとき、界面から離れている半導体層がバルク（本来の半導体）の性質を十分に反映するよう、層の厚みを確保します。
電子状態計算: 作成したモデルに対して密度汎関数理論（DFT）に基づき、系全体の電子状態を計算します。これにより、接合後の平衡状態におけるフェルミ準位 ( $E_F$ )が決定されます。
VBMの特定: 半導体バルク層の層分割局所状態密度（LayerDOS）を解析し、VBMのエネルギー $E_{VBM}$ を読み取ります。
SBHの算出: 決定したフェルミ準位とVBMから、p型半導体に対するショットキーバリア高さ $\Phi_{SB,p}$ を算出します。 $\Phi_{SB,p} = E_F - E_{VBM}$

このアプローチは、「界面から離れている、界面の影響を受けない真のバルク状態を再現している」という物理的な前提に基づいています。また、図1に示す界面 (device scale)を原子スケールで解析するため、VBMの特定は界面に一番近い原子層ではなく半導体のバルク層で行います。

B. ポテンシャルアライメント法と直接法との関係#

現実の計算ではスーパーセルが有限の厚みしか持たないため、界面の影響を系統的に補正する手法としてポテンシャルアライメント法があります。では、なぜ補正を行わない直接法でも妥当な値が得られるのでしょうか。それは、両者が理想的な条件下では物理的に等価になるためです。

ポテンシャルアライメント法では、アライメントされたVBM（ $E_{\text{VBM, aligned}}$ ）を、別途計算したバルクの性質を用いて以下のように定義します。 $E_{\text{VBM, aligned}} = \langle V \rangle_{\text{interface}} + (E_{\text{VBM, bulk}} - \langle V \rangle_{\text{bulk}})$ ここで、 $\langle V \rangle$ は平均静電ポテンシャルです。一方、理想的な（＝無限に厚い）スーパーセルを考えると、そのバルク層は真のバルクと全く同じ状態になります。これは、VBMと $\langle V \rangle$ の関係が、界面モデルのバルク層とバルク単体で等しくなることを意味します。 $E_{\text{VBM}} - \langle V \rangle_{\text{interface}} = E_{\text{VBM, bulk}} - \langle V \rangle_{\text{bulk}}$ この式を変形すると $E_{\text{VBM}} = \langle V \rangle_{\text{interface}} + (E_{\text{VBM, bulk}} - \langle V \rangle_{\text{bulk}})$ となり、これは $E_{\text{VBM, aligned}}$ の定義と完全に一致します。つまり、理想的な条件が満たされれば、直接法で得られるVBMは、ポテンシャルアライメント法が算出するVBMと等しくなるのです。

計算モデル#

本解析では、4H-SiCの(0001)面（Si終端、C終端）と各種金属を接触させた界面モデルを、(2x2)の周期で作成しました。真空層は10 Å、スラブの下端は水素（H）原子で終端処理されており、バルク層を模擬しています。図2にSi終端面の3種類の界面モデルの原子構造を示します。層分割局所状態密度（LayerDOS）の解析では、金属と直接結合している「界面層」と、界面から離れた「バルク層」の電子状態をそれぞれ評価します。

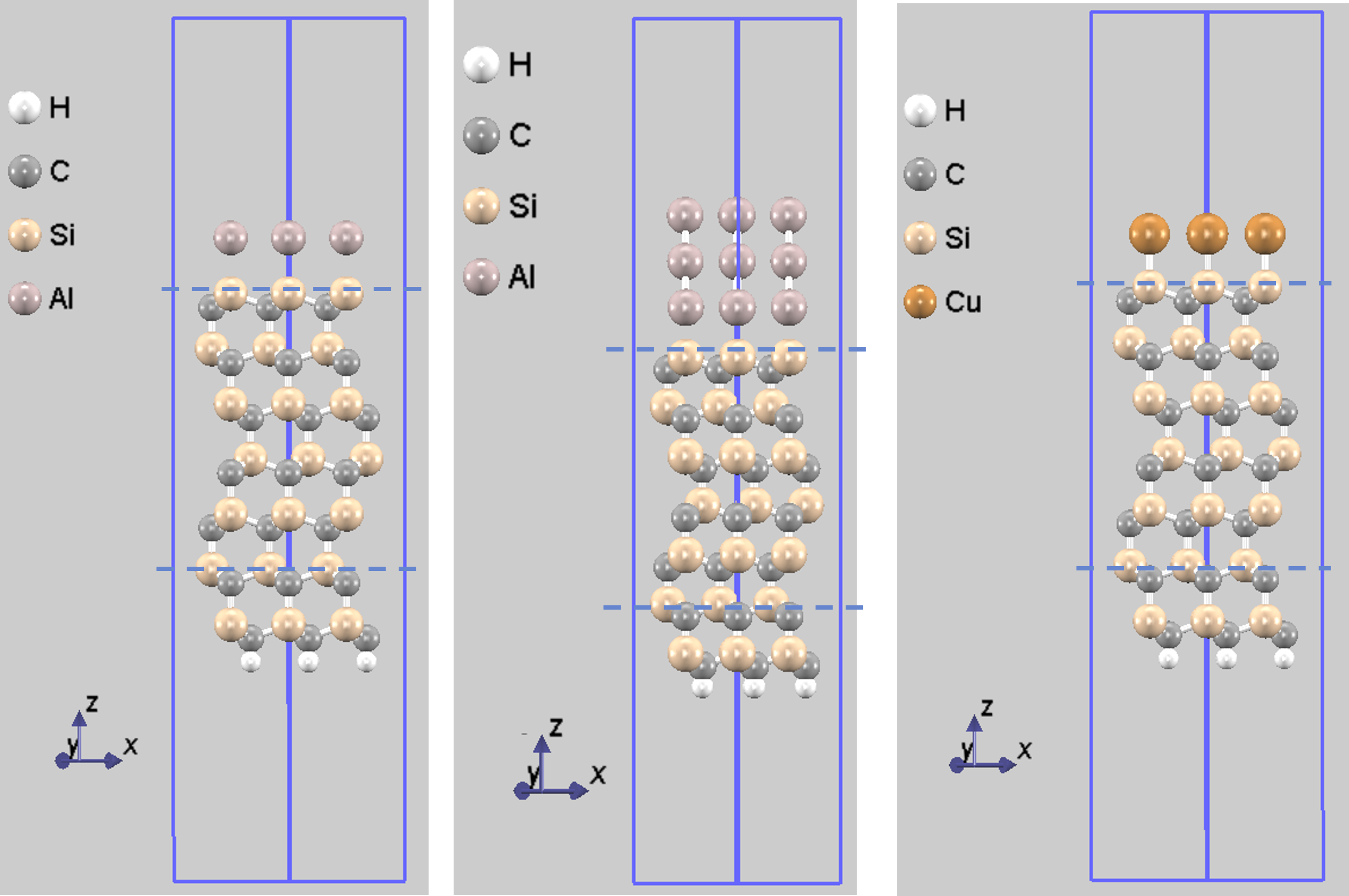
図2.　金属/Si終端面の原子構造モデル（左：Al層1層-(2x2)モデル、中：Al層3層-(2x2)モデル、右：Cu層1層-(2x2)モデル）。点線はそれぞれ、金属に接したSiC層（界面層）と、界面から離れた「バルク層」の位置を示しています。

解析結果と考察#

各モデルについて、界面層とバルク層のLayerDOSを解析し、SBHを評価しました。

Al層1層‐(2×2)モデル#

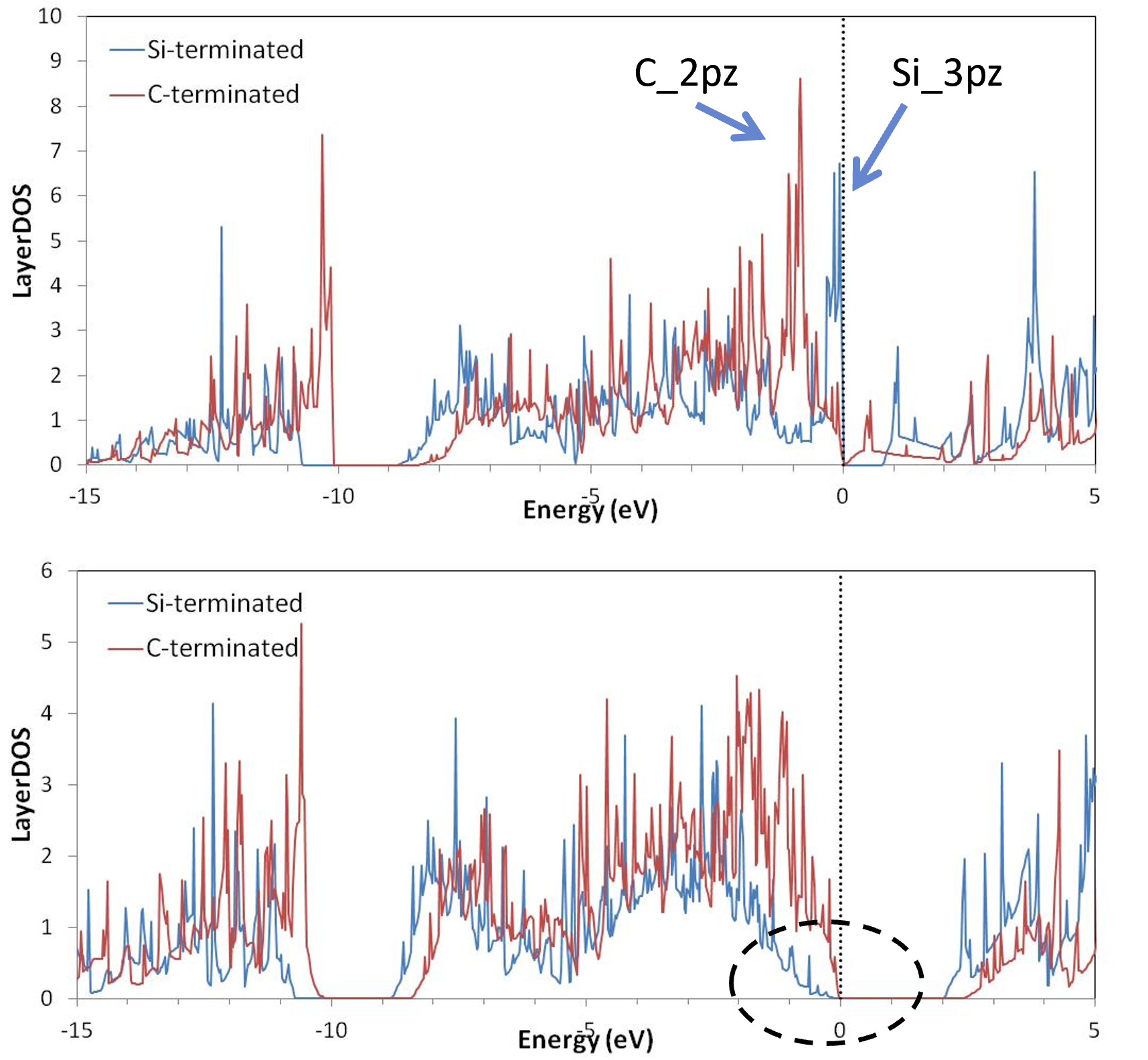
図3.　Al層1層‐(2×2)モデルのLayerDOS（上：界面層、下：バルク層）。フェルミ準位が0 eVに設定されています。

図3に、Al層を1層だけ積層したモデルのLayerDOSを示します。

界面層 (上グラフ): 金属との強い相互作用により、0 eV (フェルミ準位) 近傍に多くの界面準位が形成され、DOSが複雑な形状をしています。C終端面（赤線）では炭素の2pz軌道が、Si終端面（青線）ではケイ素の3pz軌道が、フェルミ準位近傍の界面準位形成に大きく寄与しています。
バルク層 (下グラフ): 界面から離れているため、半導体本来の性質を反映した、明確なバンドギャップを持つDOSが示されます。Si終端面（青線）、C終端面（赤線）のいずれにおいても、VBMがフェルミ準位に非常に近いため、SBHはほぼゼロ（0 eV）になり、これはショットキー特性を示さないオーミック的接触に近い状態が形成されていることを示唆します。

Al層3層‐(2×2)モデル#

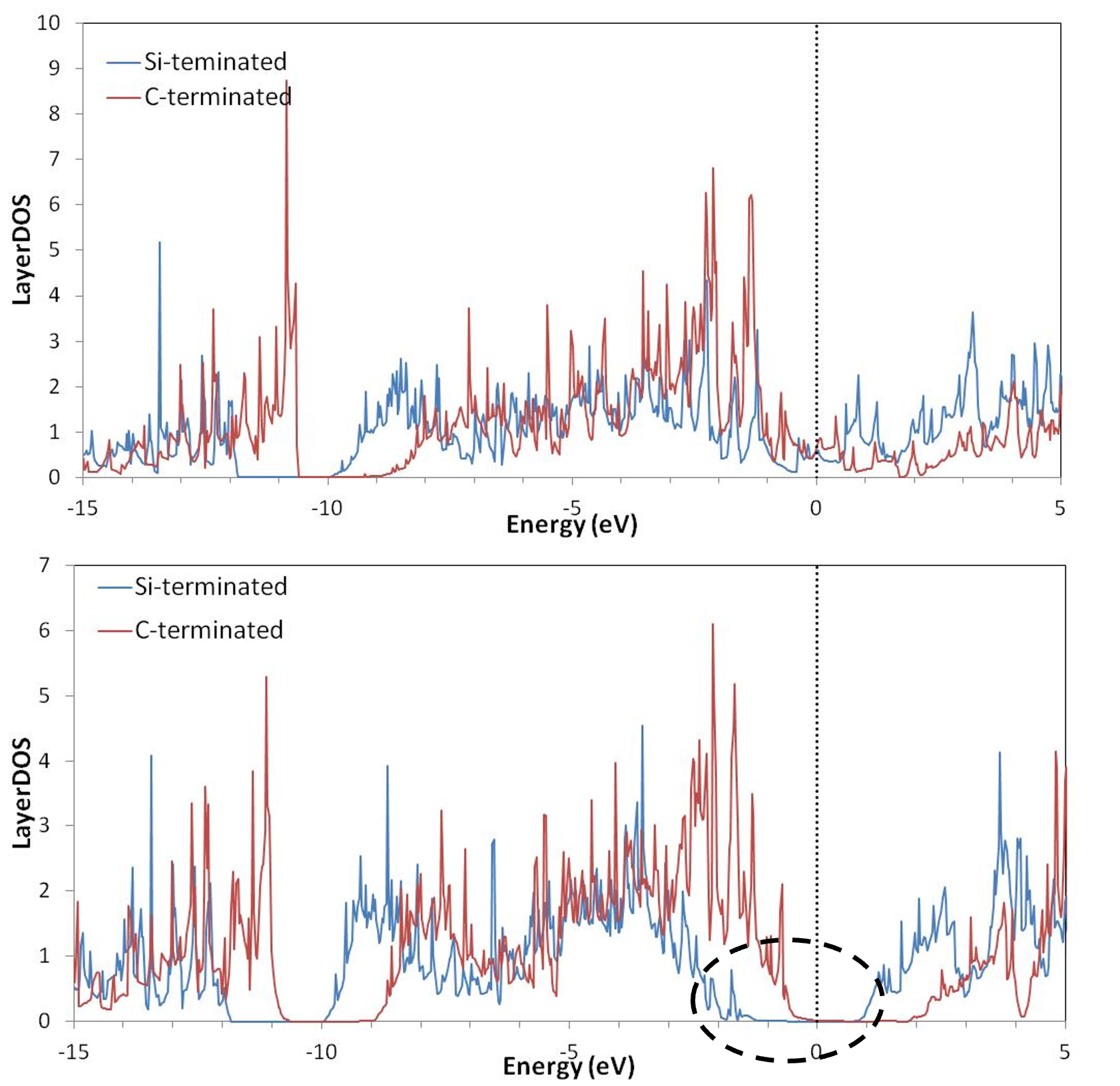
図4.　Al層3層‐(2×2)モデルのLayerDOS（上：界面層、下：バルク層）。フェルミ準位が0 eVに設定されています。

金属層を3層に厚くしたモデルの結果です（図4）。

界面層 (上グラフ): 1層モデルと同様に、0 eV近傍 (フェルミ準位) に多くの界面準位が形成されます。
バルク層（下グラフ）: Si終端面（青線）ではVBMが-1.05 eVにあり、SBHは1.05 eVと計算されています。一方、C終端面（赤線）ではVBMが-0.31 eVにあり、SBHは0.31 eVというオーミック接触に近い特性を示す値となります。実験で報告されているSBH（1.83 eV）は明確なショットキー特性を示すことから、観測された障壁は主にSi終端面に起因すると考えられます。ただし、Si終端面の計算値（1.05 eV）と実験値との間には差が見られ、この乖離はさらに計算に用いた金属層を増やす必要がある可能性を示唆しています。

Cu層1層‐(2×2)モデル#

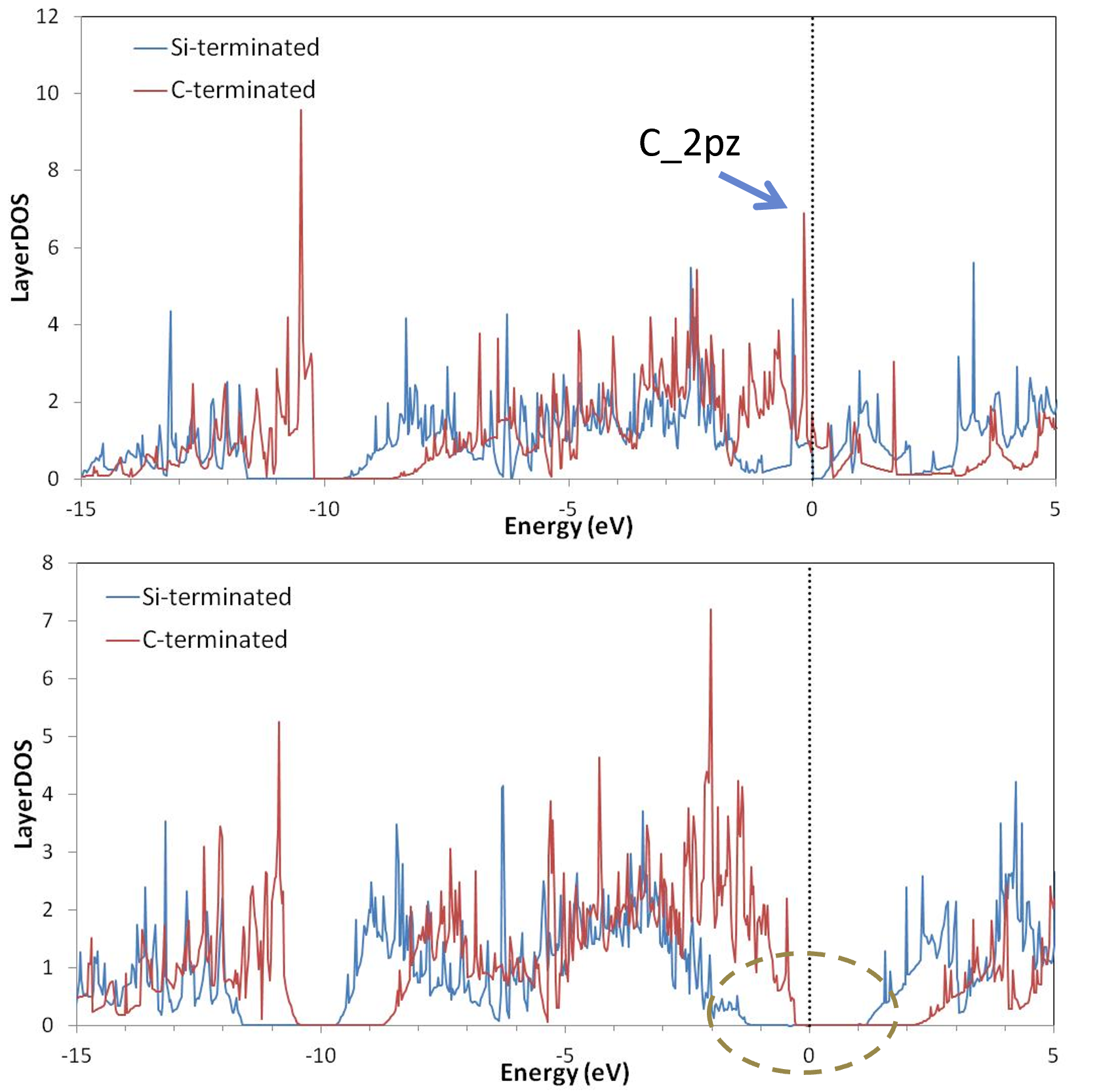
図5.　Cu層1層‐(2×2)モデルのLayerDOS（上：界面層、下：バルク層）。フェルミ準位が0 eVに設定されています。

金属を銅(Cu)に変えた場合の結果です（図5）。

界面層 (上グラフ): ここでも界面準位が0 eV (フェルミ準位) 近傍に現れています。特にC終端面（赤線）では、フェルミ準位近傍の鋭いピークが炭素の2pz軌道に由来することが示されており、炭素原子が界面の電子状態に強く影響していることがわかります。
バルク層 (下グラフ): Si終端面（青線）のVBMは-1.23 eVにあり、SBHは1.23 eVと計算されています。C終端面（赤線）のVBMは-0.27 eVにあり、SBHは0.27 eVと計算されています。Al界面の場合と同様に、C終端面はオーミック特性に近いことがわかります。これに対し、Si終端面では明確なショットキーバリアが形成されており、実験値である1.4 eV とSi終端面の計算結果を比較すると、比較的良い一致を示していることがわかります。

まとめ#

本解析事例では、第一原理計算ソフトウェアAdvance/PHASEを用いて金属/4H-SiC界面のショットキーバリア高さ (SBH) を評価しました。層分割局所状態密度 (LayerDOS) の解析から、SBHが界面の終端面、金属の種類、金属層の厚さに依存することが明らかになりました。具体的には、全てのモデルでC終端面よりもSi終端面の方が大きなSBHを示し、金属をAlからCuに変えることでSBHに変化が見られました。さらに、Al/SiC界面において、金属層を1層から3層に増やすとオーミック的な接触からショットキー的な接触へと特性が変化し、SBHが増大しました。このように、第一原理計算は、実験だけでは観測が困難な原子レベルの現象を解明し、SBHの物理的起源の理解やデバイス設計のための重要な指針を与える強力なツールです。

参考文献#

S. M. Sze, Semiconductor Devices: Physics and Technology, John Wiley & Sons, 2008.
R. T. Tung, "The physics and chemistry of the Schottky barrier height", Appl. Phys. Rev. 1, 011304 (2014).
S. Tanaka, T. Tamura, K. Okazaki, S. Ishibashi, and M. Kohyama, "First-principles calculations of schottky barrier heights of monolayer metal/6H-SiC {0001} interfaces", Mater. Trans. 47, 2690 (2006).
C. G. Van de Walle and R. M. Martin, "Theoretical study of band offsets at semiconductor interfaces", Phys. Rev. B 35, 8154 (1987).
J. Kohlscheen et.al., "Band line-up determination at p- and n-type Al/4H-SiC Schottky interfaces using photoemission spectroscopy", J. Appl. Phys. 94, 3931 (2003).
T. Hatayama, K. Kawahito, H. Kijima, Y. Uraoka, and T. Fuyuki, "Electrical Properties and Interface Reaction of Annealed Cu/4H-SiC Schottky Rectifiers", Materials Science Forum 389, 925 (2002).