第一原理計算データを活用した中空粒子の光学設計・多層膜の光学特性解析#

Advance/PHASE Logo

酸化チタン(TiO₂)や酸化スカンジウム(Sc₂O₃)などの高屈折率材料は、その高い光散乱能や光閉じ込め効果を利用し、高隠蔽性塗料、化粧品、反射防止膜、光学フィルターなど幅広い分野で応用されています。近年、軽量化や光学特性の制御（白色度の向上など）を目的として、粒子内部を空洞化した「中空粒子（Hollow Particles）」の設計が注目されていますが、最適な光学特性を得るためには、材料の屈折率だけでなく、粒子径やシェル厚みといった幾何学的パラメータの精密な設計が不可欠です。本解析事例では、第一原理計算ソフトウェアAdvance/PHASEを用いて算出したSc₂O₃の精密な光学定数（複素屈折率）を入力値とし、中空粒子の形状最適化および多層膜ミラーの反射特性解析を実施することで、ミクロな物性値からマクロな製品性能を予測する一貫解析の有効性を実証しました。

Keywords: 第一原理計算（DFT）, 光学特性, 屈折率, 中空粒子, Mie散乱理論, 多層膜, 転送行列法, Sc2O3

解析手法と連携の指針#

1. 原子スケール：DFTによる光学定数の導出#

光学シミュレーションの精度は、入力となる材料物性値（屈折率 $n$ 、消衰係数 $k$ ）の正確さに依存します。既存の解析事例 [1] では、Sc₂O₃のバルク構造に対し、DFT（密度汎関数理論）計算を行い、誘電関数 $\varepsilon(\omega)$ を算出しました。実験値との乖離を補正するためにバンドギャップ補正（Scissor Operator）を適用し、可視光全域における高精度な複素屈折率データ $N(\lambda) = n(\lambda) - ik(\lambda)$ を取得しました。なお、複素屈折率の虚部符号は分野によって定義が異なりますが、本解析では一般的な光学・工学の慣習に従い、光の吸収を表す消衰係数 $k$ を正の値（ $k>0$ ）としており、Advance/PHASEで算出したk（正の値）と直接に対応しています。

2. スケール間連携：電磁光学シミュレーション#

DFT計算で得られた波長依存性を持つ複素屈折率を、以下のマクロ光学モデルへ連携させました。

※解析のポイント：微小な吸収の考慮

Sc₂O₃は可視光域でほぼ透明ですが、第一原理計算データに含まれる微小な虚部（消衰係数 $k$）を無視せず考慮することで、多層膜における吸収損失や、粒子による光減衰を厳密に評価しています。

(A) 中空粒子モデル (Mie Scattering Theory)#

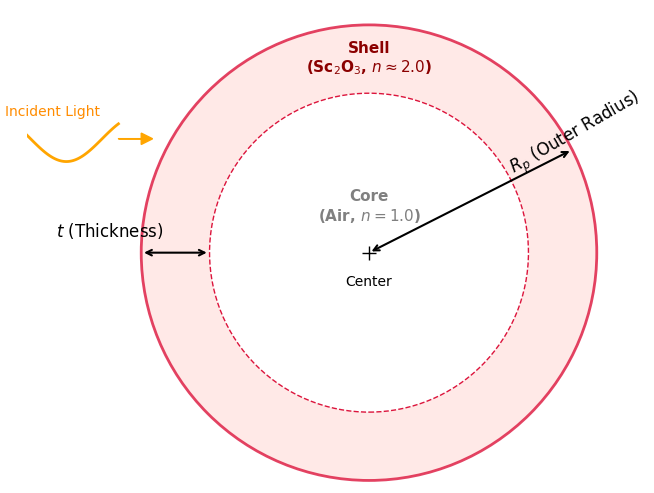
中空粒子の模式図

中空粒子を「空気コア(Core)＋Sc₂O₃シェル(Shell)」の2層球としてモデル化し、Aden-Kerker法（拡張Mie理論）[2] を用いて光学特性を算出しました。粒子単体の光学性能は、平面波が粒子によってどのように散乱・吸収されるかを示す、以下の「効率係数（Efficiency Factors, $Q$ ）」を用いて評価しました。

散乱効率 (Scattering): $Q_\text{sca} = \frac{2}{x^2} \sum_{n=1}^{\infty} (2n+1) (|a_n|^2 + |b_n|^2)$

消衰効率 (Extinction): $Q_\text{ext} = \frac{2}{x^2} \sum_{n=1}^{\infty} (2n+1) \text{Re}(a_n + b_n)$

吸収効率 (Absorption): $Q_\text{abs} = Q_{ext} - Q_{sca}$

後方散乱効率 (Backscattering): $Q_\text{back} = \frac{1}{x^2} \left| \sum_{n=1}^{\infty} (2n+1)(-1)^n (a_n - b_n) \right|^2$

ここで、 $a_n, b_n$ は粒子の屈折率分布から決定される散乱係数、 $x = 2\pi R_p / \lambda$ はサイズパラメータです（ $R_p$ : 粒子外半径、 $\lambda$ : 媒質中の波長）。
※なお、これらの効率係数 $Q$ は粒子の幾何学的断面積 $\pi R_p^2$ に対する比率として定義されるため、光の回折効果等により 1 (100%) を超える値を取り得ます（例: $Q_{sca} > 1$ は、粒子が自身の断面積よりも広い範囲の光を散乱していることを意味します）。

(B) 多層膜モデル (Transfer Matrix Method)#

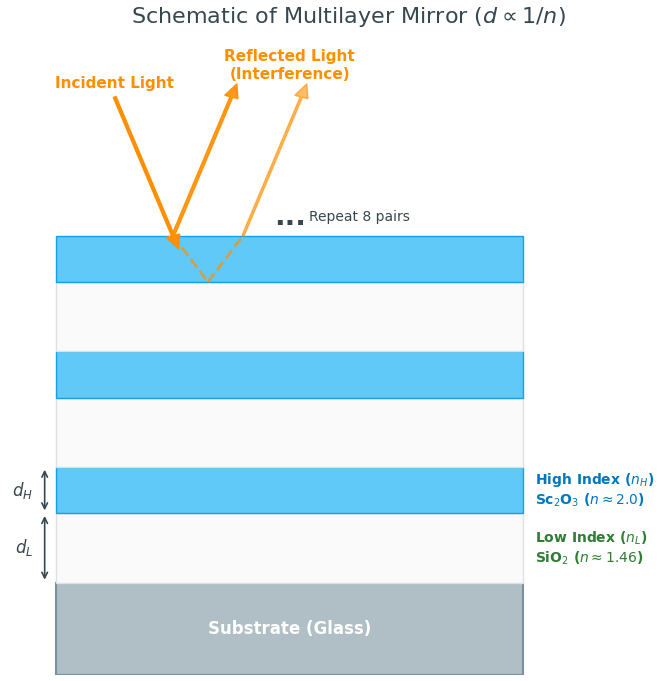
多層膜の模式図

Sc₂O₃（高屈折率層）とSiO₂（低屈折率層）を交互に積層した多層膜を対象とします。空気（ $n \approx 1.0$ ）からの入射光に対する反射率を最大化するため、最表面（入射側）には、空気との屈折率差が大きい「高屈折率材料（Sc₂O₃）」を配置しました。この多層膜に対して、転送行列法（Transfer Matrix Method）を用いて光学特性を算出しました。具体的には、第 $j$ 層の屈折率 $n_j$ 、膜厚 $d_j$ から定まる特性行列 $M_j$ を以下のように定義し、全層の行列積 $M$ を求めます。

$M = \prod_{j=1}^{N} M_j = \begin{pmatrix} m_{11} & m_{12} \\ m_{21} & m_{22} \end{pmatrix}$

得られた全行列 $M$ の要素を用いて、複素振幅反射率 $r$ および複素振幅透過率 $t$ を導出し、最終的にエネルギー反射率 $R = |r|^2$ 、透過率 $T = \frac{\text{Re}(n_s)}{\text{Re}(n_0)}|t|^2$ を算出しました。さらに、エネルギー保存則 $R + T + A = 1$ に基づき、吸収率 $A$ を決定しました。

計算条件#

Pythonスクリプトによる数値解析に用いた主なパラメータを表1に示します。

表1. 光学シミュレーションの入力パラメーター

カテゴリー	パラメーター	設定値
材料物性	高屈折率材料	Sc₂O₃ (補正済みDFTデータ)
	低屈折率材料/媒質	SiO₂ (n=～1.46、波長依存性あり) [3] / 空気 (n=1.0)
中空粒子モデル	粒子外径 ( $D = 2R_p$ )	400 nm
	シェル厚み ( $t$ )	10 nm ～ 200 nm (変数)
	コア材料	空気 (n=1.0)
多層膜モデル	設計中心波長	550 nm (緑色光)
	層構成	(Sc₂O₃/SiO₂) × 8ペア
	高屈折率層厚 ( $d_H$ )	約 70.3 nm ( $\lambda / 4n_H$ )
	低屈折率層厚 ( $d_L$ )	約 94.2 nm ( $\lambda / 4n_L$ )

解析結果と考察#

1. 中空粒子の形状最適化#

図1に、粒子外径を400nmに固定し、Sc₂O₃のシェル厚みを変化させた場合の散乱特性を示します。

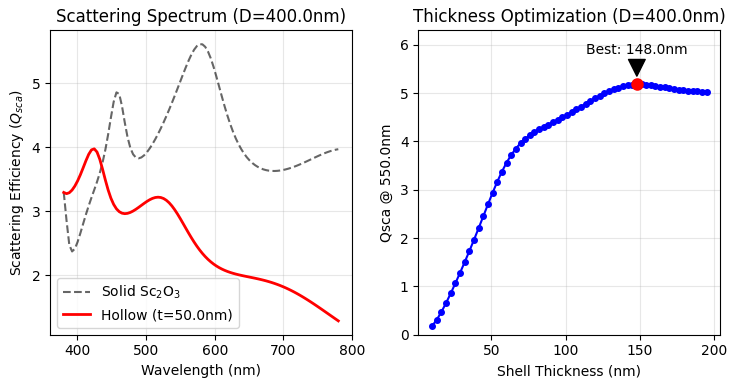
中空粒子の散乱スペクトルと厚み依存性
図1. (左) 散乱効率スペクトルの比較、(右) 波長550nmにおけるシェル厚みと散乱効率の関係

スペクトル比較と物理メカニズム：
図1左に示すように、中実粒子（Solid, 点線）と比較して、中空粒子（Hollow, 赤線）は波長によって散乱効率が複雑に振動します。これは、酸化チタン中空粒子を用いた色素増感太陽電池の研究 [4] などでも光閉じ込め効果（Light Trapping）の要因として報告されている、内部空洞での多重反射（multiple-reflection）およびそれに伴う光の干渉効果に起因すると考えられます。

シェル厚みの最適化結果：
図1(右)の通り、シェル厚みを変化させた結果、約148 nm 付近に散乱効率の極大値が確認されました。しかしながら、図1(左)の比較からも分かるように、本解析の粒子サイズ（D=400nm）においては、シェルを薄くして中空化を進めるよりも、中実（Solid）に近い厚いシェル構造の方が550nm付近の散乱効率が高くなることが明らかになりました。

このことから、本条件下では「中空化による多重反射・干渉効果」よりも、「高屈折率材料の体積減少による散乱能低下」の影響が支配的であると考えられます。

また、図2に各光学効率（散乱 $Q_\text{sca}$ 、吸収 $Q_\text{abs}$ 、後方散乱 $Q_\text{back}$ ）の波長依存性を示します。 $Q_\text{abs}$ （赤線）が全域でほぼゼロであることから、DFT計算で得られたSc₂O₃が高い透明性を持ち、光エネルギーを熱ロスすることなく効率的に散乱させていることが確認できました。

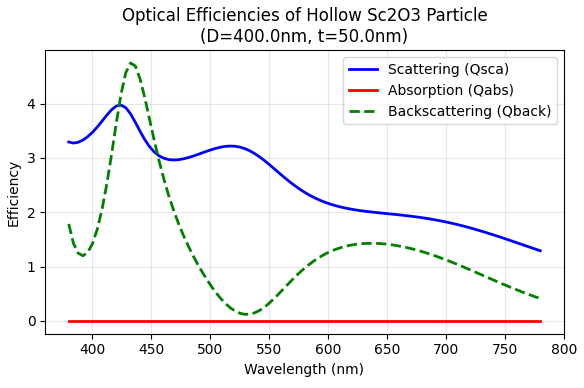
中空粒子の光学効率
図2. 中空Sc₂O₃粒子の光学効率係数 (D=400nm, t=50nm)

2. 多層膜ミラーの光学特性#

次に、DFTデータに基づき設計したブラッグ反射ミラー（中心波長550nm）の特性評価結果を図3に示します。ここでは低屈折率層として、Fused Silicaの分散式（Malitson, 1965）[3] を用いて算出されたSiO₂の屈折率を適用しました。

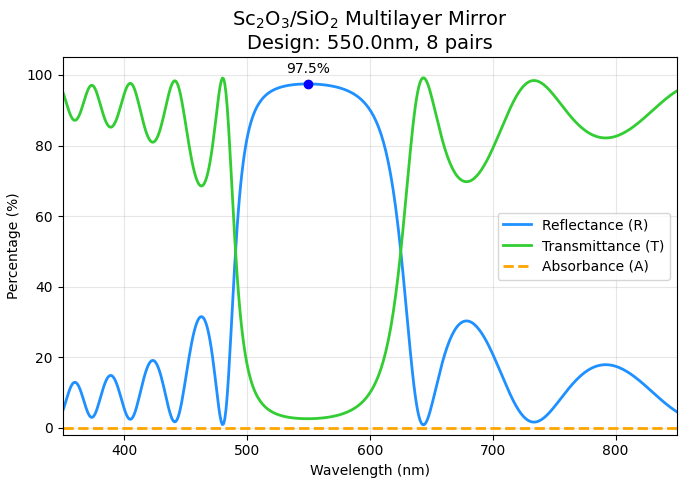
多層膜の反射率・透過率・吸収率
図3. Sc₂O₃/SiO₂ 8ペア多層膜の光学特性 (R/T/A)

550nmを中心に、反射率（青線）がほぼ100%に達するフォトニックバンドギャップが明瞭に形成されています。また、吸収率（オレンジ点線）も算出されており、材料固有の微小な吸収や、多重反射による光閉じ込め効果の影響を定量的に評価できています。なお、本解析で使用したSc₂O₃の屈折率分散データは、文献値 [5] と比較しても可視光域で良好な一致を示しており、第一原理計算による光学定数算出の精度の高さが、最終的なデバイス性能予測の信頼性を裏付けています。

まとめ#

本解析では、第一原理計算ソフトウェアAdvance/PHASEを用いたDFT計算とマクロな電磁光学理論（Mie理論、転送行列法）を連携させ、Sc₂O₃を用いた光学材料の特性評価を行いました。多層膜ミラーの解析においては、正確な屈折率と物理法則に基づいた層厚設計（ $d = \lambda / 4n$ ）を行うことで、可視光域で高い反射率が得られる理論的な可能性が示されました。また、中空粒子の形状検討においては、対象とした粒子径（400nm）の条件下では、中空化による散乱効率の向上効果は限定的であり、中実に近い構造が有利となる傾向が示唆されました。ただし、本解析は単分散・真球を仮定した理想的なモデルに基づく理論限界値です。実際の製品開発においては、粒度分布の広がりやバインダー中での分散状態、界面ラフネスなどが光学特性に影響を与えるため、これらの因子をあらわに考慮してより詳細なモデル化が必要な場合があります。本手法は、実験前の一次スクリーニングや、材料設計の初期指針を得るための有効なツールとして活用が期待されます。

本解析の詳細や、光学材料設計への適用に関するご相談はこちら

お問い合わせ

参考文献#

第一原理計算による金属酸化物の屈折率解析
C. F. Bohren and D. R. Huffman, "Absorption and Scattering of Light by Small Particles", Wiley-VCH, 1998.
I. H. Malitson, "Interspecimen Comparison of the Refractive Index of Fused Silica", J. Opt. Soc. Am. 55, 1205 (1965).
C. Dwivedi, V. Dutta, A. K. Chandiran, M. K. Nazeeruddin, and M. Grätzel, "Anatase TiO₂ Hollow Microspheres Fabricated by Continuous Spray Pyrolysis as a Scattering Layer in Dye-Sensitised Solar Cells", Energy Procedia 33, 223 (2013).
M. N. Polyanskiy, "Refractiveindex.info database of optical constants", Sci. Data 11, 94 (2024).