コンテンツにスキップ

第一原理計算による金属酸化物の屈折率解析#

PHASE logo

レンズや光学薄膜、光ファイバーといった光学材料の設計において、屈折率は最も基本的な物性値の一つです。特に、2.0を超えるような高い屈折率を持つ「高屈折率材料」は、スマートフォンのカメラレンズの薄型化や、高性能な反射防止膜の設計に不可欠な存在となっています。金属酸化物である酸化チタン(TiO2)や酸化ジルコニウム(ZrO2)などは、こうした高屈折率材料の代表例です。第一原理計算は、このような重要な材料の光学特性を実験前に予測できる強力なツールとなります。本事例では、第一原理計算ソフトウェアAdvance/PHASEを用い、これらの金属酸化物を対象として、バンドギャップ補正が屈折率の予測精度に与える効果を実証します。

Keywords: 第一原理計算, 屈折率, 高屈折率材料, バンドギャップ補正, ハサミ打ち法, 密度汎関数理論(DFT), 金属酸化物

計算理論：屈折率計算とバンドギャップ補正#

第一原理計算では、屈折率を直接計算するのではなく、光の周波数の関数である複素誘電関数 を介して算出します [1]。

  1. 誘電関数の虚部()の計算: DFT計算で得られた電子バンド構造に基づき、価電子帯から伝導帯への光吸収（電子遷移）の確率を計算します。これがに対応します。
  2. 誘電関数の実部()の計算: から数学的な積分変換であるクラマース・クローニッヒの関係式を用いてを導出します。
  3. 屈折率()の導出: 最終的に、以下の式を用いて屈折率を求めます。

ここで重要となるのが、計算の出発点であるバンド構造の正確さです。本解析で使用した汎関数GGA-PBEなどの標準的な手法は、バンドギャップ()を実験値より30～50%小さく評価する傾向があります。バンドギャップが過小評価されると、の吸収スペクトルの開始点が低エネルギー側にずれ、結果として、ひいては屈折率が過大に評価されてしまいます。

この問題を解決する最も簡便かつ効果的な手法がハサミ打ち法（Scissor Operator）です [2]。これは、計算で得られたバンドギャップと実験値との差分だけ、伝導帯のエネルギー準位を引き上げる（ハサミで切り開くようにシフトさせる）補正方法です。この単純な操作により、のスペクトルが正しい位置に補正され、屈折率の計算精度が大幅に向上します。

計算モデル#

本解析では、光学材料として重要な金属酸化物の中から、結晶構造の異なるAO2型（図1）とA2O3型（図2）の計5種類のモデルを対象としました。

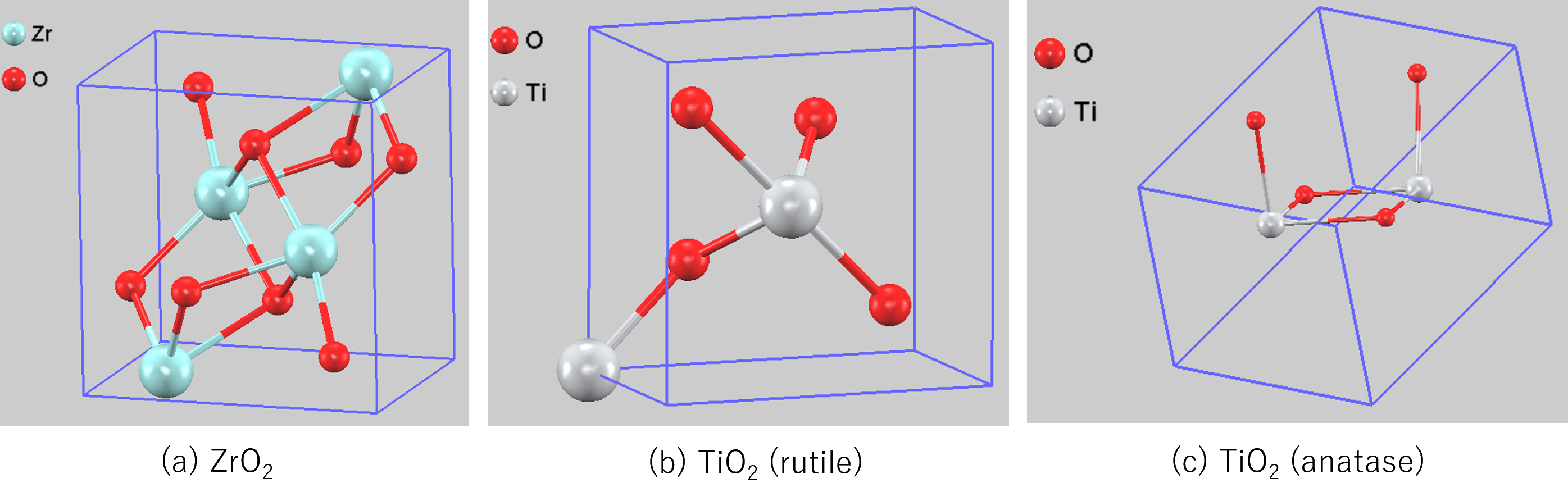
AO2の結晶構造
図1.　AO2の結晶構造: (a) バッデレ石型ZrO2 (b) ルチル型TiO2 (c) アナターゼ型TiO2

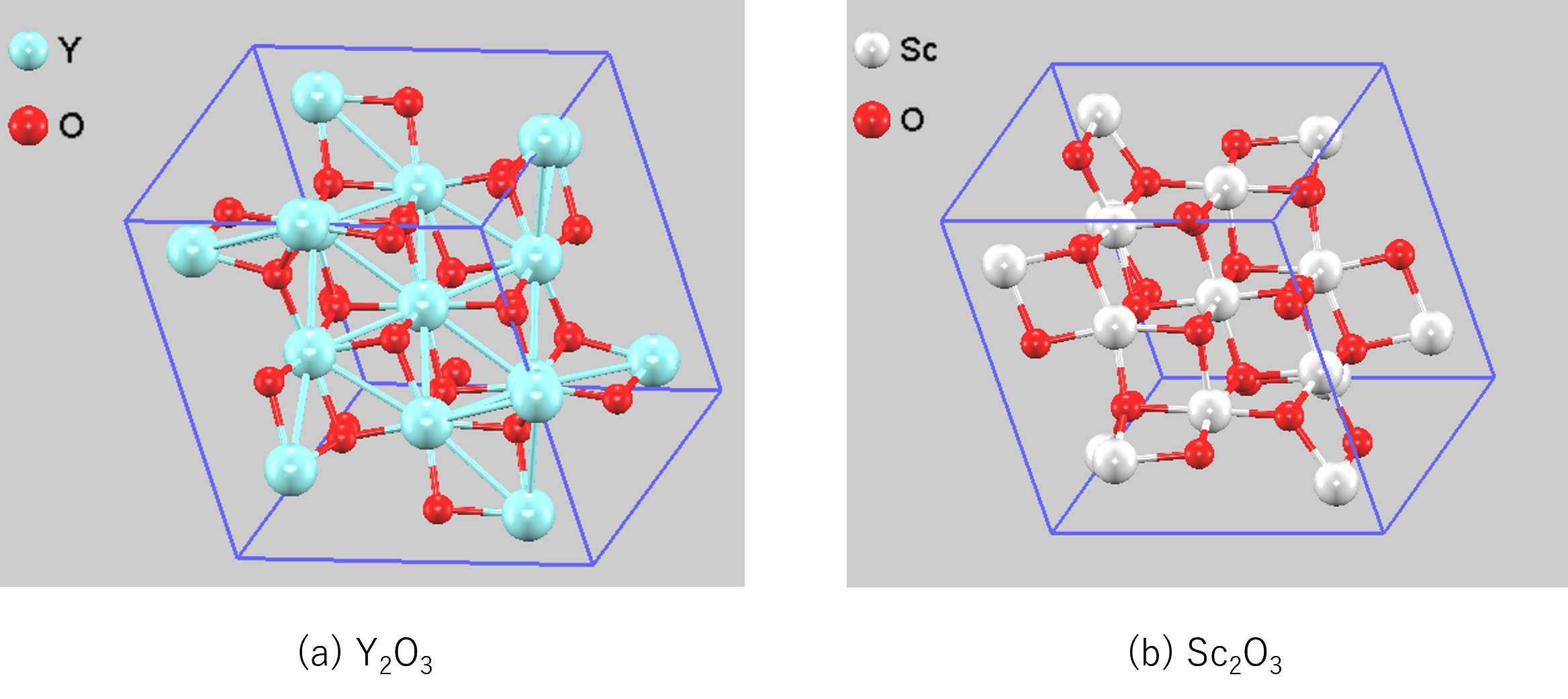
A2O3の結晶構造
図2.　A2O3の結晶構造: (a) ビクスバイト型Y2O3 (b) ビクスバイト型Sc2O3

計算結果と考察#

表1に、各酸化物についてバンドギャップ補正の有無による屈折率（）の計算値と実験値 [3, 4] を比較して示します。ここで、とは、光源としてナトリウムのD線（波長: 589.3 nm、エネルギー: 2.11 eV）を用いたときの屈折率を指します。

表1. 各種金属酸化物の屈折率()の計算値と実験値（補正はバンドギャップ補正です）

補正値 (eV) 屈折率
(計算値, 補正なし)		 屈折率
(計算値, 補正あり)		 屈折率
(実験値)
ZrO2 2.27 2.36 2.09 2.16
TiO2 (rutile) 1.11 2.96 2.52 2.61
TiO2 (anatase) 1.06 2.92 2.46 2.55
Y2O3 1.57 1.97 1.82 1.87
Sc2O3 2.14 2.16 1.95 1.99

まず、表1の全体的な傾向から議論します。

  • GGA計算の系統的誤差: 全ての材料において、「補正なし」の計算値は実験値を系統的に上回る結果となりました。これは理論のセクションで述べた通り、GGA汎関数がバンドギャップを過小評価することに起因する典型的な傾向です。
  • ハサミ打ち補正の有効性: 一方で、「補正あり」の計算値は、全てのケースで実験値に近づくように改善されています。特にTiO2やY2O3では、補正後の値が実験値と非常に近くなっており、この簡便な補正手法が多くの材料に対して有効であることが示唆されます。

次に、この傾向をより詳しく理解するため、代表例としてSc2O3の屈折率分散（波長依存性）をグラフ化したものを図3に示します。

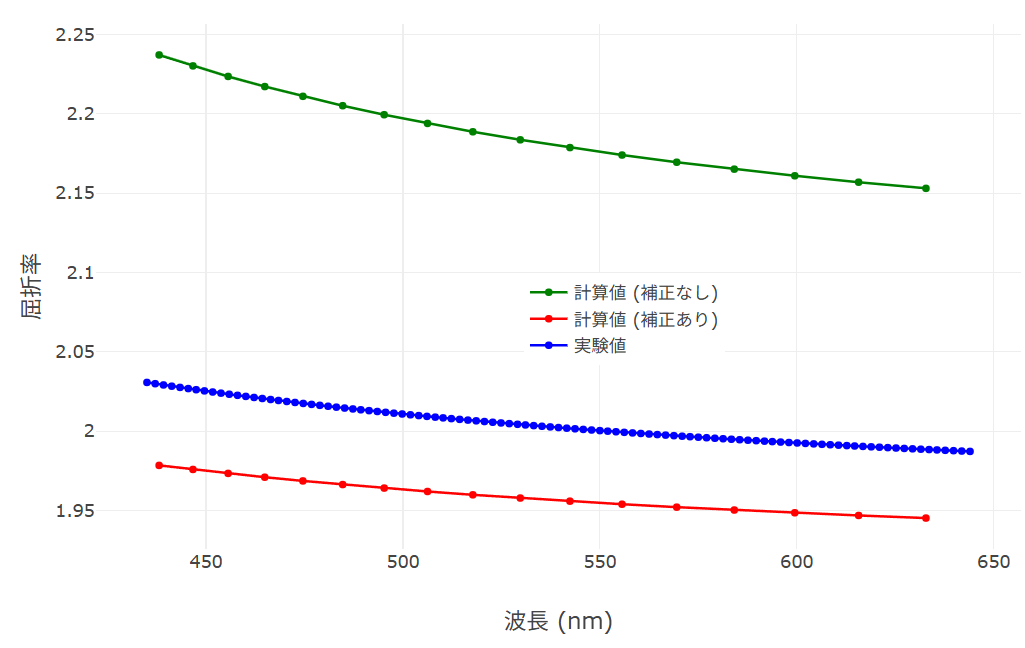
Sc2O3の屈折率分散グラフ
図3.　Sc2O3の屈折率分散の比較。実験値は文献 [3] より引用。

図3から明らかなように、緑線で示す「補正なし」の値は、可視光域の全域にわたって実験値（青線）から大きく乖離しています。一方で赤線の「補正あり」の値は、実験値のカーブとほぼ平行な軌跡を描いており、分散の傾向（波長が短くなるにつれて屈折率が大きくなる度合い）を良く再現できていることが確認できます。

このように、第一原理計算におけるハサミ打ち補正は、単一波長（D線）での屈折率の絶対値を改善するだけでなく、より広い波長域における材料の光学的挙動を定性・準定量的に予測する上でも有効な手法であると言えます。ただし、ハサミ打ち補正をしても改善しない系もあることが知られており、その原因究明と、より汎用的な補正手法の開発が今後の課題として挙げられます。

まとめ#

本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、5種類の金属酸化物の屈折率計算におけるバンドギャップ補正の重要性を示しました。標準的なGGA計算は屈折率を系統的に過大評価しますが、実験値に合わせてバンドギャップを補正するハサミ打ち法を適用するだけで、計算精度が大幅に向上し、これらの材料で実験値をよく再現できることが確認されました。計算コストの低いハサミ打ち補正は、より高精度な第一原理計算手法（例：GW近似など）を適用する前に、例えば材料スクリーニングや設計初期段階において有効なアプローチと言えるでしょう。

参考文献#

  1. M. Fox, Optical Properties of Solids, 2nd Edition, Oxford University Press, 2010.
  2. Z. H. Levine and D. C. Allan, "Linear optical response in silicon and germanium including self-energy effects", Phys. Rev. Lett. 63, 1719 (1989).
  3. M. N. Polyanskiy, "Refractiveindex.info database of optical constants", Sci. Data 11, 94 (2024). Database URL: https://refractiveindex.info
  4. E. D. Palik (Ed.), Handbook of optical constants of solids (Vol. 3), Academic press, 1998.

関連ページ#