Phase Field法との連携によるCu-Au合金の組織形成過程の解析#

PHASE logo

材料の機械的特性や磁気特性は、その微細組織（マイクロストラクチャ）に大きく依存します。金属間化合物の析出や規則相の形成プロセスを計算機上で再現・評価することは、材料設計において極めて重要です。本事例では、第一原理計算ソフトウェアAdvance/PHASEを用いて密度汎関数法 (DFT)でCu-Au合金の生成エンタルピーを算出し、それをPhase Fieldモデルの入力パラメータ決定の指針（参照値）として用いるマルチスケール解析の基礎検討を行いました。さらに、マルチバリアント弾性場モデルへと拡張することで、Cu-Au特有の双晶界面（Twin boundary）形成のメカニズムや、バリアント間の競合プロセスを定性的に再現可能であることを示しました。

Keywords: 第一原理計算, DFTシミュレーション, Phase Field法, マルチスケール解析, Cu-Au, 規則化, 組織形成 (microstructure formation), 弾性場, 微視的弾性理論

1. 基礎検討：熱力学的駆動力のみによる解析#

解析の背景とモデル#

Phase Field法 [1] は、界面（相と相の境界）を数学的に連続な場として扱う計算手法です。従来の界面追跡法とは異なり、複雑な界面形状の変化や、相の分離・合体、結晶粒の成長などを自然に再現できるのが特徴です。本事例では、Cu-Au合金における「不規則相（Disordered phase）」から「規則相（Ordered L1₀）」への変態を扱います。このプロセスは、保存されない秩序変数 $\phi$ の時間発展を記述するAllen-Cahn（アレン・カーン）方程式によってモデル化されます [1]。

$\frac{\partial \phi}{\partial t} = -M \left( \frac{\partial f_{local}}{\partial \phi} - \epsilon^2 \nabla^2 \phi \right)$

ここで、 $\phi$ は秩序変数（ $\phi=0$ : 不規則相、 $\phi=\pm 1$ : 規則相の異なる反位相ドメイン）、 $M$ は界面移動度、 $\epsilon$ は界面エネルギーに関連する係数です。項 $f_{local}$ は局所自由エネルギー密度であり、本検討ではダブルウェルポテンシャル（二重井戸型）を用います。

$f_{local}(\phi) = W (\phi^2 - 1)^2$

この二重井戸型ポテンシャルにおいて、係数 $W$ は不規則状態（ $\phi=0$ ）と安定な規則状態（ $\phi=\pm 1$ ）との間のエネルギー差に対応します。本解析では、第一原理計算で得られた生成エンタルピー $\Delta H$ の絶対値を基準とし、Phase Field法における数値計算上のスケーリングを施して $W$ を決定しました。これにより、純粋に現象論的なパラメータフィッティングではなく、第一原理計算に基づく熱力学的傾向を考慮した駆動力を設定して計算を行っています。

計算手順#

解析は以下の2ステップで実施しました。

第一原理計算 (DFT):
Advance/PHASEを用い、CuAu (L1₀構造) の生成エンタルピー $\Delta H$ を計算しました [2]。
Phase Fieldシミュレーション (Python):
DFTで得られた生成エンタルピー $\Delta H$ を、不規則相と規則相の間の熱力学的な駆動力（エネルギー差）のスケール基準として採用しました。これにより、現象論的なパラメータフィッティングのみに頼るのではなく、第一原理計算に基づく物理的傾向を反映させたPhase Fieldシミュレーションを行いました。

表1. 計算条件とパラメータ

項目	設定値 / 出所
DFT: 生成エンタルピー ( $\Delta H$ )	-0.0710 eV/atom (Advance/PHASE計算値 [2]) ※ポテンシャル深さ $W$ の基準値として参照
界面パラメータ ( $\epsilon$ )	2.0 (計算グリッドに対し界面幅を確保するためのモデル値)
移動度 ( $M$ )	1.0 (基準化された無次元値)
支配方程式	Allen-Cahn方程式（2次元、単一バリアントモデル）
計算グリッド	120 $\times$ 120

注記：モデルの簡易化およびパラメータ設定について
本シミュレーションは定性的な基礎検討であり、定量的な予測（温度・時間）を目的としたものではありません。以下の設定および簡易化を行っています。

(1) ポテンシャル障壁高さ $W$ のスケーリング：
DFT計算値 $\Delta H$ をそのまま用いると界面幅が極端に狭くなり、Phase Field法（連続体モデル）での記述が困難になります。そのため、正規化係数 $C_\text{norm}$ を導入し、計算グリッド幅 $dx$ に対して界面が適切な幅（約4～5 $dx$）を持つように $W$ をスケーリングしています。これにより、数値計算上の安定性と物理的なドメイン形状の表現を両立させています。
(2) 単位系：本計算は無次元化された単位系で行っています。現実の時間・長さスケールへの換算には、界面エネルギーや移動度の実測値等を用いた別途スケーリングが必要です。
(3) 秩序変数の簡易化：本来のCuAu (L1₀) 変態は複数のバリアントを持つ複雑な現象ですが、本検討では現象を単純化し、単一バリアント内での反位相境界（APB）形成のみを表現するスカラー変数モデルを用いています。
(4) 相転移の次数に関する近似：
本来、Cu-Auの規則化は核生成・成長を伴う一次相転移ですが、本基礎検討では現象の理解を容易にするため、スピノーダル分解と同様の連続的な不安定性（二次相転移的挙動）として近似しています。より厳密な一次相転移の記述については、後述の「2. 発展検討」にて高次項を含むLandauポテンシャルを用いて扱っています。

シミュレーション結果と考察#

図1に、Phase Fieldシミュレーションによって得られたCuAu合金の組織形成プロセスを示します。

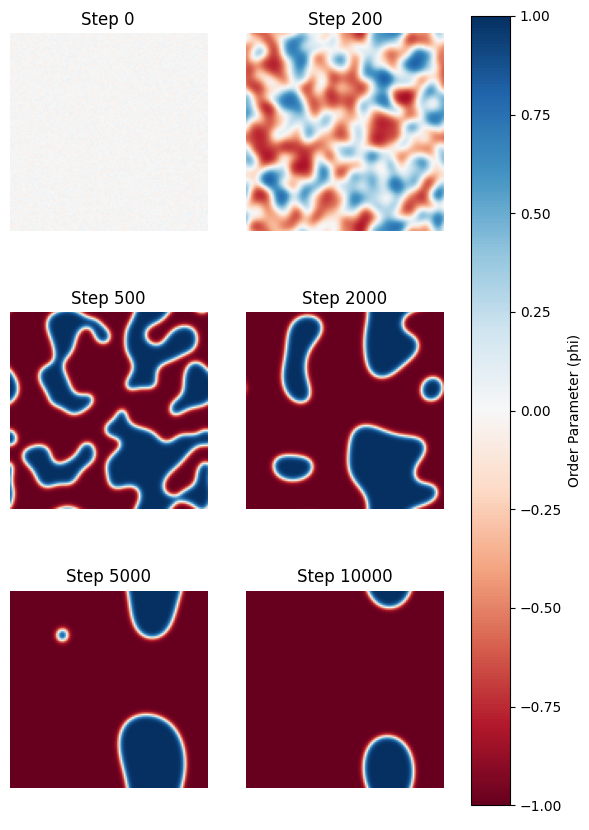
Microstructure Evolution of CuAu
図1. 第一原理計算のエネルギー値を入力したCuAu合金の組織形成シミュレーション（2次元）。
青色 ( $\phi=+1$ ) と赤色 ( $\phi=-1$ ) は、同一配向バリアント内における原子配列の位相（stacking phase）が異なる2つの規則相ドメインを表しており、白色 ( $\phi \approx 0$ ) は不規則相に対応します。

組織形成のプロセス#

Step 0 → 200 (秩序化不安定性によるドメイン形成):
不規則状態（ $\phi \approx 0$ ）の初期微動から、急速に明瞭なドメイン構造（ $\phi \approx \pm 1$ ）が形成されています。系が不安定領域にあるため、スピノーダル分解と同様の「秩序化不安定性（Ordering Instability）」により、核生成障壁なしに相変態が進行しています。
Step 500 → 2000 (反位相境界の形成):
異なる位相を持つ規則相ドメイン（青：ドメインA、赤：ドメインB）が衝突し、有限の幅を持つ「反位相境界（Anti-Phase Boundary: APB）」が形成され、迷路状の組織が確認できます。
Step 5000 → 10000 (曲率駆動による領域粗大化):
微細なドメインが消滅し、界面が滑らかになりながら全体のドメインサイズが増大しています。系全体の界面自由エネルギーを最小化しようとする熱力学的な駆動力により、粗大化（Coarsening）が進行しています。

2. 発展検討：マルチバリアントと弾性場による組織制御#

現実のCu-Au合金では、L1₀構造への変態に伴い結晶格子が正方晶歪み（c軸方向への縮み）を起こします。結晶の対称性から、c軸の向きが異なる3つの「バリアント（x軸, y軸, z軸配向）」が存在し、これらが競合することで複雑な組織が形成されます。

そこで、モデルを以下の通り拡張し、より現実的な組織形成シミュレーションを行いました [1]。

マルチバリアント化: 3つの秩序変数 $\eta_1, \eta_2, \eta_3$ を導入し、結晶方位の異なるドメインの競合を記述。
弾性場の導入: Khachaturyanの微視的弾性理論に基づき、バリアント間の格子不整合による長距離弾性相互作用を計算。

Landau 2-4-6 多項式ポテンシャル#

単純な二重井戸型ではなく、高次の項を含む展開を行うことで、不規則相（ $\eta=0$ ）と規則相（ $\eta \neq 0$ ）の間のエネルギー障壁を物理的に表現し、一次相転移挙動を記述しました。

$f(\eta) = \frac{A(T)}{2}\eta^2 - \frac{B}{4}\eta^4 + \frac{C}{6}\eta^6$

$\frac{\partial \eta_p}{\partial t} = -M \left( \frac{\delta F_\text{chem}}{\delta \eta_p} + \frac{\delta E_\text{el}}{\delta \eta_p} \right), \quad (p=1,2,3)$

ここで、各項は以下の物理的意味を持ちます：

$A(T), B, C$ : ポテンシャルの形状を決める係数。 $A(T)$ に温度依存性を与えることで、任意の温度における過冷却度を表現し、熱処理プロセス（冷却速度など）の違いによる組織変化を模擬することが可能です。
$\eta_p$ : $p$ 番目のバリアント（配向）の規則度を表す秩序変数。
$F_\text{chem}$ （化学的駆動力）: 物質が混ざり合ったり規則化したりしようとする化学的なエネルギー。
$E_\text{el}$ （弾性的駆動力）: 格子の歪みを解消しようとする弾性エネルギー。この2つの力のバランスで組織が進化します。

弾性場（Khachaturyanの微視的理論）#

バリアント間の格子不整合による長距離弾性相互作用を、Green関数法を用いて厳密に計算しました。

$E_\text{el} = \frac{1}{2} \int \frac{d^3k}{(2\pi)^3} B_{pq}(\mathbf{k}) \tilde{\theta}_p(\mathbf{k}) \tilde{\theta}_q^*(\mathbf{k})$

※ この式はフーリエ空間（波数 $\mathbf{k}$ 空間）での積分を表しています。実空間での計算では負荷が極めて高い「長距離弾性相互作用」を、周波数領域に変換することで高速かつ厳密に評価しています。 $B_{pq}(\mathbf{k})$ は物質の弾性定数と結晶方位から決定される係数行列です。

モデルの改善点：界面の先鋭化処理 (Interface Sharpening)
数値計算上の界面幅（Diffuse Interface）を確保しつつ、物理的なドメイン形状（ファセット）を損なわないよう、弾性エネルギー項への重み付け調整を行い、鋭い界面形状を復元しました。

使用した文献パラメータ#

第一原理計算の結果に加え、表2の実験・文献値 [3, 4]をシミュレーションに組み込みました。

本解析では、組織形成の幾何学的特徴を決定づける「固有歪み（Eigenstrain）」の算出において、第一原理計算と実験データの連携を行いました。具体的には、変態前の不規則相（FCC）については一般的な文献値を基準とし、変態後の規則相（L1₀）についてはAdvance/PHASEを用いた第一原理計算により平衡格子定数を決定しました [2]。なお、算出された規則相の格子定数は文献値と非常に良い一致を示しており、第一原理計算の予測精度の高さが確認されました。この検証を経たDFT計算値と、基準となる不規則相の格子整合性から固有歪みを定義し、マルチバリアント弾性場モデルへ導入しています。

また、弾性定数については、純Cuおよび純Auの文献値を用いた線形近似（Rule of Mixtures）により設定し、バリアント間の弾性相互作用を考慮しました。

本解析では、計算コストと現象理解の効率性を重視し、2次元平面歪み状態での解析を行いました。Cu-Au合金における双晶形成やAPBの挙動といった主要な微視的メカニズムは、2次元モデルでも十分に定性的な再現が可能であり、自己組織化プロセスの支配因子を特定する上では有効なアプローチです。

表2. 発展検討における入力パラメータ（文献・DFT値参照）

項目	設定内容
弾性定数 $C_{ij}$	$C_{11}=180, C_{12}=142, C_{44}=59$ GPa （強い弾性異方性を考慮）
固有歪み (Eigenstrain)	a軸: +2.8%, c軸: -4.6% （正方晶変態に伴う体積変化と変形）
境界条件	平面歪み状態 (Plane Strain) ( $\epsilon_{zz} = 0$ を仮定、2次元断面解析)

※ 本事例は解析フローの構築を主眼としているため、不規則相の弾性定数には純金属の混合則（Rule of Mixtures）を用いた一次近似を採用しました。なお、より厳密な定数決定が必要な場合は、SQS（Special Quasirandom Structures）法を用いたDFT計算により、固溶体状態の物性を評価するアプローチも可能です。

シミュレーション結果（マルチバリアントモデル）#

図2に、3つのバリアントと弾性相互作用を考慮した組織成長プロセスを示します。

Multi-variant Simulation Result
図2. マルチバリアントPhase Field法によるCuAu合金の組織形成（改良モデル）。
色（スチールブルー・オレンジ・セージグリーン）はそれぞれ異なる結晶方位（x, y, z軸）を持つ規則相バリアントを表し、白色は不規則相またはドメイン境界に対応します。弾性相互作用の寄与を適切に考慮することで、微細な双晶組織が安定化しています。

考察：双晶組織の自己組織化と安定化#

Step 0 → 1250 (秩序化の開始と相分離):
白色の不規則相の中から、秩序化不安定性（Ordering instability）により規則相ドメインが浮かび上がっています。Landauポテンシャルの効果により、スピノーダル分解的な相分離が初期段階として進行し、淡い青（Variant X）やオレンジ（Variant Y）の領域が形成され始めています。
Step 1500 → 2000 (ドメインの明瞭化と競合):
ドメインの輪郭が急速に明確になります。熱力学的駆動力のみを考慮した基礎検討（第1節）ではドメインの粗大化が進行しましたが、本モデルでは強い弾性相互作用が働くため、単一の巨大なドメインになるのではなく、互いの格子歪みをキャンセルし合う配置（青とオレンジの隣接）が優先的に選択されています。
Step 4000 (双晶界面の形成):
青（X軸配向）とオレンジ（Y軸配向）のバリアントが接する境界において、明瞭な45度の直線的な界面（Twin Boundary）が形成されました。これは弾性エネルギーを最小化する $\{110\}$ 面に対応しており、典型的な双晶組織の特徴を示しています。
Step 8000 (ラメラ組織の安定維持):
特筆すべき点として、長時間経過後も粗大化（単一バリアント化）せず、周期的なラメラ状の双晶組織が維持されています。これは、界面エネルギーによる「界面を減らそうとする力」に対し、弾性エネルギーによる「歪みを緩和するために層状に並ぼうとする力」が拮抗・優勢となったことを示しており、実際のCu-Au合金で見られる微細組織の特徴 [5] をより正確に再現できています。

なお、本計算結果においてセージグリーン（Z軸配向バリアント）が限定的であるのは、平面歪み（Plane Strain）条件下ではZ軸方向への変形が拘束され、面内（X, Y方向）で歪みを緩和できるバリアントの組み合わせがエネルギー的に有利となるためです。

第一原理計算とPhase Field法連携の意義#

本事例のように第一原理計算結果（生成エンタルピー等）を入力パラメータの基準として用いることで、実験データが乏しい材料系に対しても、熱力学的な傾向を反映した組織形成シミュレーションが可能となります。これは、原子スケールの知見をメゾスケールの組織予測へ橋渡しする第一歩として有用なアプローチです。また、本事例ではPythonによるプロトタイプ計算を行いましたが、より複雑な実用材料への適用には、大規模並列計算フレームワークの活用が推奨されます。例えば、MOOSE (Multiphysics Object Oriented Simulation Environment) [6] や FiPy [7] などのオープンソースツールは、Phase Field方程式のような非線形偏微分方程式を効率的に解くための高度なソルバーを備えています。これらのツールと第一原理計算・熱力学データベースを連携させることで、3次元的な複雑形状、多結晶組織、あるいは温度場・応力場が連成した現実的な製造プロセスのデジタルツイン構築へと展開することが期待されます。

まとめ#

Advance/PHASEによる第一原理計算と、PythonによるPhase Field法シミュレーションを連携させ、Cu-Au合金の組織形成過程を解析しました。単一バリアントモデルでは熱力学的な相分離傾向のみが示されましたが、マルチバリアント弾性場モデルへと拡張することで、Cu-Au特有の双晶界面の形成やバリアント間の競合、および弾性相互作用による微細組織の安定化プロセスを再現し、その形成メカニズムを可視化できることを示しました。この定性的なモデルをさらに定量的な解析（温度・時間）へと拡張するには、界面エネルギーや移動度について、DFT計算値や実測値に基づくパラメータ調整、および3次元計算の導入が必要となります。

本解析の詳細や、研究への適用可能性に関するご相談はこちら

お問い合わせ

参考文献#

L.-Q. Chen, "Phase-Field Models for Microstructure Evolution", Annu. Rev. Mater. Res. 32, 113 (2002).
Cu-Au二元系金属間化合物のConvex Hullと熱力学的安定性の第一原理計算
G. Simmons and H. Wang, Single crystal elastic constants and calculated aggregate properties: A Handbook, 2nd ed., MIT Press, Cambridge, MA (1971).
P. Villars, Pearson's Handbook: Crystallographic Data for Intermetallic Phases, ASM International, Amsterdam (1997).
M. Hirabayashi and S. Weissmann, "Study of CuAu I by transmission electron microscopy", Acta Metall. 10, 25 (1962).
D. Gaston, C. Newman, G. Hansen, and D. Lebrun-Grandie, "MOOSE: A parallel computational framework for coupled systems of nonlinear equations", Nucl. Eng. Des. 239, 1768 (2009).
J. E. Guyer, D. Wheeler, and J. A. Warren, "FiPy: Partial differential equations with Python", Comput. Sci. Eng. 11, 6 (2009).