結晶粒界の第一原理シミュレーション：Al Σ3 (111)ねじり粒界のエネルギー評価#

PHASE logo

多くの工業材料は、微小な結晶粒が集まって構成される多結晶材料です。これらの結晶粒の境界は「結晶粒界」と呼ばれ、材料の強度、破壊靭性、腐食耐性といった機械的特性に極めて大きな影響を与えます。粒界の構造とエネルギーを正確に理解することは、高性能な材料を設計する上で不可欠です。本解析では、第一原理計算ソフトウェアAdvance/PHASE を用い、アルミニウム(Al)の代表的な粒界である「Σ3 (111)ねじり粒界」のエネルギーを計算します。これはエネルギーが極めて低い安定な整合境界（コヒーレントな双晶境界）として知られており、理論計算のベンチマークとしても頻繁に用いられるため、計算の妥当性を検証する上で最適な対象です。

Keywords: 第一原理計算, 結晶粒界, 粒界エネルギー, Work of separation, アルミニウム

計算方法：結晶粒界エネルギーの算出#

結晶粒界エネルギー( $\gamma_\text{GB}$ )は、粒界を含むモデルの全エネルギーから、同じ原子数の完全な結晶（バルク）のエネルギーを差し引き、粒界面積で規格化することで算出されます。

$\gamma_\text{GB} = \dfrac{E_\text{GB} - n_\text{GB}E_\text{bulk}}{2A_\text{GB}}$

$\gamma_\text{GB}$ : 粒界エネルギー (J/m²)
$E_\text{GB}$ : 粒界を含む構造モデルの全エネルギー
$n_\text{GB}$ : 粒界モデルに含まれる原子の数
$E_\text{bulk}$ : バルク（欠陥のない完全な結晶）における原子1個あたりのエネルギー
$A_\text{GB}$ : 粒界面の断面積

式の分母にある「2」は、シミュレーションモデルが周期的境界条件で作成されており、その中に2つの粒界が含まれるためです。

また、エネルギー的に最も安定な粒界構造を得るため、2段階の探索で構造最適化を行います。まず、粒界面に垂直な方向（c軸）に2つの結晶粒を動かして最適な分離距離を決定し、次にその距離を保ったまま粒界面に平行な方向（a,b軸）で最もエネルギーが低くなる配置を探します。

計算モデルと計算条件#

計算モデルとして、アルミニウムの面心立方格子(FCC)構造におけるΣ3 (111)ねじり粒界(24個原子モデル)を作成しました。モデル作成には、Advance/PHASEに同梱されているPythonライブラリpymatgen [1] の粒界生成機能を利用しました。最適化計算によって得られた安定構造を図1に示します。

高精度な粒界エネルギーを算出するため、比較対象となるバルクエネルギー( $E_\text{bulk}$ )は、粒界モデルと同じ計算条件下で、24層の(111)面を持つ理想結晶セル(図1下)を用いて精密に計算しました。

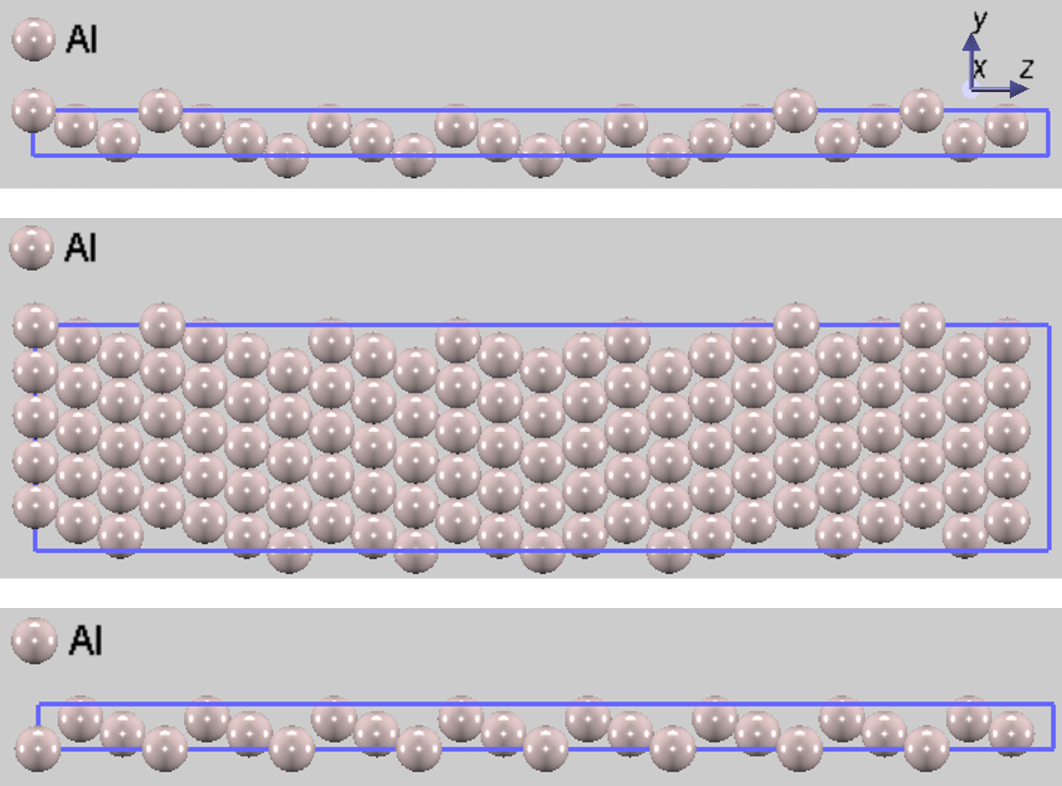
Σ3 (111) twist結晶粒界の計算セル
図1.　最適化後の計算モデル。(上) Al Σ3 (111)ねじり粒界の計算セル。(中) 構造を視認しやすくするための5x5x1スーパーセル。(下) バルクエネルギー計算に用いる(111)面方位を持つ理想結晶セル。

本解析で用いた主な計算条件は表1に示されています。

表1.　計算条件の概要

項目	設定
擬ポテンシャル	ノルム保存擬ポテンシャル
交換相関汎関数	GGA (PBE)
波動関数のカットオフエネルギー	25 Rydberg (約340 eV)
k点サンプリング	11x11x1

計算結果と考察#

粒界エネルギーの比較#

本手法で計算した粒界エネルギー( $\gamma_\text{GB}$ )を、異なる研究グループによる文献値と比較しました（表2）。

表2.　Al Σ3 (111)ねじり粒界エネルギー: 本計算と文献値の比較 (単位: J/m²)

	本計算値	文献値 [2]	文献値 [3]
粒界エネルギー ( $\gamma_\text{GB}$ )	0.042	0.052	-0.004

本計算で得られた粒界エネルギー 0.042 J/m² は、文献値 [2] の 0.052 J/m² と良好な一致を示しています。

一方で、文献値 [3] は -0.004 J/m² という物理的にありえない負の値となっています。これは、この文献が多数の金属・粒界を網羅的に計算する「ハイスループット計算」という手法を用いているためです。AlのΣ3(111)粒界のエネルギーは、理論的にゼロに極めて近い正の値であることが知られています。このような場合、計算の目標精度（この文献では±0.05 J/m²）よりも真の値が小さいため、計算結果が誤差の範囲で負の領域に振れてしまうことがあります。本解析のような個別テーマに特化した計算では、このような問題は生じにくく、より物理的に妥当な値が得られていることがわかります。

Work of Separationの評価#

粒界の破壊に対する抵抗を示す指標として、Work of Separation ( $W_\text{sep}$ ) があります。これは、粒界を2つの自由表面に引き剥がすために必要なエネルギーであり、以下の式で定義されます。

$W_\text{sep} = 2\gamma_\text{surf} - \gamma_\text{GB}$

ここで $\gamma_\text{surf}$ は、粒界が破壊されたときに新たに形成される表面のエネルギーです。別途計算したAl(111)面の表面エネルギー(0.796 J/m²) [4] と、今回得られた粒界エネルギーを用いて $W_\text{sep}$ を算出し、文献値と比較しました（表3）。

表3. Work of Separation ( $W_\text{sep}$ ) の比較 (単位: J/m²)

	本計算値	文献値 [3]
Work of Separation ( $W_\text{sep}$ )	1.55	1.595

算出された $W_\text{sep}$ は 1.55 J/m² となり、文献値の 1.595 J/m² と非常によく一致しています。これにより、本解析で得られた粒界エネルギーの信頼性がさらに裏付けられました。

まとめ#

本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、AlのΣ3(111)ねじり粒界の物性値を評価しました。計算された粒界エネルギー (0.042 J/m²) および Work of separation (1.55 J/m²) は、文献値と良好な一致を示し、計算手法の妥当性を確認しました。また、異なる計算アプローチ（ハイスループット計算と個別テーマ計算）によって生じる結果の違いを考察し、目的に応じた計算手法の選択の重要性を示しました。第一原理計算は、粒界のような複雑な界面の特性を原子レベルで解明し、材料開発に貢献する強力なツールです。

参考文献#

S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. Chevrier, K. A. Persson, and G. Ceder, "Python Materials Genomics (pymatgen) : A Robust, Open-Source Python Library for Materials Analysis", Comp. Mater. Sci. 68, 314 (2013).
X. Pang, N. Ahmed, R. Janisch, and A. Hartmaier, "The mechanical shear behavior of Al single crystals and grain boundaries", J. Appl. Phys. 112, 023503 (2012).
H. Zheng, X. G. Li, R. Tran, C. Chen, M. Horton, D. Winston, K. A. Persson, and S. P. Ong, "Grain boundary properties of elemental metals", Acta Materialia 186, 40 (2020).
第一原理計算によるAl表面エネルギーの評価