第一原理計算によるAl表面エネルギーの評価#

固体材料の表面は、内部の原子に比べて結合相手が少ないため、エネルギー的に不安定な状態にあります。この余剰なエネルギーが「表面エネルギー」であり、結晶成長、触媒活性、濡れ性といった材料の様々な特性を支配する重要な物理量です。本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、面心立方格子(FCC)金属であるアルミニウム(Al)の主要な低指数面である(100)、(110)、(111)面の表面エネルギーを計算し、その相対的な安定性を評価しました。
Keywords: 第一原理計算, DFTシミュレーション, 表面エネルギー, スラブモデル, アルミニウム, 線形フィッティング法
計算方法#
固体の表面エネルギーを計算する手法として、「従来法」と「線形フィッティング法」の2つがありました。
従来法#
スラブモデルの全エネルギー()、バルク(内部)の原子あたりのエネルギー()、表面積()を用いて、表面エネルギー()は以下の式で算出されます。
ここで、 はスラブモデルに含まれる原子数です。この手法は、との計算間のわずかな誤差により、スラブの層数を増やしても計算値が収束しにくいという問題があります。
線形フィッティング法#
この収束性の問題を解決するため、より高精度な「線形フィッティング法」を本解析では主として採用しました [1]。この手法では、層数 に対してスラブの全エネルギーが線形に変化することを利用し、その切片から表面エネルギーを精度良く算出します。
計算モデルと計算条件#
Alのバルク結晶(最適化した格子定数 4.042 Å)から、(100), (110), (111)の各表面を持つスラブモデルを作成しました。各モデルは、真空層を15 Å以上確保し、周期的境界条件を適用しています。表面エネルギーの層数依存性を評価するため、複数の層数を持つモデル(7層から19層)を用意しました。構造最適化の際には、スラブ内部がバルクの性質を保つようスラブ中心の3層を固定し、それ以外の原子を可動にして原子座標の緩和を行いました。
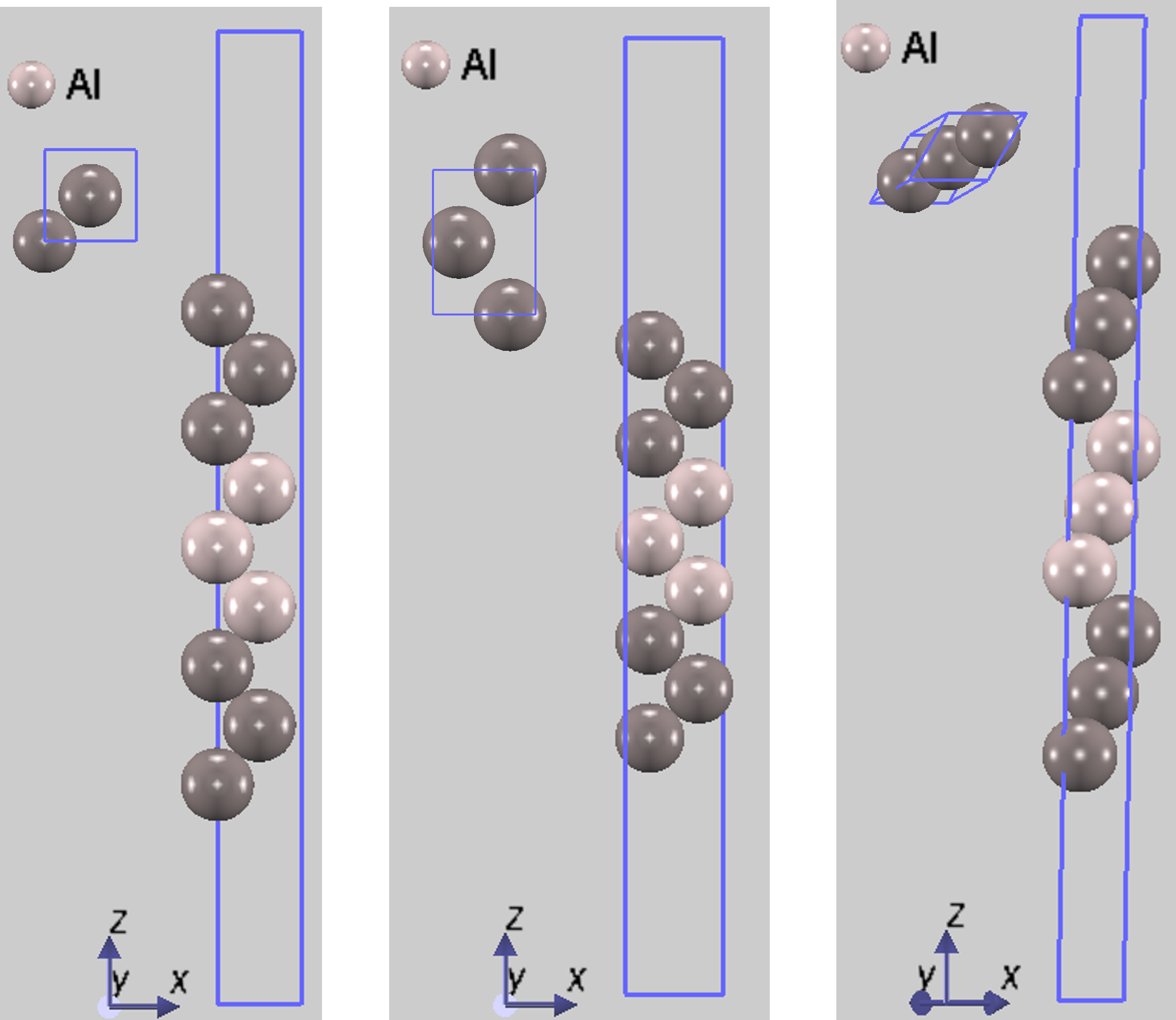
図1. (左から) Al(100), Al(110), Al(111)の計算に用いたスラブモデルの例。スラブ中心の3層を固定して、ほかのdarker colorで示す原子を可動に設定しています。
スラブモデルの対称性について#
表面エネルギーの計算では、スラブの上下で構造が異なることに起因する人工的な双極子(ダイポール)の発生を防ぐため、対称性を持つスラブモデルを用いることが重要です。ここで注意すべきは、「対称性」には2種類ある点です。
- 鏡面対称: スラブ中心の平面に対して、上下が鏡写しの関係になる対称性。図1のAl(100)や(110)面はこの対称性を持ちます。
- 点対称(反転対称): スラブ中心の点に対して、すべての原子が対になる原子を持つ対称性。
図1のAl(111)面はABCABC...という積層構造をとるため、厳密な鏡面対称を持ちません。しかし、スラブ中心に反転中心が存在するため、点対称性を持ちます。点対称性があればスラブ全体の双極子モーメントはゼロになるため、Al(111)スラブはエネルギー計算に適した有効な「対称モデル」と見なすことができます。本解析で用いたモデルはAdvance/PHASEに同梱したpymatgen [2, 3] で用いて、symmetrize=Trueという条件で作成したものであり、すべてこの条件を満たしています。
本解析で用いた主な計算条件は表1に示されています。
表1. 計算条件の概要
| 項目 | 設定 |
|---|---|
| 擬ポテンシャル | ノルム保存擬ポテンシャル |
| 交換相関汎関数 | GGA (PBE) |
| 波動関数のカットオフエネルギー | 25 Rydberg (約340 eV) |
| k点サンプリング | 表面に応じて11x8x1から11x11x1に設定 バルク:8x8x8 (conventional cell) |
計算結果と考察#
従来法による表面エネルギーの層数依存性#
はじめに、従来法で計算した表面エネルギーの層数依存性を示します。図2〜4が示すように、いずれの表面においても、スラブの層数を増やしても表面エネルギーは特定の値に収束せず、値が層数によって変動しています。これは、手法に起因する系統的な誤差の存在を示唆しています。
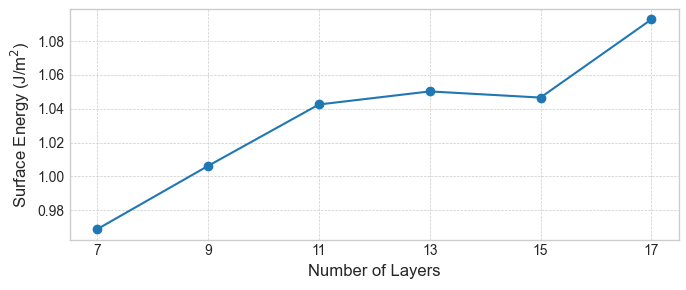
図2. 従来法によるAl(100)表面エネルギーの層数依存性。
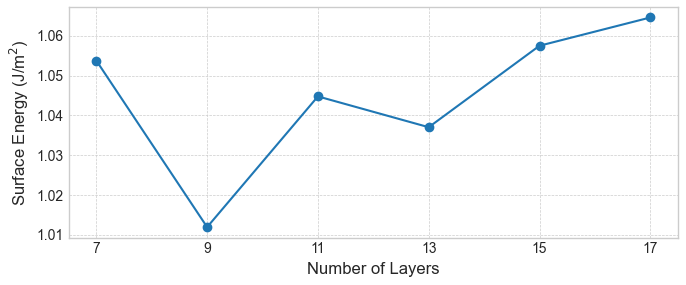
図3. 従来法によるAl(110)表面エネルギーの層数依存性。
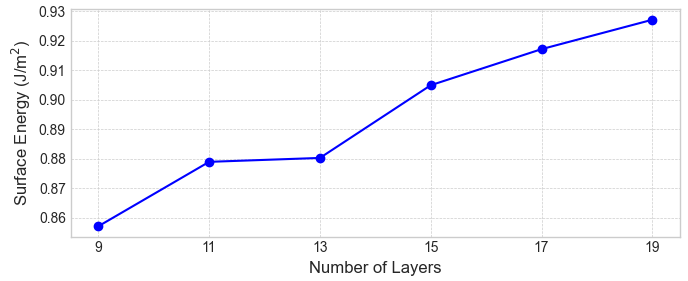
図4. 従来法によるAl(111)表面エネルギーの層数依存性。
線形フィッティング法による収束値の算出#
次に、この収束性の問題を解決するため、線形フィッティング法を適用しました。図5〜7に示す通り、各表面のスラブ全エネルギーは層数に対して非常に良好な直線関係を示し、信頼性の高いフィッティングが可能です。
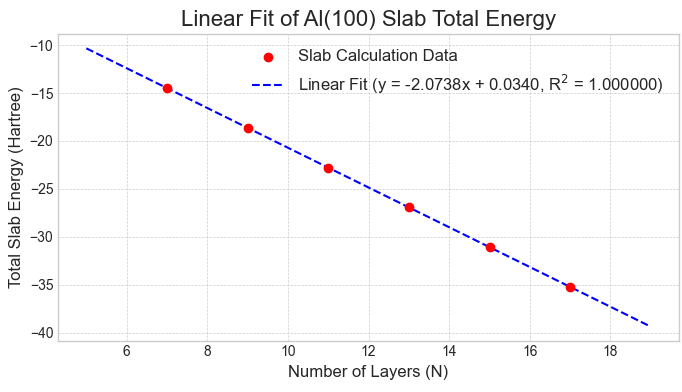
図5. Al(100)スラブの全エネルギーと層数の線形関係。
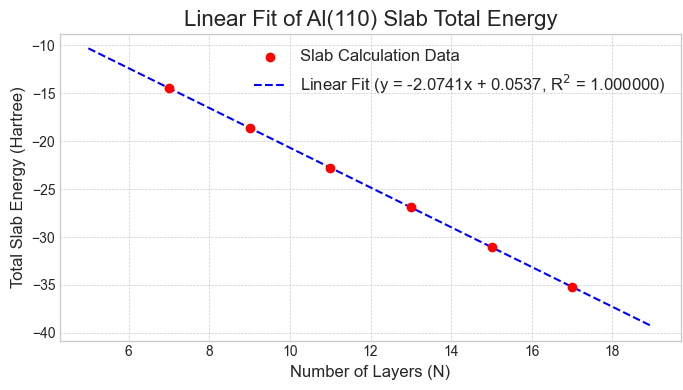
図6. Al(110)スラブの全エネルギーと層数の線形関係。
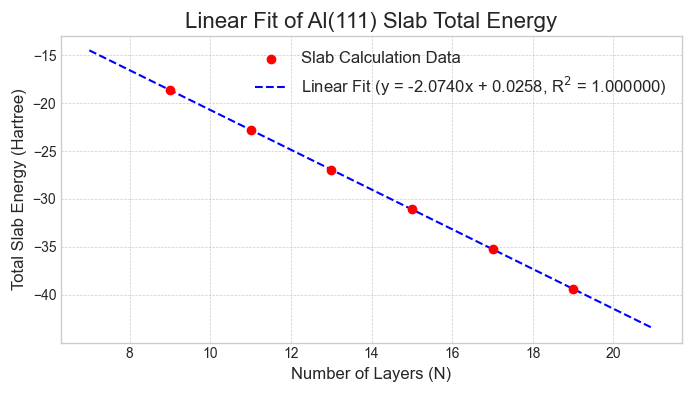
図7. Al(111)スラブの全エネルギーと層数の線形関係。
結果の比較と考察#
線形フィッティング法によって得られた各表面のエネルギーの収束値を、他の理論計算による文献値と比較して表2にまとめます。
表2. Al各表面の表面エネルギー: 本計算と文献値の比較 (単位: J/m2)
| 表面 | 本計算値 (GGA/PBE) | 文献値 [3] (GGA/PBE) |
|---|---|---|
| Al(111) | 0.796 | 0.77 |
| Al(100) | 0.906 | 0.91 |
| Al(110) | 1.014 | 0.98 |
考察:
本計算で得られた表面エネルギーの序列は となりました。これはFCC金属の表面原子密度が (111) > (100) > (110) の順であることと対応しており、原子が密に詰まっている表面ほど安定であるという物理的描像と一致します。
また、同じ交換相関汎関数(GGA/PBE)を用いた他の理論研究[3]と比較すると、すべての表面で非常に近い値が得られました。この文献値との良好な一致は、本解析で採用した計算条件と線形フィッティング法が妥当であり、信頼性の高い結果を与えていることを裏付けています。
補足:従来法と線形フィッティング法の値が異なる理由#
図2〜4で示したように、従来法で計算した最も厚いスラブの値は、線形フィッティングで得られた収束値(表2)よりも常に高くなりました。この理由は、従来法で用いる「バルク計算のエネルギー()」と、スラブ計算と真に整合性のとれた「スラブ内部のエネルギー()」との間に、ごくわずかな差があるためです。
従来法の計算式は、このエネルギー差()の影響を受けるため、近似的に以下のように書き換えられます。
この の差は、3次元周期のバルク計算と2次元周期のスラブ計算における実効的なk点サンプリングの不一致などが原因と考えられます。今回のAlの計算では、すべての表面でがわずかに正の値でした。そのため、右辺第二項の誤差項は層数()に比例して正の方向に増加し、従来法で計算した最も厚いスラブの値が真の収束値 () を上回る原因となります。このことからも、精密な表面エネルギー計算における線形フィッティング法の優位性がわかります。
まとめ#
本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、Alの(100), (110), (111)面の表面エネルギーを評価しました。従来法ではスラブの層数に対して表面エネルギーが収束しない問題を確認しましたが、線形フィッティング法を適用することで、信頼性の高い収束値を得ることができました。算出された表面エネルギーの序列は であり、表面原子密度に基づく物理的な予測や他の理論計算結果とも一致しています。これは、第一原理計算が材料表面の基本的な物性を解明・予測する上で強力なツールであることを示しています。
本解析の詳細や、研究への適用可能性に関するご相談はこちら
お問い合わせ参考文献#
- V. Fiorentini and M. Methfessel, "Extracting convergent surface energies from slab calculations", J. Phys.: Condens. Matter 8, 6525 (1996).
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. Chevrier, K. A. Persson, and G. Ceder, "Python Materials Genomics (pymatgen) : A Robust, Open-Source Python Library for Materials Analysis", Comp. Mater. Sci. 68, 314 (2013).
- R. Tran, Z. Xu, B. Radhakrishnan, D. Winston, W. Sun, K. A. Persson, and S. P. Ong, "Surface energies of elemental crystals", Sci. Data 3, 160080 (2016).
関連ページ#
- 第一原理計算ソフトウェア Advance/PHASE
- 解析分野:ナノ・バイオ
- 産業分野:材料・化学