非平衡グリーン関数法(NEGF)との連携による微小電界放出電流の第一原理計算#

PHASE logo

電界放出（Field Emission）電流の予測において、第一原理計算による原子スケールのポテンシャル障壁評価は不可欠です。しかし、得られたポテンシャルからトンネル電流を算出する際、標準的に用いられるWKB近似（半古典的近似）では、ナノスケールの界面における量子力学的な反射や干渉効果を無視してしまうため、定量的な信頼性に課題が残ります。本事例では、第一原理計算ソフトウェアAdvance/PHASEに実装されている有効遮蔽媒質（ESM）法を用いて算出した高精度な静電ポテンシャル $V(z)$ を入力データとし、非平衡グリーン関数法（NEGF: Non-Equilibrium Green's Function method）を用いることで、空間電荷効果が無視できる微小電流領域（デバイスの漏れ電流や立ち上がり特性など）におけるトンネル確率と電流密度を算出しました。原子スケールの急峻なポテンシャル変化を考慮した本手法と、従来のWKB近似の結果を比較することで、界面反射が電流値に与える影響（WKB近似の過大評価傾向）を定量的に評価しています。

Keywords: 第一原理計算, DFTシミュレーション, ESM法, 非平衡グリーン関数 (NEGF), トンネル電流, 漏れ電流, リーク電流, WKB近似, 透過係数, 微小電界放出, Al(100)

計算フローと解析手法#

本解析は以下の2段階のステップで構成されています。

ESM法によるポテンシャル計算 (DFT):
帯電スラブモデル（Al(100)突起構造）に対してESM法 [1] を用いて自己無撞着計算を行い、外部電場下での静電ポテンシャルプロファイル $V(z)$ を取得します [2]。
NEGF法による輸送特性計算 (Python script):
得られた $V(z)$ を1次元散乱問題として解き、透過係数 $T(E)$ および電流密度 $J$ を算出します。

1. WKB近似#

比較のために用いたWKB (Wentzel-Kramers-Brillouin) 近似 [3] では、ポテンシャル障壁が滑らかに変化すると仮定し、以下の式で透過係数 $T_{\text{WKB}}(E)$ を見積もります。

$T_{\text{WKB}}(E) = \exp \left( -2 \int_{z_1}^{z_2} \sqrt{\frac{2m^*(V(z) - E)}{\hbar^2}} dz \right)$

ここで、 $z_1, z_2$ は古典的転回点（ $V(z)=E$ となる位置）です。WKB法は計算が簡便ですが、界面での波動関数の接続を考慮しないため、反射効果を記述できません。

2. 非平衡グリーン関数法 (NEGF) の概要#

NEGF法 [4] では、以下の手順で量子力学的な散乱問題を厳密に解きます。

(a) ハミルトニアンの構築#

電子の有効質量 $m^*$ を用いた1次元有効質量ハミルトニアン $H$ を、位置 $z$ を離散化して構築します。

$H = -\frac{\hbar^2}{2m^*} \frac{d^2}{dz^2} + V(z)$

(b) グリーン関数の計算#

エネルギー $E$ に対する遅延グリーン関数 $G^R(E)$ を計算します。ここで、 $\Sigma_L, \Sigma_R$ はそれぞれ左電極（金属）および右電極（真空）との結合を表す自己エネルギー項であり、開放境界条件（Open Boundary Condition）を記述します。

$G^R(E) = \left[ E I - H - \Sigma_L(E) - \Sigma_R(E) \right]^{-1}$

(c) 透過係数の算出#

得られたグリーン関数を用いて、フィッシャー・リー (Fisher-Lee) の公式より透過係数 $T_{\text{NEGF}}(E)$ を求めます。

$T_{\text{NEGF}}(E) = \text{Trace} \left[ \Gamma_L G^R \Gamma_R G^{R\dagger} \right]$

ここで、 $\Gamma_{L/R} = i(\Sigma_{L/R} - \Sigma_{L/R}^\dagger)$ は準位幅関数（Broadening function）です。

(d) 電流密度の算出#

最後に、有限温度 $T$ における電流密度 $J$ を、Supply Function Modelを用いて積分計算します。

$J = \frac{e m^* k_B T}{2\pi^2 \hbar^3} \int_{-\infty}^{\infty} T(E) \ln \left( 1 + \exp \left( \frac{E_F - E}{k_B T} \right) \right) dE$

計算条件#

表1. 輸送計算パラメータ

項目	設定
入力ポテンシャル	ESM法により算出されたAl(100)突起表面の $V(z)$
温度	300 K
*有効質量 $m^$**	1.0 $m_e$ (自由電子近似)
エネルギー範囲	$E_F - 1.5 \text{ eV}$ ～バリア頂点 $+ 1.0 \text{ eV}$

解析結果と考察#

1. Al(100)突起表面のポテンシャルプロファイル：文献との比較#

Al(100)突起表面（4原子+1原子）[2] に対して過剰電子（ $q=-0.4e$ ）を与え、外部電場を誘起させた状態でESM法計算を行いました。図1に得られた自己無撞着な静電ポテンシャルプロファイルを示します。

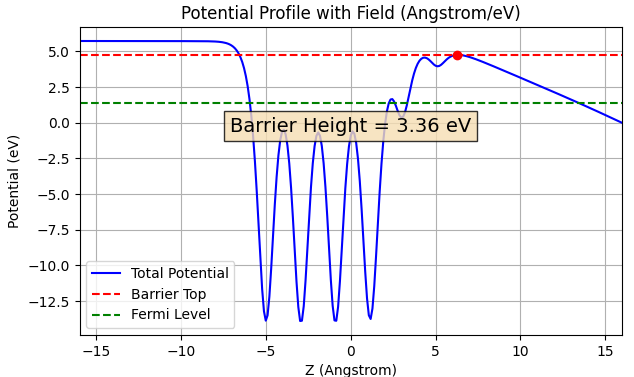
全ポテンシャルプロファイル・ポテンシャル障壁
図1.　ESM法で得られたポテンシャルプロファイル（遠方電場勾配: -0.543 V/Å）。バリアハイト $\Phi_B = 3.36 \text{ eV}$ 。

外部電場 $F$ = 5.43 V/nm (5.43 V/Å)下において、フェルミ準位（ $E_F$ ）に対する実効的なポテンシャル障壁高さ $\Phi_B$ は 3.36 eV と算出されました。この値の妥当性を検証するため、Gohdaらによる散乱理論DFTを用いた先行研究 [5] と比較を行います。

文献値からの推算: Gohdaらの報告（Fig. 3(c)）によれば、電界 $F$ = 10 V/nm における局所的な障壁低下量は、5原子突起で約2.24 eV、14原子突起で約3.42 eVです。また、14原子突起における電界依存性（ $F$ = 10 $\to$ 5 V/nm で障壁が約1.77 eV上昇）を考慮し、5原子突起においても同様の傾向を示すと仮定します。この仮定に基づき $F$ $\approx$ 5 V/nm時の障壁高さを推算すると、約 3.23 eVとなります。
比較結果: 本解析で得られた 3.36 eVは、推算値（3.23 eV）に近い値を示しました。トンネル確率は障壁高さに対して指数関数的な感度を持つため、0.13 eVの差異は電流値の絶対値評価において無視できない影響（オーダーの違い）を与え得ますが、文献と同様に仕事関数からの大幅な障壁低下が見られることから、ESM法は原子突起によるポテンシャル変調効果を物理的に矛盾なく記述できていると言えます。

2. 透過係数とエネルギー分解電流スペクトル#

図2に、本解析で得られたポテンシャルプロファイル、透過係数 $T(E)$ 、電流密度スペクトル $dJ/dE$ を示します。図3に電流密度スペクトルの拡大図を示します。

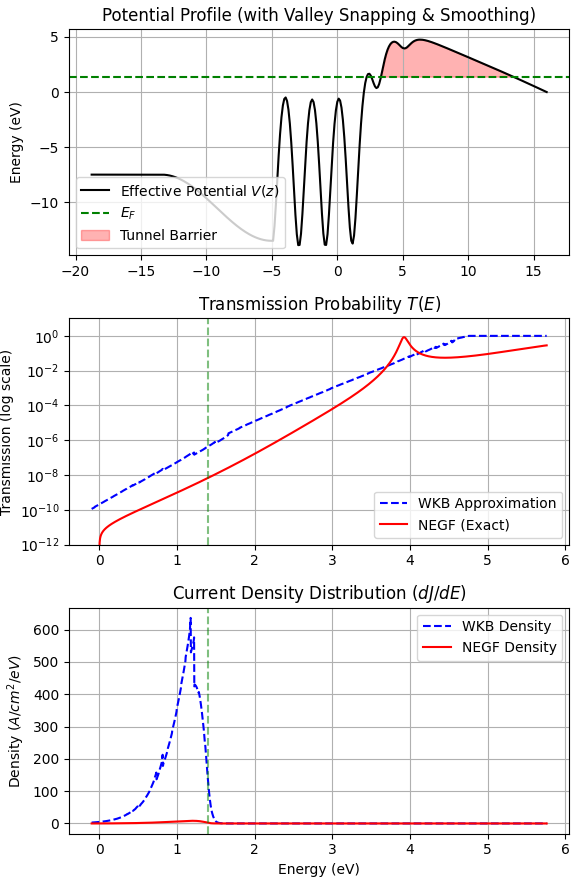
計算結果: ポテンシャル、透過係数、電流スペクトルの比較
図2.　(上) ESM法で得られたポテンシャル $V(z)$ とトンネル障壁領域（赤色）。(中) NEGF法(赤実線)とWKB近似(青破線)による透過係数 $T(E)$ の比較。(下) 電流密度へのエネルギー別寄与（Current Density Spectrum）。

Zoomed NEGF Current Density Spectrum
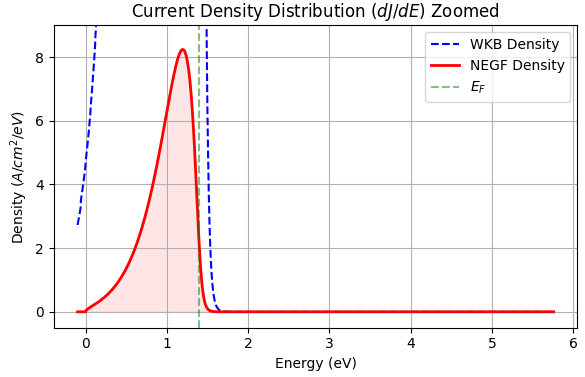
図3.　電流密度スペクトルの拡大プロット。

※計算モデルの境界条件（Bulk Connection）について

第一原理計算で得られるポテンシャルデータは有限の計算領域に限られますが、輸送計算（NEGF）においては左側の領域が「電子を無尽蔵に供給できる金属（リザーバ）」として機能する必要があります。そのため、本解析ではポテンシャル $V(z)$ の左端（金属内部側）について、原子層奥のポテンシャルの谷底を基準としたバルク接続（Bulk Connection）処理を行っています。これにより、フェルミ準位以下の電子状態が正しく定義され、物理的に妥当な電流供給がシミュレートされます。

透過係数の乖離: フェルミ準位（ $E_F$ 、緑点線）近傍のエネルギー領域において、NEGF法による厳密解（赤実線）は、WKB近似（青破線）と比較して1桁〜2桁低い値を示しています。
電流スペクトル: 電流密度のピークは $E_F$ の直下（約 $E_F-0.2 \text{ eV}$ ）に位置しています。これは「エネルギーが高いほど透過しやすい」効果と「高エネルギー側の占有電子数が減少する（フェルミ分布）」効果の競合によるもので、物理的に妥当な振る舞いです。なお、透過係数(NEGF)において 3.9 eV 付近に見られるピークはポテンシャル井戸内の共鳴準位に由来しますが、 $E_F$ より遥かに高エネルギーであるため電流には寄与しません。

3. WKB近似の過大評価と量子反射効果の重要性#

エネルギー積分により得られた総電流密度 $J$ を比較すると、以下の結果となりました。

$J_{\text{WKB}} = 2.67 \times 10^2 \text{ A/cm}^2, \quad J_{\text{NEGF}} = 4.79 \times 10^0 \text{ A/cm}^2$ $\text{Ratio} \ (J_{\text{NEGF}} / J_{\text{WKB}}) \approx 0.018$

なぜ NEGF の結果は WKB の約 1/56 にまで低下したのか？

この顕著な差異（Ratio $\approx$ 0.018）は、原子スケールの急峻なポテンシャル変化に伴う量子力学的な反射効果に起因しています。

波動インピーダンスの不整合: 図2(上)に見られるように、表面付近（$Z \approx 0 \sim 5 \text{ Å}$）のポテンシャルは原子核位置に対応して急激に振動しています。WKB近似はポテンシャルが電子波長に対して滑らかに変化することを前提としますが、このような原子スケールの急峻な界面では電子波の反射（波動インピーダンス不整合）が強く生じます。
Pre-factor（前係数）の減少: 厳密な量子力学（NEGF）では、界面での波動関数の接続条件により透過係数に 1 未満の前係数（Pre-factor）が現れますが、単純なWKB則はこの効果を無視（係数=1と仮定）するため、透過率を過大評価します。

この結果は、Kyritsakisらによる近年の研究報告 [6] とも整合します。彼らはナノスケール（半径3nm）のエミッタにおいて、厳密な数値計算結果が平面近似に基づく標準理論（GTF/WKB）よりも最大で27倍小さくなることを報告しています。本解析で得られた約56倍という乖離も、同様の幾何学的・量子力学的効果による物理的に妥当な結果と言えます。

以上の知見は、微細デバイス設計において従来のWKB則（Fowler-Nordheim式）を安易に適用することのリスクを示唆しています。高精度な設計を行う上では、本事例で示されたような約1/50程度の補正係数を導入するか、あるいは本手法のような第一原理輸送計算を適用することが不可欠です。

4. 解析の適用範囲と工学的価値#

本解析は1次元モデルを採用しているため、電子の横方向への閉じ込め効果や3次元的な散乱効果は考慮されていません。より厳密な電流値予測にはAtomistic NEGF法が必要となりますが、本事例の主眼は、原子スケールの急峻なポテンシャル変化に対し、従来のWKB近似がどのように破綻するかを定量的に示す点にあります。

本手法の適用にあたっては、以下の物理的妥当性と数値計算上の制約に留意する必要があります。

固定ポテンシャル近似の妥当性#

本解析では、電流の流出に伴うポテンシャル形状の緩和を無視する「固定ポテンシャル近似」を採用しています。一般に、放出電子の空間電荷がポテンシャルに無視できない影響を与え始める（近似が破綻する）電流密度の閾値は $10^6 \sim 10^7 \text{ A/cm}^2$ 程度とされています [7]。本解析で得られた電流密度は約 $4.8 \text{ A/cm}^2$ であり、この閾値を大幅に下回っています。したがって、静的なESMポテンシャルを用いて輸送特性を算出する本手法は、対象とする微小電流領域において物理的に妥当であり、界面反射効果（WKB近似との乖離）を正しく評価していると言えます。

ESM法の収束性と電子のスピルアウト（Electron Spilling）#

本手法は、ESM法により算出された静電ポテンシャルプロファイル $V(z)$ を入力データとします。しかし、電界電子放出が生じるような強電界条件下では、第一原理計算（DFT）の過程で電子が真空領域へ過剰に漏れ出すため、SCF（自己無撞着場）計算が収束しなくなる問題（電子のスピルアウト、あるいはトンネル効果による不安定性）が生じ得ます。ESM法の計算が収束しない領域では本手法も適用できず、低電界の結果から強電界時のポテンシャルを外挿することも困難です。そのため、本手法の適用範囲は、ESM法による構造最適化およびSCF計算が正常に収束する電界強度範囲内に限定されます。

まとめ#

本事例では、第一原理計算ソフトウェアAdvance/PHASEのESM法と、PythonによるNEGF法解析を連携させ、Al(100)原子スケール突起からの微小電界放出電流を評価しました。解析にあたっては、ESM法が先行研究と同様に原子突起によるポテンシャル障壁の変調（低下）効果を適切に再現していることを確認し、さらに金属側ポテンシャルのバルク接続処理を行うことで、物理的に妥当な電子リザーバを定義しました。その結果、現実的な動作電界（5.43 V/nm）下において、NEGF法で算出した電流値は、WKB近似値の約1.8%（約1/56）に留まることが明らかとなりました。この大幅な電流低下は、原子レベルの急峻な界面での量子反射に起因するものです。ナノスケールエミッタの設計において、従来の半古典的近似（WKB）は電流値を過大評価する可能性が高く、第一原理計算に基づく輸送特性評価が重要であることが実証されました。（注：本手法の適用範囲は、ESM法の計算が収束する電界強度領域に限定されます。）

本解析の詳細や、研究への適用可能性に関するご相談はこちら

お問い合わせ

参考文献#

M. Otani and O. Sugino, "First-principles calculations of charged surfaces and interfaces: A plane-wave nonrepeated slab approach", Phys. Rev. B 73, 115407 (2006).
帯電金属表面突起によるポテンシャル障壁変調の第一原理計算
R. H. Fowler and L. W. Nordheim, "Electron Emission in Intense Electric Fields", Proc. R. Soc. London A 119, 173 (1928).
S. Datta, Electronic Transport in Mesoscopic Systems, Cambridge University Press, Cambridge (1995).
Y. Gohda and S. Watanabe, "Theoretical analysis of field emission from atomically sharp aluminum tips", Surf. Sci. 516, 265 (2002).
A. Kyritsakis and J. P. Xanthakis, "Extension of the general thermal field equation for nanosized emitters", J. Appl. Phys. 119, 045303 (2016).
J. P. Barbour, W. W. Dolan, J. K. Trolan, E. E. Martin, and W. P. Dyke, "Space-charge effects in field emission", Phys. Rev. 92, 45 (1953).