帯電金属表面突起によるポテンシャル障壁変調の第一原理計算#

電界放出ディスプレイや電子顕微鏡の電子源、さらには真空ナノエレクトロニクスデバイスにおいて、金属表面からの電子放出特性を制御することは極めて重要です。電子放出効率は表面のポテンシャル障壁(仕事関数を含む)に強く依存しますが、これは表面形状や印加電場の影響を複雑に受けます。しかしながら、通常の周期的スラブモデルを用いた第一原理計算では、外部電場を印加すると静電ポテンシャルが発散してしまうため、帯電状態や有限電場下での精密な解析は困難でした。本事例では、第一原理計算ソフトウェアAdvance/PHASEに実装されている ESM (Effective Screening Medium) 法を用いることで、外部電場下にあるAl(100)表面のポテンシャル障壁を計算し、原子レベルの微小な突起構造が局所的な電界集中を引き起こしてポテンシャル障壁を低下させる様子を定量的に評価しました。
Keywords: 第一原理計算, DFTシミュレーション, ESM法, 仕事関数, ポテンシャル障壁, 電界放出, 局所電界集中効果, 表面構造, Al(100)
計算手法:ESM法による電場印加#
本解析では、系に過剰電子を与え、表面垂直方向に外部電場が印加された状況を記述するためにESM法 [1] を採用しました。通常のスラブモデル(3次元周期境界条件)では、系を帯電させるとクーロン相互作用の総和が発散してしまいますが、ESM法ではセルの一方向(Z方向)の境界条件を開放し、そこに「有効遮蔽媒質」を配置することで、孤立スラブに対する帯電計算を厳密に行うことが可能です。今回は、スラブの片側に真空領域を、もう片側に理想的な金属領域を配置する「真空/スラブ/金属 (Vacuum/Slab/Metal)」の境界条件を採用しました。これにより、金属側で電場を遮蔽しつつ、真空側へ染み出す電場(電子放出方向の電場)を適切に記述しています。
計算モデルと条件#
本解析では、計算効率と精度のバランスを考慮した代表的なAl(100)スラブモデル(4層、4x4スーパーセル)を採用しました。清浄なAl(100)表面(フラット)と、表面に原子突起(4原子+1原子)を設けたモデルの2種類を作成しました。
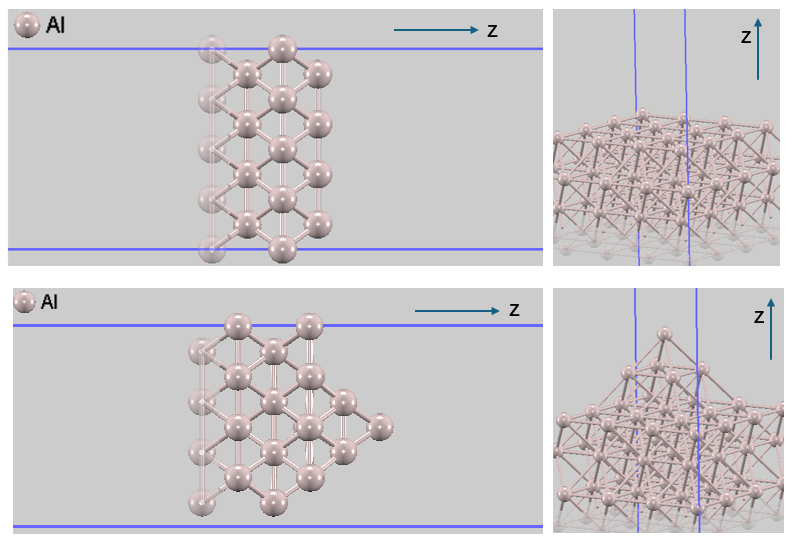
図1. 計算に用いたAl(100)スラブモデルの側面図と斜視図。(上) 清浄表面、(下) 突起構造あり。固定原子層を半透明で表示しています。
表1. 主な計算条件
| 項目 | 設定 |
|---|---|
| 計算手法 | 平面波・擬ポテンシャル法 (DFT) ※ノルム保存型擬ポテンシャル使用 |
| 交換相関汎関数 | GGA (PBE) |
| カットオフエネルギー | 25 Rydberg |
| スラブモデル | Al(100) 4x4スーパーセル, 4層(底面固定) |
| 真空層厚さ | > 20 Å |
| k点サンプリング | 3x3x1 |
| 構造最適化閾値 | 2 x 10-4 Hartree/bohr |
計算結果と考察#
1. Al(100)清浄表面の仕事関数(中性)#
電場を印加する前に、まずは中性状態(過剰電子なし、q=0)におけるAl(100)清浄表面の仕事関数を算出しました。図2にポテンシャルプロファイル(面内平均)を示します。
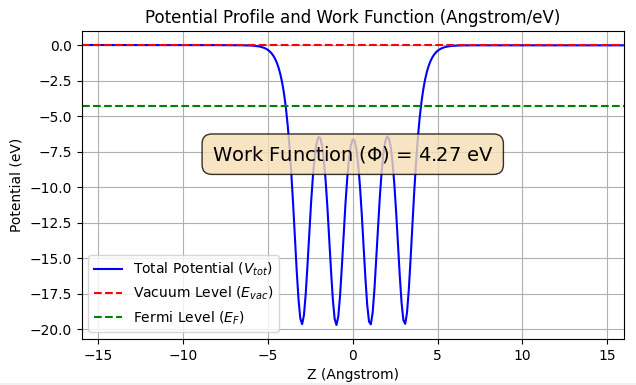
図2. 中性Al(100)表面のポテンシャルと仕事関数。
計算の結果、仕事関数は 4.27 eV と算出されました。Al(100)面の仕事関数の実験値は一般的に 4.20 ~ 4.41 eV 程度(例: 4.20 eV [2])が報告されており、本計算結果は実験値と良い一致を示しています。これにより、用いたモデルと計算条件の妥当性が確認できました。
2. 帯電表面(フラット)におけるポテンシャル障壁#
次に、系に過剰電子(q=0.2e、負に帯電)を与え、外部電場を誘起させた状態の計算を行いました。図3に、Al(100)清浄表面(突起なし)における全ポテンシャルプロファイル(面内平均)を示します。
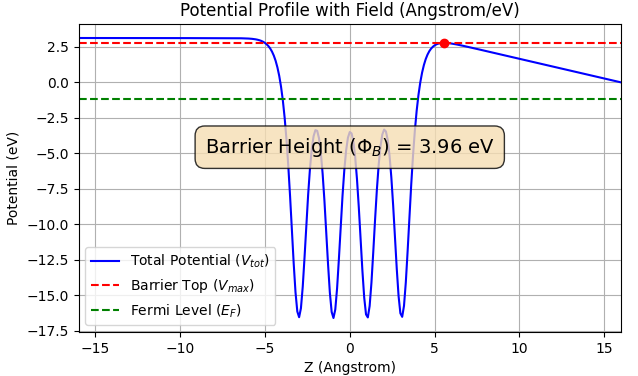
図3. 帯電したAl(100)清浄表面のポテンシャルプロファイル(遠方電場勾配: -0.277 eV/Å)。バリアハイト 。
真空領域でポテンシャルが傾き、外部電場が形成されていることが確認できます。この時の電場勾配は約 -0.277 eV/Å であり、フェルミ準位()から見たポテンシャルの最大値(バリアハイト)は 3.96 eV と算出されました。
3. 突起構造による障壁変調効果#
続いて、同じ量の過剰電子(q=0.2e)を突起構造のある表面に与えた場合の結果を図4に示します。遠方のマクロな誘起電場(ポテンシャル勾配)は清浄表面と同等ですが、突起近傍のポテンシャル形状が大きく変化しています。
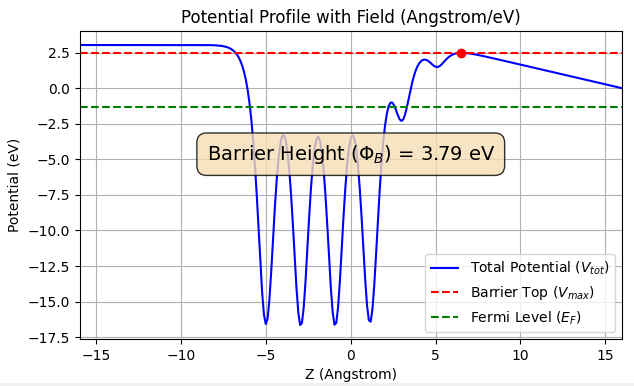
図4. 帯電した突起構造ありAl(100)表面のポテンシャルプロファイル(遠方電場勾配: -0.277 eV/Å)。バリアハイト 。
解析の結果、突起構造がある場合のバリアハイトは 3.79 eV となり、清浄表面と比較して 0.17 eV 低下していることが明らかになりました。これは、以下の要因によるものです。
- 局所電界集中効果 (Lightning rod effect): 原子スケールの突起先端に電荷が集中することで、局所的に電場が強められます [3, 4]。
- ポテンシャルの押し下げ: 強められた局所電場により、電子が感じるポテンシャル障壁が空間的に急峻に押し下げられます。
4. 電荷密度の可視化とメカニズムの解明#
この効果を視覚的に確認するため、フェルミ準位近傍の部分電荷密度分布を可視化しました(図5)。
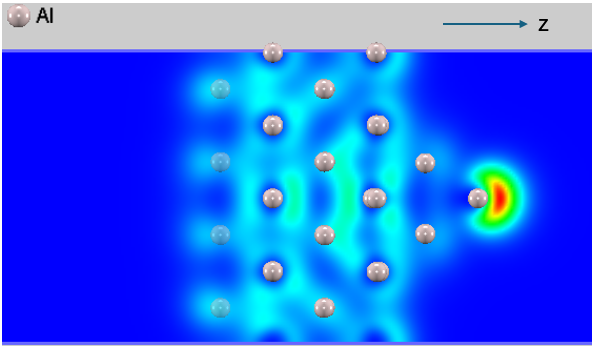
図5. 突起構造周辺の部分電荷密度分布(エネルギー範囲: から まで)。
図5より、突起先端の原子に電子密度が顕著に集中していることが確認できます。この「原子レベルでの避雷針効果」が、マクロな印加電圧を変えることなく、実効的なポテンシャル障壁を低下させ、電子放出確率を増大させる主要因であることを第一原理計算によって直接示しました。
強電場下における有効ポテンシャル算出の理論的妥当性と限界
1. 準安定状態の記述(断熱近似)
DFTは基底状態の理論であるため、トンネル電流が定常的に流れる非平衡状態を直接記述するものではありません。しかし、電子雲の分極(遮蔽)にかかる時間は、電子が障壁を透過する時間スケールに比べて十分に短いため、断熱近似が成立します。本計算では、電子放出が生じる直前の「分極が完了した準安定状態(Quasi-static state)」としての有効ポテンシャルを評価しています。
2. 計算手法の適用限界(変分崩壊の回避)
一様な外部電場下では、無限遠でポテンシャルが発散するため、数学的な基底状態が存在しません。本解析で用いたESM法は、有限の真空領域内で波動関数が十分に減衰する(電子が表面に局在している)範囲においてのみ正当化されます。実際の電界放出が支配的となるような極めて強い電場領域では、ポテンシャル障壁が極端に薄くなり、電子密度が真空領域へ流出(Charge Spilling)するため、DFT計算は収束しなくなります。本解析の結果は、数値的な崩壊が生じる手前の、物理的に妥当とみなせる領域におけるバリア変調効果を評価したものです。
3. 量子輸送計算への接続
本計算で得られたコーン・シャム有効ポテンシャル \(V_{\text{eff}}(\mathbf{r})\) は、多体効果を含む平均場ポテンシャルです。 特に、原子突起のような不均一構造を含む系において、一般的な面内平均ポテンシャルを用いてしまうと、先端に特有の局所的な電界集中効果や障壁低下が空間的に平均化され、評価精度が損なわれる可能性があります。 そのため、これを入力パラメータとして非平衡グリーン関数法(NEGF)へ接続し、トンネル確率や放出電流密度の高精度な評価 [5, 6] を行うにあたっては、平均化されていない3次元ポテンシャル分布 \(V(x,y,z)\) を用いることが、局所障壁の精密な記述において重要となります。
まとめ#
第一原理計算ソフトウェアAdvance/PHASEのESM計算機能を用いることで、外部電場下におけるAl(100)表面のポテンシャル障壁を解析しました。原子レベルの突起構造が存在することで、局所的な電荷集中が生じ、ポテンシャル障壁が清浄表面よりも約0.17 eV低下することを定量的に示しました。このような解析は、電界放出ディスプレイや走査型トンネル顕微鏡(STM)探針など、ナノスケールの形状制御が性能を左右するデバイスの設計指針を得るための有効なものです。
本解析の詳細や、研究への適用可能性に関するご相談はこちら
お問い合わせ参考文献#
- M. Otani and O. Sugino, "First-principles calculations of charged surfaces and interfaces: A plane-wave nonrepeated slab approach", Phys. Rev. B 73, 115407 (2006).
- R. M. Eastment and C. H. B. Mee, "Work function measurements on (100),(110) and (111) surfaces of aluminium", J. Phys. F: Metal Phys. 3, 1738 (1973).
- Y. Gohda and S. Watanabe, "Total energy distribution of field-emitted electrons from Al(100) surface with single-atom terminated protrusion", Phys. Rev. Lett. 87, 177601 (2001).
- C. Hu, Y. Gohda, S. Furuya, and S. Watanabe, "First-principles calculation of vibrational properties of a nanostructure in electric fields", Jpn. J. Appl. Phys. 42, 4639 (2003).
- Y. Gohda, Y. Nakamura, K. Watanabe, and S. Watanabe, "Self-consistent density functional calculation of field emission currents from metals", Phys. Rev. Lett. 85, 1750 (2000).
- T. Frederiksen, M. Paulsson, M. Brandbyge, and A.-P. Jauho, "Inelastic transport theory from first principles", Phys. Rev. B 75, 205413 (2007).
関連ページ#
- 第一原理計算ソフトウェア Advance/PHASE
- 解析分野:ナノ・バイオ
- 産業分野:材料・化学