DFT計算と弾性力学モデルの連携によるベリリウムの特異な構造変形解析#

Advance/PHASE Logo

ベリリウム（Be）は、軽量かつ高剛性という優れた機械的特性を持つ一方で、その毒性や希少性から実験的な検証が容易ではありません。特に、微細な光学部品や宇宙航空機器の設計において、その特異な弾性挙動（極めて低いポアソン比）が及ぼす影響を正確に把握することは極めて重要です。本事例では、第一原理計算ソフトウェア Advance/PHASE を用いた密度汎関数法 (DFT)で算出された弾性定数をマクロな弾性力学モデルへ適用し、一般的な金属材料（アルミニウム合金）との比較を通じて、その幾何学的な安定性と設計上のメリットを定量的に評価しました。本DFT計算との連携事例は、実験が困難な極限環境下や、未知の新規合金開発における構造変形シミュレーションへの適用可能性を示す有用なベンチマークとなります。

Keywords: 第一原理計算, DFT, マルチスケール解析, ベリリウム, ポアソン比, アンチクラスティック曲率, 構造解析

解析手法と連携の指針#

1. 原子スケール：DFTによる弾性定数の算出#

密度汎関数法（DFT）計算により、ベリリウムの六方最密充填（hcp）構造における独立な弾性コンプライアンス定数 $C_{ij}$ を算出しました。実際の材料製品は微細な結晶の集合体（多結晶）であるため、Hillの近似法（Voigt平均とReuss平均の相加平均）を用いて結晶方位による異方性を平均化し、マクロ解析用の等方性材料パラメータであるヤング率 $E$ とポアソン比 $\nu$ を導出しました [1]。なお、実際の製品では製造プロセスによる配向性が生じる場合がありますが、本事例では理想的な等方性多結晶として評価しました。

2. マクロスケール：構造変形の支配方程式#

DFT計算で得られた物性値を、連続体力学に基づく変形モデルに適用しました。本事例では、基礎的な挙動を確認するための「理論式による可視化」と、複雑な応力状態を評価するための「有限要素法（FEM）」の2段階で評価を行っています。

(1) 基本となる構成則（フックの法則）#

等方性弾性体における応力 $\sigma$ とひずみ $\varepsilon$ の関係は、ヤング率 $E$ とポアソン比 $\nu$ を用いて以下のように記述されます [2]。

$\varepsilon_x = \frac{1}{E} [\sigma_x - \nu(\sigma_y + \sigma_z)]$

この式において、ポアソン比 $\nu$ は「荷重方向のひずみに対して、直交方向へどれだけのひずみ（横変形）が誘発されるか」を決定する係数となります。

(2) 基礎理論による検証（板・円柱）#

上記の構成則を簡単な構造形状（板、円柱）の境界条件に適用し、以下の数理モデルに基づいて変形後の座標を算出しました。

① 板の曲げ変形（アンチクラスティック曲面）

板にＸ軸回りの曲率 $\kappa_x$ を与えた場合、ポアソン効果によりＹ軸方向には逆向きの曲率 $-\nu \kappa_x$ が生じます。この際の中立面における垂直変位 $z(x,y)$ は以下の放物面方程式で近似されます。

$z(x,y) = \frac{1}{2} \kappa_x (x^2 - \nu y^2)$

この第2項 $- \nu y^2$ が、 $\nu$ の違いによる反り形状の差異を生み出します。

② 円柱の圧縮変形（半径方向の膨張）

円柱座標系 $(r, \theta, z)$ において、軸方向に圧縮ひずみ $\varepsilon_z$ を与えた際、半径方向のひずみ $\varepsilon_r$ は以下となります。

$\varepsilon_r = - \nu \varepsilon_z$

これにより、半径 $R$ の円柱は $\Delta R = R \cdot \nu \cdot |\varepsilon_z|$ だけ外側へ膨張します（バレル効果）。

(3) 実用的適用：有限要素法（FEM）#

より複雑な構造（穴あき板）の応力状態を評価するため、FEM解析を実施し、以下の仮想仕事の原理に基づく弱形式を離散化して解いています [3]。

$\int_{\Omega} \delta \boldsymbol{\varepsilon}^T \mathbf{D} \boldsymbol{\varepsilon} \, d\Omega = \int_{\Gamma} \delta \mathbf{u}^T \mathbf{t} \, d\Gamma$

ここで、 $\Omega$ は解析領域全体、 $\Gamma$ は表面力が作用する境界を表します。また、 $\delta \mathbf{u}$ は任意の仮想変位、 $\delta \boldsymbol{\varepsilon}$ はその仮想変位に対応する仮想ひずみ、 $\mathbf{t}$ は境界に作用する表面力ベクトル（分布荷重）です。

有限要素法では、領域内を小さな要素に分割し、要素内の任意の変位 $\mathbf{u}$ を形状関数 $\mathbf{N}$ と節点変位 $\mathbf{u}_e$ を用いて以下のように近似（補間）します。

$\mathbf{u} = \mathbf{N} \mathbf{u}_e$

これに伴い、ひずみ $\boldsymbol{\varepsilon}$ は形状関数の微分（勾配）を含むひずみ-変位マトリクス $\mathbf{B}$ を用いて $\boldsymbol{\varepsilon} = \mathbf{B} \mathbf{u}_e$ と表されます。本解析では、 $\mathbf{D}$ にDFT計算値に基づく弾性マトリクスを使用し、各要素の剛性マトリクス $\mathbf{K}_e$ を以下のように数値積分して求めています。

$\mathbf{K}_e = \int_{-1}^{1} \int_{-1}^{1} \mathbf{B}^T \mathbf{D} \mathbf{B} \det(\mathbf{J}) \, d\xi d\eta$

上式において、 $\det(\mathbf{J})$ は物理座標系 $(x, y)$ と計算上の自然座標系 $(\xi, \eta)$ を結びつけるヤコビ行列の行列式（ヤコビアン）であり、座標変換に伴う積分領域の体積（面積）変化を補正しています。これにより、ポアソン効果による複雑な応力場や変形モードを物理的整合性を保ったまま評価しています。

2. 計算条件#

比較対象として一般的なアルミニウム合金を設定しました。アルミニウム合金は、種類や熱処理によって強度が大きく変化する一方、ヤング率（剛性）は純アルミニウムとほぼ同等であり、合金化による変化は軽微です。そこで本解析では、高強度アルミニウム合金を想定した上で、当該材料を単に「Al」と表記します。実設計での優位性を明確にするため、変形比較は「同一ひずみ」ではなく「同一応力（等荷重）」条件で行っています。

表1. 計算条件の比較

材料	ヤング率 $E$ (GPa)	ポアソン比 $\nu$	荷重条件
ベリリウム (Be)	316.4	0.066	200 MPa (引張/圧縮)
アルミニウム (Al)	70.0	0.33	200 MPa (引張/圧縮)

※Beの物性値にはDFT計算による理論値 [1] を、Alには代表的な文献値（高強度アルミニウム合金を想定）を使用しました。DFT値は絶対零度での値であり、室温の実測値とは熱的影響による数%の差異が生じ得ますが、傾向比較には影響しません。

解析結果と考察#

【可視化に関する技術的注記：微小変形と拡大表示について】

実際の金属材料は微小変形領域でのみ線形弾性挙動を示します。そのため、本解析では工学的な整合性を保つため、現実的な微小ひずみ条件下でシミュレーションを行い、その結果得られた微小変位に対して可視化用の拡大係数（Scale Factor）を適用して描画しています。これにより、物理的な矛盾を生じさせることなく、ポアソン比の違いによる変形モードの差異を明確化しています。

1. シート材の曲げ変形（理論形状）#

板厚2 mm の正方形シート材 (100 mm x 100 mm)に一定の曲げ曲率（0.1%）を与えた際の、ポアソン効果によるサドル型（鞍型）変形の比較です（図1）。

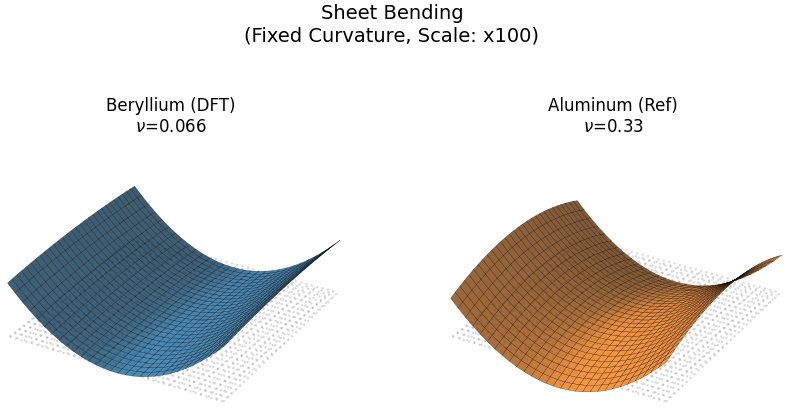
Beryllium and Aluminium Sheet Bending
図1.　シートの曲げ変形解析（Scale: x100）

考察：
図3右のAlに見られる、曲げ軸と直交する方向の「反り」が、Beではほぼ消失しています。この特性は、薄膜ミラーやスキャニングミラーにおいて、不要な光学収差の発生を防ぐ上で重要です。

2. 円柱の圧縮変形（理論形状）#

円柱（半径20 mm, 高さ100 mm）に軸方向から 200 MPa の圧縮荷重を与えた際の変形図です（図2）。変形量は視認性向上のため 300倍に拡大しています。

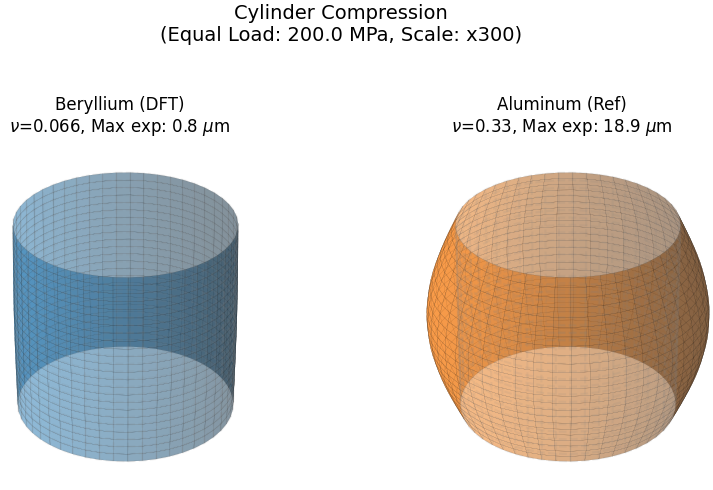
Beryllium and Aluminium Cylinder Compression
図2. 円柱の圧縮変形解析（同一荷重 200MPa, Scale: x300）

考察：
Al（右）は剛性が低いために大きく潰れ（低ヤング率の影響）、さらに高いポアソン比（0.33）により側面が大きく膨らんでいます。対してBe（左）は、高いヤング率により「体積変化（潰れ）」が抑えられ、さらに極めて低いポアソン比により「形状変化（膨らみ）」も最小限に留まっています。

3. 穴あきプレートの引張（FEM解析）#

中央に円孔（半径25mm）を持つプレート（100 mm x 100 mm）をFEM（対称条件を用いた1/4モデル）で解析し、200 MPa 引張時の変形メッシュを描画しました（Scale: x10）。

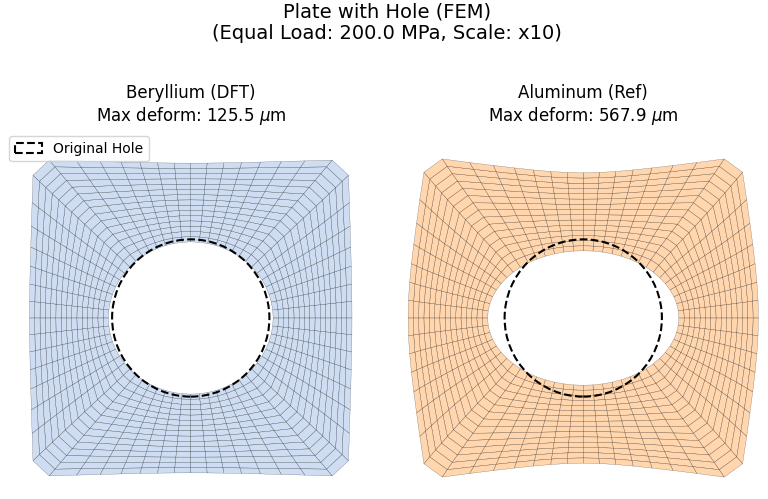
Beryllium and Aluminum Plate Hole Deformation
図3.　穴あきプレートの引張変形解析（同一荷重 200MPa, Scale: x10）

考察：
Al（右）のメッシュを見ると、引張方向（左右）に伸びるだけでなく、ポアソン効果により上下方向に大きく収縮し、中央の穴が楕円形に歪んでいることがわかります。一方、Be（左）はメッシュの歪みが極めて小さく、穴の真円度が高く保たれています。これは「高剛性による変位量の抑制」と「低ポアソン比による横収縮の抑制」の相乗効果であり、幾何公差を維持する必要がある部材にとって決定的な利点です。なお、本解析のような有限幅の板における円孔周辺の応力・変形挙動は、Howlandによる解析解 [4] としても知られており、ポアソン比の違いが穴形状の歪みに顕著な影響を与えるという本FEMの結果は、弾性理論からも支持されます。

※本解析ではPythonによる簡易FEMソルバーを使用しましたが、より複雑な構造解析には Advance/FrontSTR などの専用ソフトウェアが推奨されます。

まとめ#

本解析事例では、第一原理計算ソフトウェアAdvance/PHASEを用いたDFT計算によって導出されたベリリウムの特異な弾性定数（低ポアソン比）が、マクロな構造設計において幾何学的な安定性に寄与することをシミュレーションにより可視化しました。具体的には、ベリリウムを用いることで「曲げ変形時のアンチクラスティック反りの抑制」「圧縮時の膨らみ防止によるクリアランス精度の向上」、そして「引張荷重下での穴の真円度維持」といった幾何学的な安定性が得られることが明らかとなりました。これらの知見は、実験データの乏しい新材料や極限環境材料であっても、DFTを用いた原子スケールの解析からスタートすることで、最終製品における性能優位性や設計リスクを早期かつ定量的に予測可能であることを実証しています。

本解析の詳細や、研究への適用可能性に関するご相談はこちら

お問い合わせ

参考文献#

ベリリウム(Be)の特異な弾性特性のDFT解析
A. E. H. Love, A treatise on the mathematical theory of elasticity, 4th revised edition, Cambridge University Press (2013).
O. C. Zienkiewicz, R. L. Taylor, and J. Z. Zhu, The Finite Element Method: Its Basis and Fundamentals, 6th edition, Elsevier (2005).
R. C. J. Howland, "On the Stresses in the Neighbourhood of a Circular Hole in a Strip under Tension", Philos. Trans. R. Soc. Lond., Ser. A 229, 49 (1930).