第一原理計算での結晶成長シミュレーション:Wulff法を用いたAlナノ粒子の平衡形状予測#

金属ナノ粒子や触媒材料の設計において、結晶の成長を制御し、その平衡形状を知ることは極めて重要です。結晶の形状は、結晶成長の過程で露出する結晶面の安定性(表面エネルギー)によって決定されます。本解析事例では、第一原理計算ソフトウェア Advance/PHASE を用いて算出したアルミニウム(Al)の表面エネルギーに基づき、Wulffの定理(Wulff construction)を適用することで、熱力学的に安定なAl結晶の平衡形状とナノ粒子モデルを予測・構築します。
Keywords: 第一原理計算, DFTシミュレーション, Wulff construction, 結晶成長, 平衡形状, ナノ粒子, 表面エネルギー, アルミニウム(Al)
1. Wulff法(ウルフ法)とは?#
結晶が成長を経て一定の体積を持ちながら平衡状態に達したとき、その形状は「総表面自由エネルギーを最小にする」ように決定されます(Gibbs-Curieの条件)。これを幾何学的に決定する手法が Wulff construction(ウルフの作図)です [1]。
核心的なアイデア:エネルギーと距離の比例関係#
Wulffの定理の核心は、「結晶の中心から各面までの距離 は、その面の表面エネルギー に比例する」という点にあります。
この定理に基づいて作図を行うと、結晶の形状は以下のように決定されます。
- 結晶の中心(原点)から、あらゆる方向の結晶面に対して垂線を引きます。
- その垂線上の、中心から表面エネルギー に比例した距離 の位置に、面に垂直な平面を描きます。
- これら全ての平面で囲まれた領域の最も内側の包絡面(Inner Envelope)が、熱力学的な平衡形状となります。
物理的な解釈#
この幾何学的なルールは、直感的には以下のように理解できます。
- 表面エネルギーが大きい(不安定な)面: 中心からの距離 が遠くなるため、作図において結晶の外側に配置されます。その結果、他の面によって切り落とされ、最終的な形状には現れないか、非常に小さな面積となります。
- 表面エネルギーが小さい(安定な)面: 中心からの距離 が近くなるため、結晶の内側(原点近く)に配置されます。その結果、他の面に切り落とされずに残存し、広く大きなファセットとして現れます。
2. 解析手法とGUIによる操作#
本解析では、以下の手順で形状予測を行いました。
- 第一原理計算による表面エネルギーの評価: Alの主要な低指数面である(100), (110), (111)面について、先行の解析 [2]では、スラブモデルを用いた第一原理計算を行い、表面エネルギーを算出しました。
- Wulff形状の構築: 得られた表面エネルギー値を入力データとして、Wulff法による多面体形状の構築と、それを満たすナノ粒子モデルの作成を行いました。
なお、本解析におけるWulff形状の構築およびナノ粒子モデルの生成には、マテリアルズ・インフォマティクス支援ライブラリである pymatgen [3] および MPInterfaces [4] を活用しています。
GUIによる直感的な操作#
これらの解析機能は、Pythonスクリプトによる自動化はもちろん、ユーザーフレンドリーな GUI (Graphical User Interface) が標準機能として搭載されており、画面上でも実行可能です。図1に示すように、結晶構造ファイルと計算済みの表面エネルギーデータを指定するだけで、手軽に形状予測やナノ粒子モデルの構築を行うことができます。
図1. 形状予測機能のGUI画面。結晶構造ファイルと表面エネルギーデータを指定するだけで解析が可能。
3. 解析結果:Al結晶の平衡形状#
使用した表面エネルギーのデータ(計算値)を表1に示します。
表1. 第一原理計算により得られたAlの表面エネルギー
| 面指数 (Miller Index) | 表面エネルギー (J/m2) |
|---|---|
| (1, 1, 1) | 0.796 |
| (1, 0, 0) | 0.906 |
| (1, 1, 0) | 1.014 |
※ 計算条件:GGA-PBE, Cutoff energy = 25 Ry (詳細はこちらの解析事例)
(A) Wulff Shape(平衡形状)#
表1のエネルギー値を用いて予測されたAlの平衡形状を図2に示します。最もエネルギーが低い (111)面(白色の六角形)が最も広い面積を占め、次にエネルギーが低い (100)面(濃色の四角形)が頂点を切り落とす(Truncate)形で現れています。
なお、(110)面は表面エネルギーが相対的に高いため、今回のWulff作図では結晶内部に埋没し、表面には現れませんでした。その結果、(111)面と(100)面のみで構成される切頂八面体(Truncated Octahedron)に近い形状が形成されています。これは、面心立方格子(FCC)金属の典型的な平衡形状としてよく知られています。
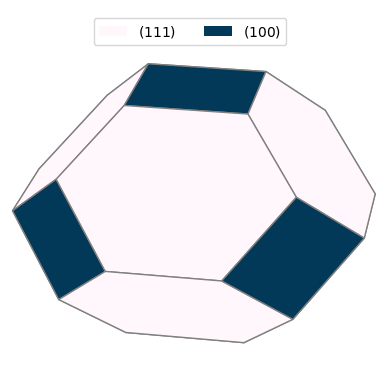
図2. 算出された表面エネルギーに基づくAlのWulff形状。(111)面と(100)面で構成されています。
(B) ナノ粒子モデルの可視化#
上記のWulff形状に基づき、半径15 Å (1.5 nm) のAlナノ粒子モデルを作成した結果が図3です。原子レベルで見ても、(111)面の広いファセットと、頂点付近の(100)ファセットが明瞭に確認できます。

図3. 構築されたAlナノ粒子の原子モデル(半径 15 Å)。図2の多面体形状に対応した原子配列となっています。
さらに、作成したナノ粒子モデルの構造解析(配位数解析)を行った結果(図4)、粒子内部のバルク原子(CN=12)や安定なテラス面の原子(CN=8, 9)に加え、触媒活性点として期待される低配位の原子が多数確認されました。具体的には、面同士が交わるエッジ部分(CN=7)が84個、頂点であるコーナー部分(CN=6)が24個存在し、これら低配位サイト(エッジとコーナーの合計)は108個となり、全原子数の約15%を占めることがわかります。
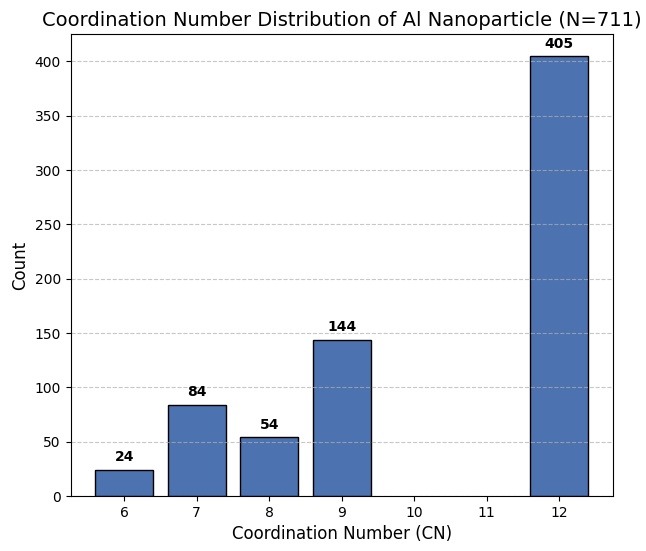
図4. 構築されたAlナノ粒子に対する配位数の解析結果。
4. 考察:理論モデルと実環境における挙動の違い#
Wulff法による予測は「熱力学的平衡状態」を示していますが、実際の材料開発では以下の要因も考慮する必要があります。本シミュレーション結果を「理想的な参照モデル」として、実験結果との差異を議論することが重要です。
- 温度効果(ラフニング): 融点に近い高温域では、エッジやコーナーの原子が熱揺らぎによって動きやすくなり、ファセットの角が取れて球形に近づく「ラフニング転移」が起こります。
- 非平衡成長(デンドライト): 急冷凝固など、成長速度が非常に速い場合は、表面エネルギーの安定性よりも熱や溶質の拡散速度が支配的となり、角の部分が優先的に成長して「樹枝状結晶(デンドライト)」となることがあります。
- 酸化被膜の影響: Alは非常に酸化しやすい金属です。酸素が存在する環境下では表面に酸化被膜が形成され、表面エネルギーのバランスが変化するため、真空中とは異なる形状を示す可能性があります。
まとめ#
本解析では、第一原理計算ソフトウェアAdvance/PHASEによって得られた高精度な表面エネルギー値を用い、Al結晶の平衡形状を予測しました。その結果、(111)面を主体とする切頂八面体形状が得られ、対応するナノ粒子モデルの構築や触媒活性点の解析もできることを示しました。第一原理計算とWulff法を組み合わせることで、様々な金属や化合物について、その安定形状を理論的に予測し、材料設計に活かすことが可能です。
本解析の詳細や、研究への適用可能性に関するご相談はこちら
お問い合わせ参考文献#
- R. L. Dobrushin, R. Kotecký, and S. B. Shlosman, Wulff construction: a global shape from local interaction, Translations of Mathematical Monographs, Vol. 104, American Mathematical Society (1992).
- 第一原理計算によるAl表面エネルギーの評価
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. Chevrier, K. A. Persson, and G. Ceder, "Python Materials Genomics (pymatgen) : A Robust, Open-Source Python Library for Materials Analysis", Comp. Mater. Sci. 68, 314 (2013).
- K. Mathew, A. K. Singh, J. J. Gabriel, K. Choudhary, S. B. Sinnott, A. V. Davydov, F. Tavazza, R. G. Hennig, "MPInterfaces: A Materials Project based Python tool for high-throughput computational screening of interfacial systems", Comp. Mater. Sci. 122, 183 (2016).
関連ページ#
- 第一原理計算ソフトウェア Advance/PHASE
- 解析分野:ナノ・バイオ
- 産業分野:材料・化学