DFT計算とマクロモデルの連携によるLiCoPO4正極の急速充電・破壊リスク解析#

高電圧正極材料オリビン型LiCoPO4(LCP)は、4.8 Vの高い作動電圧とオリビン構造由来の安全性を両立する材料として、次世代の高エネルギー密度バッテリーへの適用が検討されています。 しかし、高価なコバルトを使用する点に加え、 実用化の大きな技術的障壁となっているのが「急速充電時の寿命劣化」です。本解析事例では、第一原理計算ソフトウェアAdvance/PHASEを用いたDFT計算で得られた物性値をマルチフィジックス・モデル(SPM)へ連携させ、特にリスクが高いとされる急速充電(Fast Charging)時における、「電圧挙動」「発熱」および「粒子破壊リスク(引張応力)」を定量的に評価しました。なお、本結果はモデル仮定に基づくシナリオ解析の一例です。
Keywords: 第一原理計算(DFT), マルチスケール解析, リチウムイオン電池, LiCoPO4, 拡散係数, 活性化エネルギー, 単粒子モデル, 拡散誘起応力
解析手法と連携の指針#
1. 原子スケール:DFTによる物性算出#
シミュレーションの基盤となる材料固有の物性値をDFT+U計算により導出しました [1]。
- 活性化エネルギー (): NEB法により、Liイオンが安定サイト間を移動する際の障壁を 0.21 eV と算出しました。
- 開回路電圧 (OCV): 異なるLi濃度におけるエネルギー差に基づき、4.8V付近の平坦な電圧プロファイルを定義しました。
- 部分モル体積 (): 充放電に伴う格子定数変化から、体積膨張係数を決定しました。
2. スケール間連携#
DFTで得られた微視的パラメータを、以下の物理モデルを用いて巨視的パラメータへ変換しました。
拡散係数の温度依存性(アレニウスの式):
Liイオンの拡散挙動において、拡散係数の温度依存性を決定する活性化エネルギーにはDFT計算値 を採用しました。一方、頻度因子 については、ナノ構造化処理を施した高性能電極の実験的知見を参照し、キャリブレーションを行いました。時間ステップの選定にあたっては、数値計算の安定性を確保するため、von Neumannの安定性条件 [2] を考慮し、解析の収束性と計算効率の最適化を図っています。
3. マクロスケール:単粒子モデル (SPM) と粒径の影響#
活物質粒子内のLi濃度の空間・時間分布 と、それに伴う応力を以下の支配方程式で記述します [3]。ここで、粒径 は境界条件(フラックス)を通じて直接的に系に影響を与えます。
平衡状態のLiCoPO4は二相共存反応を示しますが、同型構造を持つLiFePO4に関する近年の研究 [4] では、高レート(急速充放電)下において非平衡な固溶体経路(Solid Solution Pathway)が支配的になることが示唆されています。本解析では、LiCoPO4においても同様の現象が生じると仮定し、Fickの法則に基づく単相拡散モデルを採用しています。この仮定の下で、急速充電時の挙動を予測します。
① 支配方程式(拡散方程式):
② 境界条件(粒径 の反映):
下記の式で示すように、粒子表面 () におけるリチウムのフラックス は、電流密度 (活物質重量あたり)と粒径 に依存します。粒径が大きいほど、同じ電流密度でも表面への負荷が集中します。Fはファラデー定数を表します。
③ 劣化指標(表面接線応力):
濃度勾配(平均濃度 と表面濃度 の差)に起因して発生する応力です [5]。
充電(脱離)時は表面濃度が低下するため となり、表面接線応力は正の値(引張)を示します。
計算条件#
Pythonスクリプトによる数値解析に用いた主なパラメータを表1に示します。ヤング率については、一般的な酸化物セラミックスの値を参照し150GPaと設定しました。
表1. マルチスケール解析の入力パラメーター
| カテゴリー | パラメーター | 値 | 単位 |
|---|---|---|---|
| DFT計算由来 | 活性化エネルギー () | 0.21 | eV |
| 開回路電圧 (OCV) | DFTプロファイル | V | |
| 部分モル体積 () | 2.0 × 10-6 | m3/mol | |
| 活物質物性 | 頻度因子 () | 8.0 × 10-14 | m2/s |
| 理論容量 | 167 | mAh/g | |
| 機械的特性 | ヤング率 () | 150 | GPa |
| ポアソン比 () | 0.3 | - | |
| 計算条件 | Cレート | 1C, 5C | - |
| 粒子半径 () | 50 - 500 | nm |
解析結果と考察#
以下に、粒子半径 のモデルに対し、通常充電(1C)と急速充電(5C)を行った際のシミュレーション結果を示し、それぞれの物理現象について考察します。
充電電圧挙動と過電圧の影響#
図1は、定電流充電を行った際の電圧プロファイルの比較です。1C充電(青線)では、材料固有のOCVに近い緩やかな電圧上昇が見られます。一方、5C急速充電(橙線)では、充電開始直後に電圧が急激に立ち上がっています。これは、大電流によるオーミック抵抗および拡散遅れに伴う濃度分極(過電圧)が顕著に現れた結果です。この過電圧により、粒子の内部はまだリチウムで満たされているにもかかわらず、表面電圧のみが上限カットオフ電圧(5.2V)に到達してしまい、充電プロセスが極めて短時間で強制終了されていることが分かります。本解析では5.2Vまでの電圧上昇が見られますが、一般的な電解液の酸化分解電位(約4.5V)を超過しています。この結果は、「現状の活物質粒子設計のままでは、電解液の分解を招くほどの過電圧が生じる」というリスクを示唆するものです。実用化には、後述する粒径制御による過電圧低減や、高耐圧電解液の併用が必須となります。
なお、本解析は活物質単体に焦点を当てた単粒子モデル(SPM)であるため、上記の結果は「固体内拡散」に起因する過電圧を示しています。実際の多孔質電極を用いたセルにおいては、5Cのような高レート下では電解液中のイオン枯渇(液相拡散律速)が支配的要因となり、本解析結果よりもさらに早期に電圧カットオフに到達する可能性があります。したがって、本結果は活物質の性能限界を示したものであり、セル設計時には電極厚みや空隙率の最適化が別途必要となります。
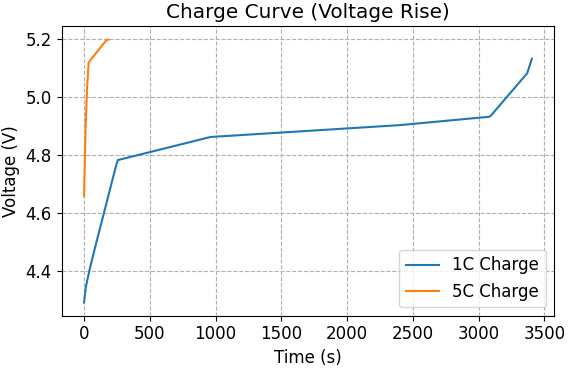
図1. 充電曲線の比較 (1C vs 5C)。5C充電では過電圧により実効容量が大幅に制限されます。
発熱速度と熱暴走リスク#
図2に、充電中の発熱速度(W/g)の推移を示します。1C充電では発熱は低く一定に保たれていますが、5C充電時には、通電開始直後(t≒0)に 0.5 W/g を超える急激な発熱ピークが観測されました。これは、静止状態から急激に大電流(5C)を流した際に生じる、オーミック抵抗および活性化過電圧の瞬間的な立ち上がりに起因するものです。この初期発熱は、セル内の温度分布に不均一をもたらすトリガーとなるため注意が必要です。
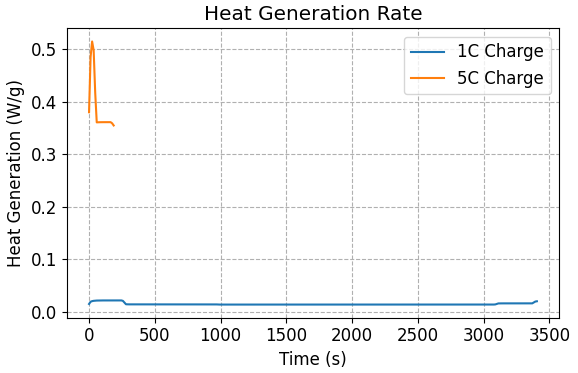
図2. 発熱速度の推移。急速充電初期に極めて高い熱エネルギーが発生しています。
粒子破壊のメカニズム(引張応力)#
充電時、粒子表面からはリチウムが脱離して結晶格子が収縮しようとしますが、リチウムが残存している中心部は膨張したままの状態を保ちます。この体積差により、粒子表面には常に引張方向(引き裂かれる方向)の応力、すなわち引張応力(Tensile Stress)が生じます(図3a)。図3bに、本解析の主要な着眼点である「拡散誘起応力(Diffusion Induced Stress)」の推移を示します。
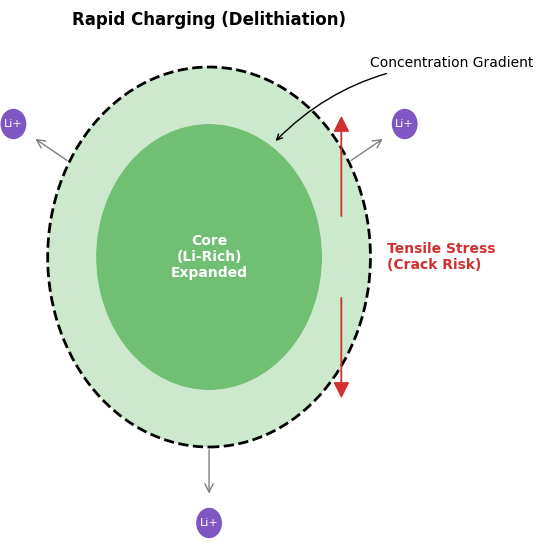
図3a. 急速充電時の濃度勾配と表面引張応力の発生メカニズム
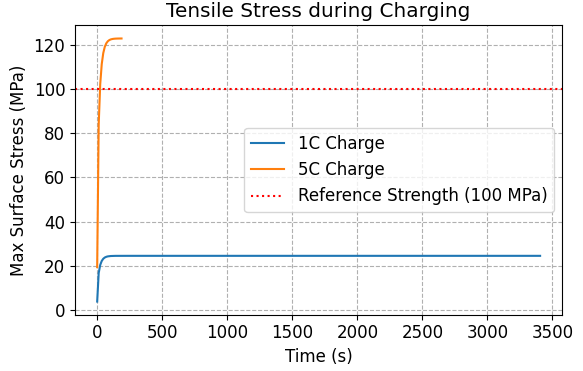
図3b. 充電中の最大表面応力の推移。5C充電では、セラミックス材料の一般的な破壊リスク領域(参考値 100MPa)を超える大きな応力が予測されます。
考察:応力値に基づく破壊リスク評価
解析の結果、5C急速充電時には最大で 120 MPa を超える引張応力が発生すると予測されました。Woodfordら [6] が指摘するように、脆性材料の実際の破壊は応力値のみでは決定されず、材料の破壊靭性()と内在する欠陥サイズ(flaw size)の関係(破壊力学)に依存します。しかしながら、120 MPaという値は一般的な酸化物セラミックスの強度分布の下限付近に位置するため、製造上の欠陥(マイクロクラック等)が存在する場合、破壊が進展するリスクが高い領域にあると解釈するのが妥当です。
感度解析による粒径設計#
上述の「容量低下」と「粒子破壊」の課題を同時に解決するための設計解を探索するため、粒子径を設計変数とした感度解析を行いました。
容量確保のための粒径設計#
図4は、粒子半径と充電容量(SOC利用率)の関係を示しています。5C充電(橙線)において、粒子半径が100 nmを超えると、利用可能な容量は30%以下にまで急減します。これは、粒子が大きくなるほどリチウムの拡散距離が長くなり、中心部まで反応が進む前に表面電圧が上限に達するためです。実用的な容量(例えば80%以上)を確保するためには、粒子径を大幅に微細化する必要があります。
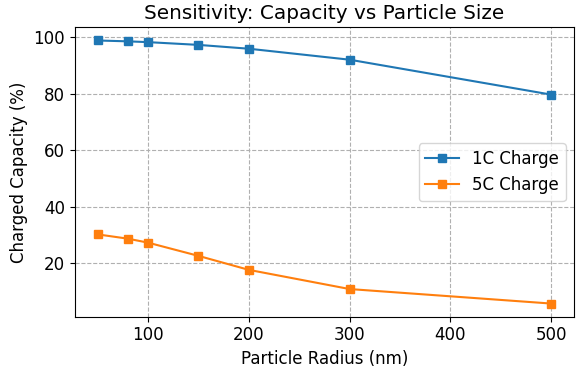
図4. 粒子径と充電容量の関係。
破壊回避のための粒径設計#
図5は、粒子半径と最大引張応力の関係を示しています。粒子径が大きくなるにつれて応力は単調増加しますが、注目すべきは強度下限(100 MPa)との交点です。5Cという過酷な充電レート下において、応力をこの強度目安以下に抑制するためには、粒子半径を 80 nm 以下に制御することが推奨されます。
Woodfordらによる理論解析 [6] では、他の正極材料における破壊臨界粒径も報告されています。例えば、格子体積変化が比較的穏やかな層状岩塩型 LiCoO2 では約 420 nm と大きめですが、充放電に伴う激しい相変態(立方晶⇔正方晶)により大きな異方性ひずみが生じるスピネル型 LiMn2O4 では約 11 nm と極めて微細な粒子設計が要求されます。本解析で導出された LiCoPO4 の 80 nm という値は、これらの中間のオーダーに位置しています。これは、オリビン型構造がLiCoO2よりも高い剛性を持つ一方で、LiMn2O4ほど急激な相変態は生じないという物理的特性を反映した、整合的な結果であると考えられます。
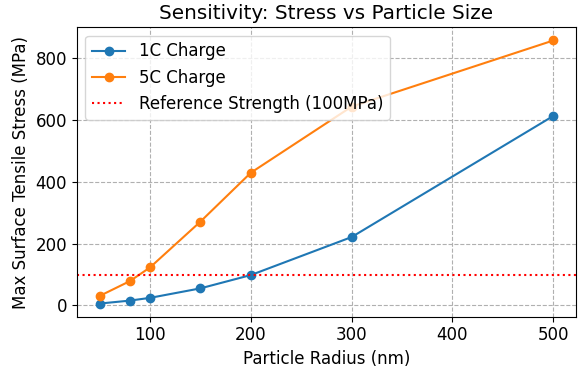
図5. 粒子径と最大引張応力の関係。微粒子化による応力低減効果が確認されています。
実用化に向けた課題:化学的安定性とのトレードオフ
本解析により、機械的破壊を防ぐための幾何学的目安()が導かれました。一方、高電圧(約4.8V vs Li/Li+)で作動するLiCoPO4において、粒子をナノ化して比表面積を増大させることは、電解液との界面副反応(酸化分解)を加速させる要因となります。
したがって、粒子半径 80 nm(直径換算で 160 nm)以下の微粒子を採用する際は、単なるサイズ制御だけでなく、電解液との直接接触を防ぐための表面コーティング技術(カーボンコートや酸化物被覆等)や、高電位安定性電解液の選定といった、化学的劣化(容量低下)を抑制する対策との併用が設計上の要件となります。
まとめ#
本解析では、第一原理計算ソフトウェアAdvance/PHASEを用いたDFT計算により導出したLiCoPO4の固有物性をマクロモデルへと連携させ、正極における急速充電時の挙動を評価しました。シミュレーションの結果、5Cのような高レート充電下では固体内拡散の遅れが支配的要因となり、容量の大幅な低下とともに、粒子表面に高い引張応力(120 MPa超)が発生する可能性が示されました。感度解析の結果から、粒子径をナノサイズ(例:半径80nm以下)に制御することは、拡散律速による容量低下を回避し、かつ拡散誘起応力を低減させて機械的信頼性を向上させるための合理的な設計指針であると考えられます。
本解析の詳細や、研究への適用可能性に関するご相談はこちら
お問い合わせ参考文献#
- Advance/PHASEによるリチウムイオン二次電池正極材料の解析: 起電力・イオン伝導性
- 安部公輔, 東森信就, 久保雅義, 藤原宏志, 磯祐介, "Courant-Friedrichs-Lewy 条件についての注意 (理論)", 日本応用数理学会論文誌 24, 15 (2014).
- M. Doyle, T. F. Fuller, and J. Newman, "Modeling of Galvanostatic Charge and Discharge of the Lithium/Polymer/Insertion Cell", J. Electrochem. Soc. 140, 1526 (1993).
- R. Malik, F. Zhou, and G. Ceder, "Kinetics of non-equilibrium lithium incorporation in LiFePO4", Nat. Mater. 10, 587 (2011).
- X. Zhang, W. Shyy, and A. M. Sastry, "Numerical Simulation of Intercalation-Induced Stress in Li-Ion Battery Electrode Particles", J. Electrochem. Soc. 154, A910 (2007).
- W. H. Woodford, W. C. Carter, and Y.-M. Chiang, "Design criteria for electrochemical shock resistant battery electrodes", Energy Environ. Sci. 5, 8014 (2012).
関連ページ#
- 第一原理計算ソフトウェア Advance/PHASE
- 解析分野:ナノ・バイオ
- 産業分野:材料・化学