Advance/PHASEによるリチウムイオン二次電池正極材料の解析#

リチウムイオン二次電池の性能は正極材料に大きく依存するため、新規材料の開発が重要な課題です。実験では困難な原子レベルの挙動を予測できる第一原理シミュレーションは、この開発を加速させる強力なツールとなります。本稿では、第一原理計算ソフトウェアAdvance/PHASEを用い、高電圧正極のモデル材料として研究されるオリビン型LiCoPO₄の重要特性（起電力、イオン伝導性）を解析した事例を紹介します。

Keywords: First-principles calculation, Rechargeable Li-ion Battery, Olivine-type LiCoPO4

オリビン型リチウムイオン電池正極材料#

大容量のリチウムイオン電池を安価に作成するためには、新たな電極材料の開発が活発に進められています [1]。ここでは、リチウムイオン電池正極材料の例としてLiCoPO₄を取り上げます。その結晶構造を、全てのリチウムイオンが離脱した構造（CoPO₄）とともに図1に示します。

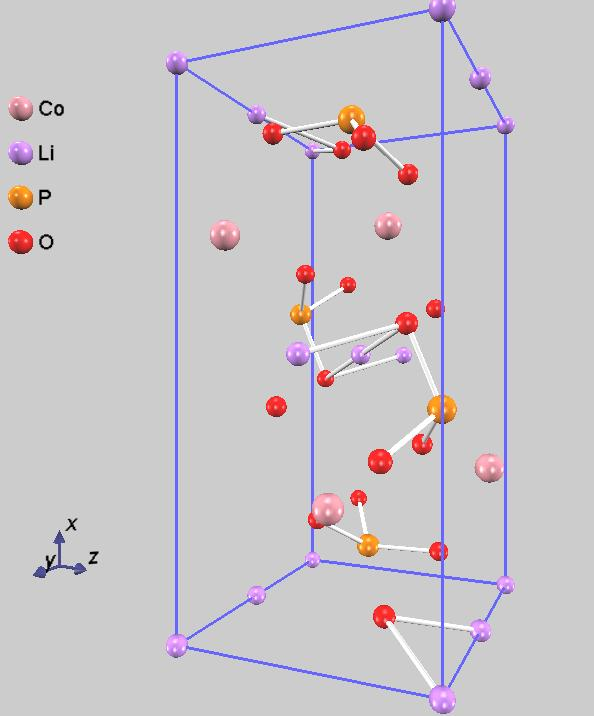
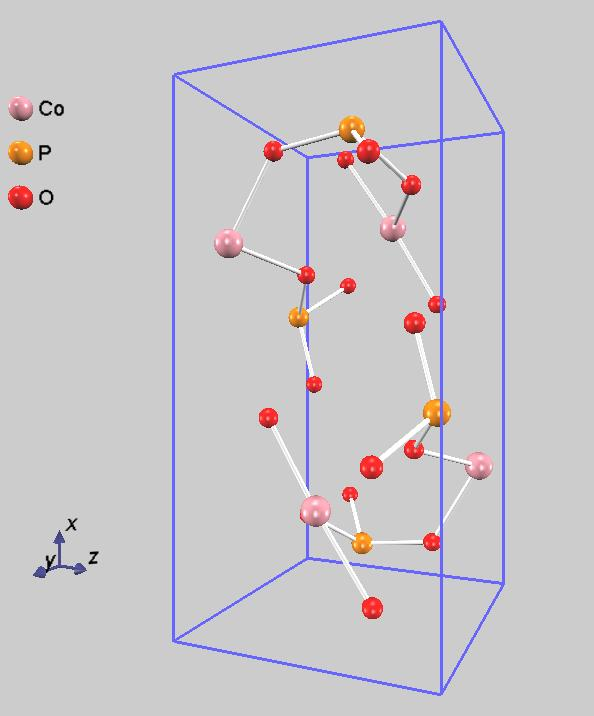
図1． LiCoPO₄ （左）とCoPO₄（右）の結晶構造。格子境界面上の原子を重複して表示しています。

この構造はオリビン型と呼ばれ、熱安定性に優れていることが特徴です。ところで、このオリビン構造で高価なコバルトを、より安価で資源豊富な鉄 (Fe) に置換したLiFePO₄（LFP）は、安全性・長寿命・低コストを兼ね備えた正極材料として、現在広く実用化されています。さらに近年では、LFPの作動電圧をさらに引き上げるため、マンガン(Mn)などを加えたLMFP（リン酸マンガン鉄リチウム）などが、次世代のコバルトフリー材料として活発に開発されています。遷移金属種に関係なく、いずれの元素であっても解析の手順は同じであるので、ここでは高電圧正極材料として知られるLiCoPO₄を対象として解説します。

計算手法#

計算には密度汎関数法（DFT）を用いました。LiCoPO₄は遷移金属酸化物であり、そのCo 3d電子は局在性が強いです。一般的なGGA近似では、このような局在電子間の強いクーロン相互作用を正しく記述できないため、これを補正するDFT+U法を適用しました [2]。計算に用いたUパラメータは文献 [3] の値を採用し、その値を表1に示します。

表1．パラメータUの値（単位：eV）

	LiCoPO₄	CoPO₄
U	5.05	6.34

また、計算に用いた主な計算条件は、表2にまとめています。

表2．主な計算条件

汎関数	GGA(PBE)+U
カットオフエネルギー	波動関数	25.0 Rydberg
カットオフエネルギー	電荷密度	230.0 Rydberg
k点分割数	単位格子	1×2×2
k点分割数	スーパーセル	1×2×1
電子状態（エネルギー）収束条件	10^-8 Hartree/Atom

計算結果#

安定な格子定数#

すでに述べたように、リチウムイオン電池正極では、充放電にともなってリチウムイオンの離脱・挿入が起こり、その際には体積変化が生じます。大きな体積変化は、二次電池の充放電サイクルにおける電池の形状変化につながるため好ましくありません。実用化されているリチウムイオン二次電池では、体積変化の少ない材料が選ばれており、オリビン型の材料でも大きな変化はありません。しかしながら精密な解析のためには、この体積変化によるエネルギー変化をも考慮する必要があると考え、本解析でもその影響を取り入れました。

表3．安定な格子定数（単位：Å）

	LiCoPO₄		CoPO₄
	計算	実験	計算	実験
a	10.49	10.20	10.16	10.09
b	6.05	5.92	5.88	5.85
c	4.82	4.70	4.84	4.72

DFT+U計算で求めた安定な格子定数を表3に示します。また、表3には実験値 [4] も併記しました。計算結果は、実験値を良く再現しています。一般に、密度汎関数法（GGA）の計算では、格子定数は実験値と比較してわずかに大きくなることが知られており、ここでもその傾向がみられます。また、LiCoPO₄とCoPO₄の格子定数計算結果を比較すると、a, b軸についてはLiCoPO₄の方が長いですが、c軸はCoPO₄の方が長いという点についても、実験結果を再現しています。

起電力#

電池の起電力（電圧）は、正極材料と負極材料との間のエネルギー差で決まります。正極材料の評価では、負極として慣例的に金属リチウムを基準とし、リチウムイオン1つが移動する際のエネルギー変化を式(1)で算出します。

$V = \dfrac{E(\text{Li}_x\text{CoPO}_4) - \delta E(\text{Li}) - E(\text{Li}_{x-\delta}\text{CoPO}_4)}{e\delta} \quad (1)$

ここで、 $E_{\text{Li}_x\text{CoPO}_4}$ はLi_xCoPO₄のエネルギー、 $E_{\text{Li}}$ は金属リチウム1原子当たりのエネルギー、 $e$ は素電荷です。第一原理計算は有限サイズのセルで計算するため、リチウム濃度 $x$ は離散的な値を取ります。例えば単位格子中のLiが4つなら、 $x$ の刻み幅は0.25です。より細かい濃度ステップを再現するには、単位格子を複数並べたスーパーセルを用います。ただし、セルサイズが異なる計算のエネルギーを比較するには、計算条件の整合性を取る必要があります。特に重要なのがk点サンプリングで、セルをある方向に2倍に拡げると、対応する逆格子空間（ブリルアンゾーン）は半分に縮小します。そのため、k点分割数も半分にすることで、物理的に等価なサンプリングとなり、エネルギーの比較が可能になります。

今回の計算では、Li濃度に応じて単位格子とスーパーセルを使い分け、エネルギーを算出しました（表4）。計算コストを考慮し、格子定数の最適化は中間濃度である $x=0.5$ の場合のみ実施しました。Uの大きさは、 $0 \le x < 0.5$ の範囲ではCoPO₄に用いた値、 $0.5 < x \le 1$ の範囲ではLiCoPO₄に用いた値と同じ値をそれぞれ使用し、 $x=0.5$ の場合のみ両者の平均値を用いました。得られたエネルギーから電圧を評価する際には、2つの方法を用いました。一つは、フル充電からフル放電（ $\Delta x = 1$ ）させた際の「平均電圧」です。もう一つは、各濃度ステップ（最小 $\Delta x$ ）における「局所的な電圧」です。表4にまとめた通り、これらの計算結果は実験値である4.8V [4] と良い一致を示しました。

表4．Li_xCoPO₄ (0 ≤ x ≤ 1)のエネルギー（単位：Hartree）と起電力（単位：V）

x	1.0	0.875	0.75	0.5	0.25	0.125	0.0
x	LiCoPO₄	2LiCoPO₄-Li	LiCoPO₄-Li	CoPO₄+2Li	CoPO₄+Li	2CoPO₄+Li	CoPO₄
スーパーセルのエネルギー (2格子分)	-807.94257	-807.51928	-807.10790	-806.15066	-805.18843	-804.78028	-804.36538
単位格子のエネルギー	-403.97129		-403.55395	-403.07533	-402.59422		-402.18269
リチウム数 (2格子分)	8	7	6	4	2	1	0
起電力 (δ=0.125)	4.36	4.04	5.87	5.93	3.95	4.13
起電力 (δ=x)	5.01	5.10	5.28	4.99	4.04	4.13
格子定数	LiCoPO₄の格子定数を使用			最適化※	CoPO₄の格子定数を使用

最後に、本解析の限界とシミュレーションにおける判断の重要性について述べます。今回の計算では、各濃度で一通りのリチウム配置のみを考慮しました。より現実に近いシミュレーションを行うには、考えられる様々なリチウム配置を試し、都度格子定数を最適化することが理想です。しかし、それらを全て行うと計算規模は膨大になります。したがって、どの物理現象が本質的に重要かを見極め、計算可能な範囲にモデルを簡略化する研究者の判断が、第一原理シミュレーションを有効に活用する上で極めて重要となります。

遷移状態探索#

二次電池の充放電速度（レート特性）は、電極材料内部でのリチウムイオンの移動しやすさ、すなわちイオン伝導度に大きく依存します。この「移動しやすさ」を定量的に評価するためには、リチウムイオンが結晶格子内のある安定サイトから別の安定サイトへ移動する際の活性化エネルギー（ $E_a$ ）を求めることが重要です。活性化エネルギーが低いほど、イオンは移動しやすくなります。ここでは、この活性化エネルギーをnudged elastic band (NEB)法を用いて算出しました。

始状態と終状態の設定#

NEB法による計算に先だって、始状態と終状態を求める必要があります。計算対象はCoPO₄にリチウムイオンが1つだけ挿入された系とし、構造最適化計算を行いました。始状態と終状態の違いは挿入したリチウムイオンが存在する位置です。本解析ではb軸方向へのリチウムイオン伝導を考えました [5]。始状態と終状態を図2に示しています。

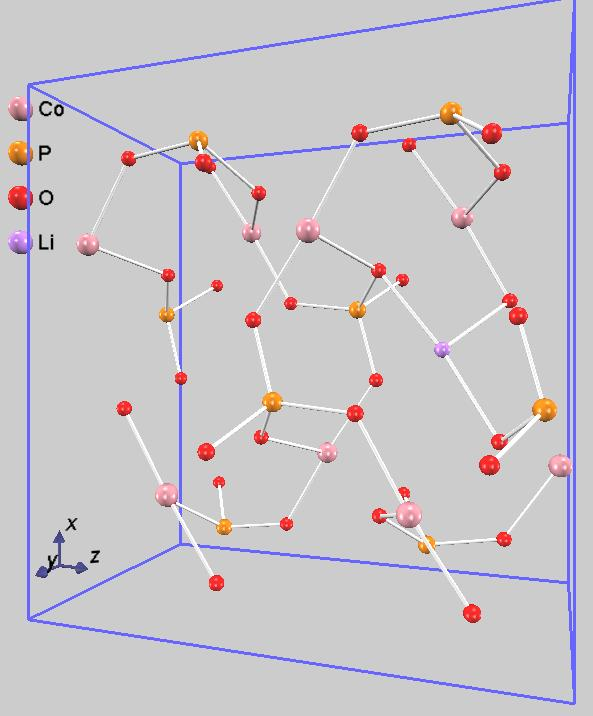
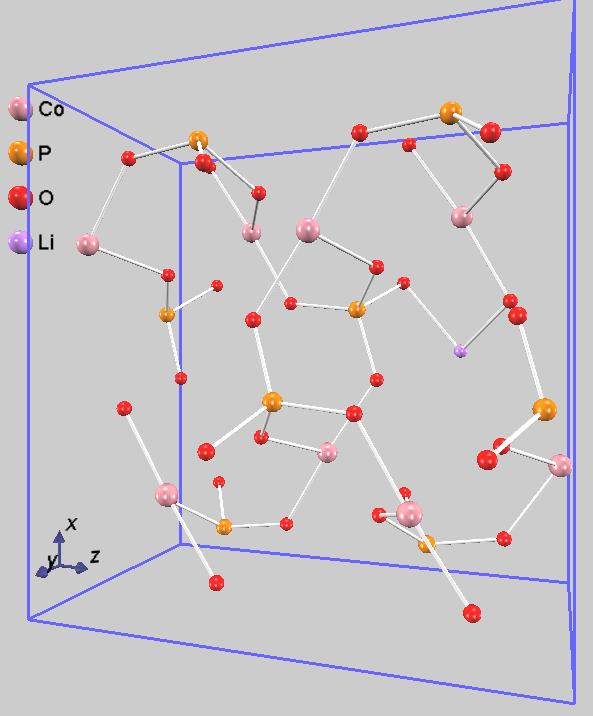
図2．リチウムイオン伝導の始状態（左）と終状態（右）

活性化エネルギーと反応経路#

上記で設定した始状態と終状態を用いてNEB計算を行い、反応経路に沿ったエネルギー変化を求めました。この計算では、始状態と終状態の間に7個の中間イメージを配置しました。得られたエネルギープロファイルを図3に示します。 (始状態を0, 終状態を1とするnormalized reaction coordinateを使用しています。) このプロファイルの頂点から、リチウムイオンが移動する際の活性化エネルギーは0.21 eVと算出されました。この値は、他のオリビン系正極材料と比較しても良好な値であり、既存の計算結果[6]とも良く一致しています。

図3．CoPO₄におけるリチウムイオンの移動に伴うエネルギー変化

また、遷移状態を含む伝導過程での原子配置を図4に示します。図4中央の遷移状態の構造を詳しく見ると、移動中のリチウムイオンは、周囲の酸素原子に最も接近していることがわかります。このLi-O原子間の反発、あるいはリチウムイオンが通過する「窓」の狭さが、エネルギー障壁の主な要因であると考えられます。リチウムイオンが始状態と終状態の間を直線で移動せず、わずかに迂回する経路（図では進行方向に向かって右下方向）を通っているのは、このエネルギー的に不利な相互作用を避けるためです。これは、NEB法によって物理的に最も妥当な最小エネルギー経路が特定されたことを示しています。

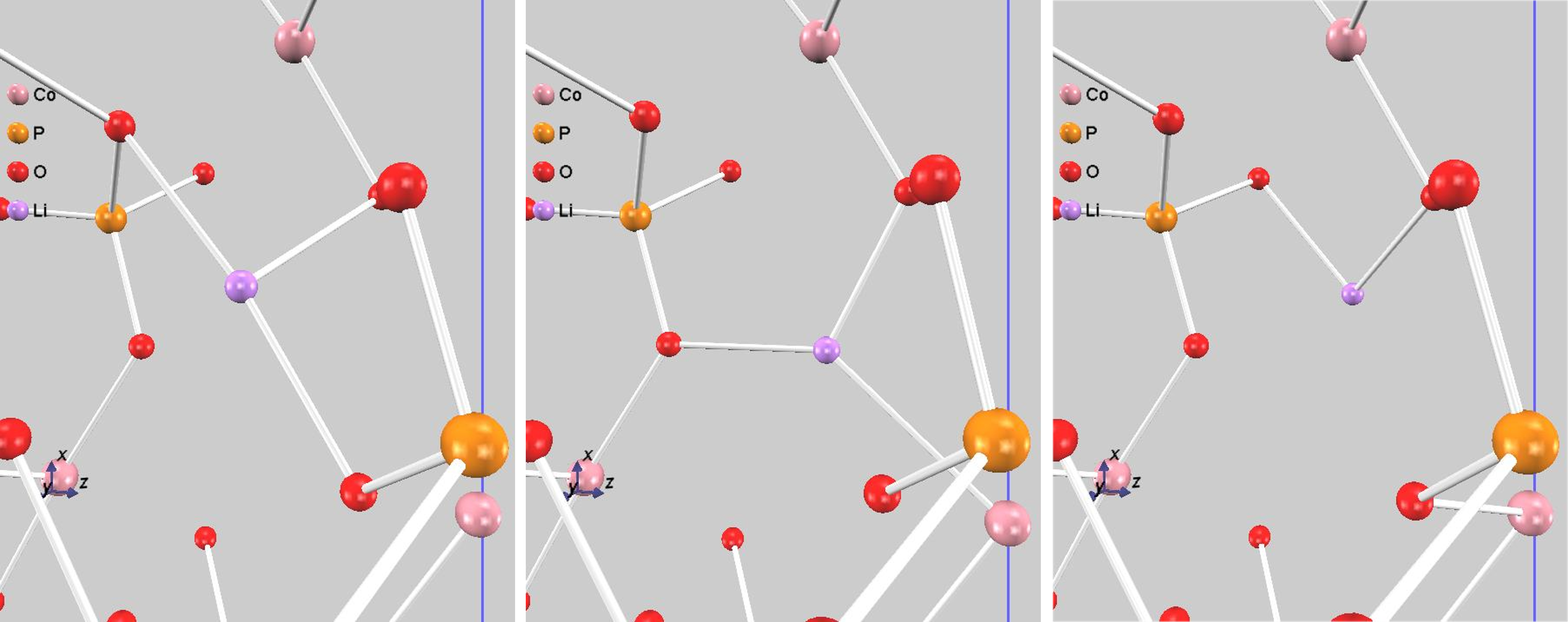
図4．リチウムイオン伝導過程：始状態（左）、遷移状態（中）終状態（右）

まとめ#

リチウムイオン二次電池正極材料としてLiCoPO₄の性質を調べました。安定な格子定数、起電力、リチウムイオン伝導障壁を求め、実験結果や既存の計算結果と良く一致する結果が得られました。本解析のように、原子レベルで精密に物事を解析するタイプの課題にとっては、第一原理シミュレーションが非常に強力なツールになり得ます。

参考文献#

芳尾真幸／小沢昭弥（編）：“リチウムイオン二次電池第二版　材料と応用”、日刊工業新聞社 (2000).
O. Le Bacq, A. Pasturel, and O. Bengone: “Impact on electronic correlations on the structural stability, magnetism, and voltage of LiCoPO4 battery”, Phys. Rev. B 69, 245107 (2004).
F. Zhou, M. Cococcioni, C. A. Marianetti, D. Morgan, and G. Ceder: “First-principles prediction of redox potentials in transition-metal compounds with LDA+U”, Phys. Rev. B 70, 235121 (2004).
K. Amine, H. Yasuda, and M. Yamachi: “Olivine LiCoPO4 as 4.8 V Electrode Material for Lithium Batteries”, Electrochem. Solid-State Lett. 3, 178 (2000).
D. Morgan, A. Van der Ven, and G. Ceder: “Li Conductivity in LixMPO4 (M = Mn, Fe, Co, Ni) Olivine Materials”, Electrochem. Solid-State Lett. 7, A30 (2004).
中山将伸、脇原將孝：“第一原理バンド計算によるリチウムイオン電池正極材料LiMPO4 (M = Mn, Fe, Co, Ni)のバルク特性の研究”，Electrochemistry 76, 752 (2008).