深層学習運動エネルギー汎関数AdvanceSoft25によるエネルギー-体積曲線と体積弾性率の計算#
材料物性予測のための密度汎関数理論(DFT)計算の解法として最も広く知られているKohn-Sham DFT (KS-DFT)では、計算コストが系のサイズに対してで増大することが課題でした。 これを解決する手法として提案されたOrbital-Free DFT (OF-DFT)では、計算コストがでスケールし、大きなサイズの系に対しても高速な計算を実現します。
一方で、OF-DFTでは実用に耐えうる精度の運動エネルギー汎関数が未知であることが課題でした。 そこで、アドバンスソフト株式会社では、独自の場の深層化アルゴリズムを適用した深層学習運動エネルギー汎関数AdvanceSoft25 (AS25)を開発し、Advance/OF-DFTに搭載しました。 AS25は、OF-DFTの最大のメリットであるの計算コストを維持しながら、従来の運動エネルギー汎関数よりも高精度な電子密度計算を実現しました。
本記事では、AS25の応用事例として、以下の計算を行いました
- 従来の運動エネルギー汎関数とAS25のエネルギー-体積曲線の比較
- AS25によるエネルギー-体積曲線と体積弾性率の計算
計算条件#
従来の運動エネルギー汎関数とAS25のエネルギー-体積曲線の比較#
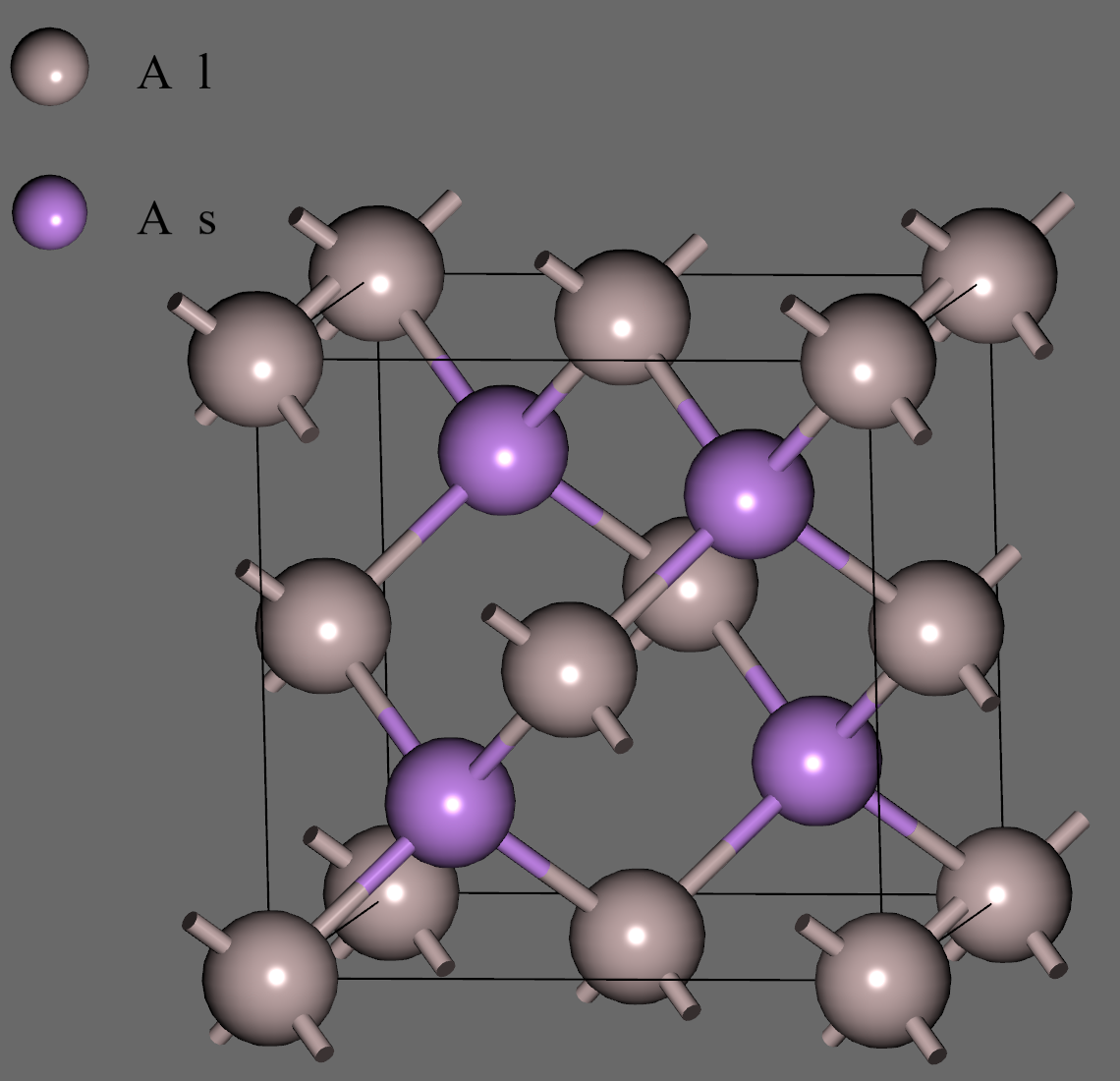
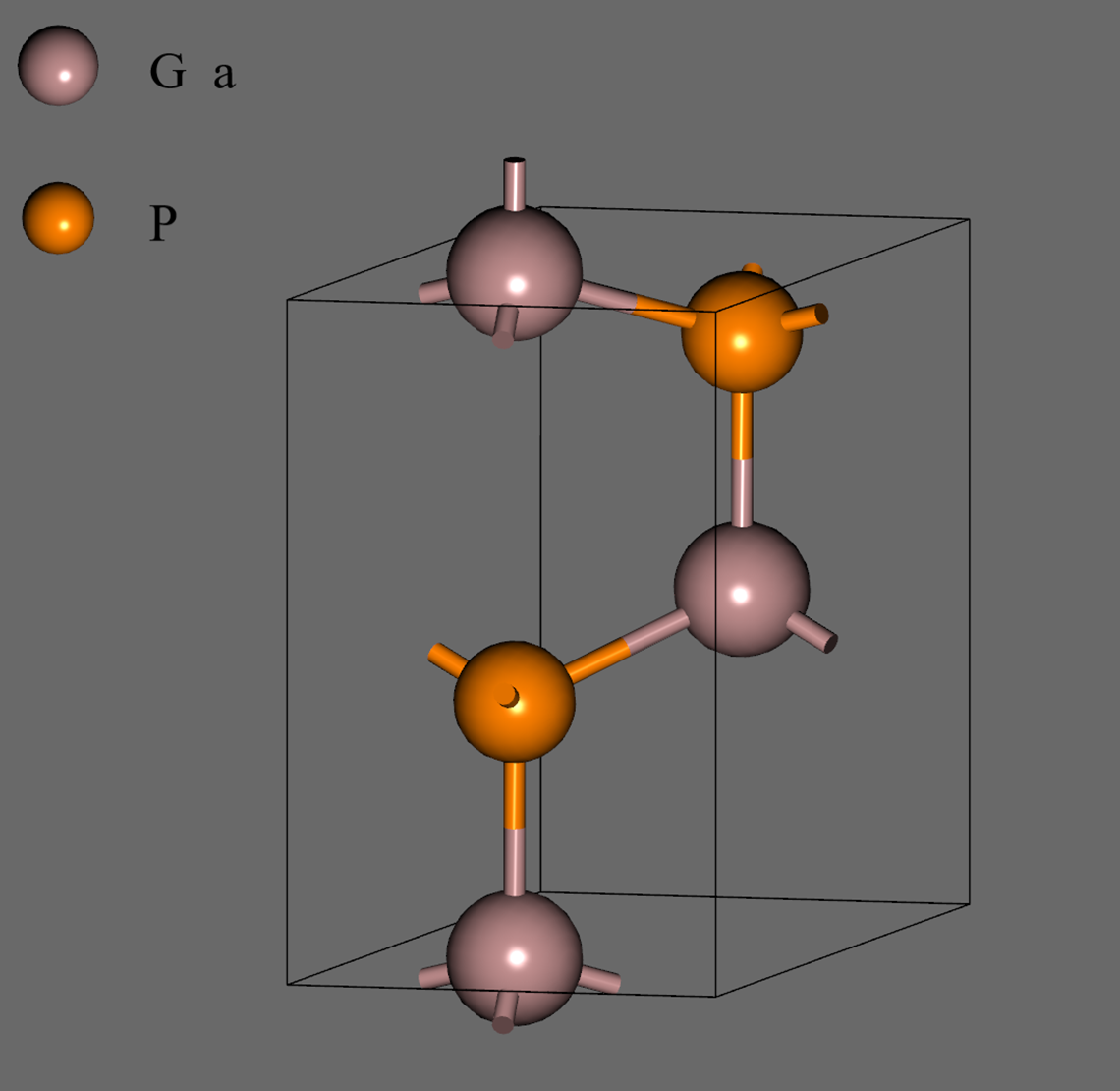
従来の運動エネルギー(KE)汎関数との比較に使用する構造として、典型的な半導体材料であるZinc-blende構造のAlAs (mp-2172)とWurtzite構造のGaP (mp-8882)をMaterials Projectより取得して使用しました。
以下の計算条件の下で、体積を変化させながらKS-DFT計算及びOF-DFT計算を実行しました。
- 波動関数のカットオフエネルギー : ~ 820 eV
- 擬ポテンシャル : OEPP
- 交換相関汎関数 : LDA
- k点サンプリング : ~ 0.04 Å-1
KS-DFTにはQuantum ESPRESSO 6.7 (アドバンスソフト改修版)を使用しました。 また、OF-DFTのKE汎関数としては、AS25に加えて、既存のよく知られているTFλvW、LKT、HC1を用いて計算を行いました。
|
|
| AlAs | GaP |
AS25によるエネルギー-体積曲線と体積弾性率の計算#
体積弾性率を計算するデータセットとして、Manzhosら2による先行研究で使用している約400構造3を、Materials Projectから取得して使用しました。
以下の計算条件の下で、体積を変化させながらKS-DFT計算及びOF-DFT計算を実行しました。
- 波動関数のカットオフエネルギー : 1250 eV
- 擬ポテンシャル : OEPP
- 交換相関汎関数 : LDA
- k点サンプリング : 0.05 Å-1
KS-DFTにはQuantum ESPRESSO 6.7 (アドバンスソフト改修版)を使用しました。 また、OF-DFTのKE汎関数としてはAS25を用いて計算を行いました。
計算結果#
従来の運動エネルギー汎関数とAS25のエネルギー-体積曲線の比較#
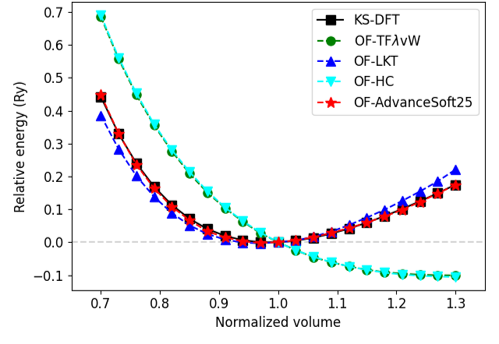
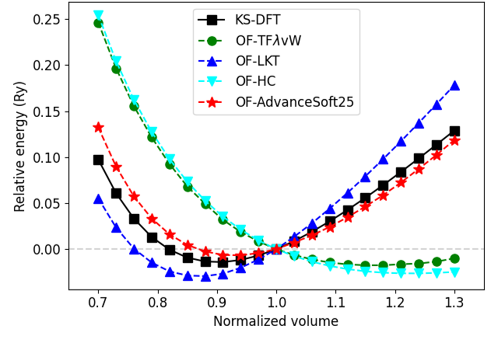
計算の結果として得られた各構造におけるエネルギー-体積曲線を以下の図に示します。 図中の横軸および縦軸は、それぞれ体積を変化させる前の構造を基準として規格化した体積、トータルエネルギーの相対値に対応します。
|
|
| AlAs | GaP |
上図からは、いずれの構造においても、AS25が最も精度よくKS-DFTのエネルギー-体積曲線を再現できていることがわかります。 一方、標準的な構造のベンチマークにおいては従来KE汎関数の中で最も高精度であったHCは、KS-DFTのエネルギー-体積曲線を全く再現できていません。 これは、精度がパラメータに強く依存し、構造ごとに最適化を行わなければならないHCの汎用性の低さを示していると考えられます。
AS25によるエネルギー-体積曲線と体積弾性率の計算#
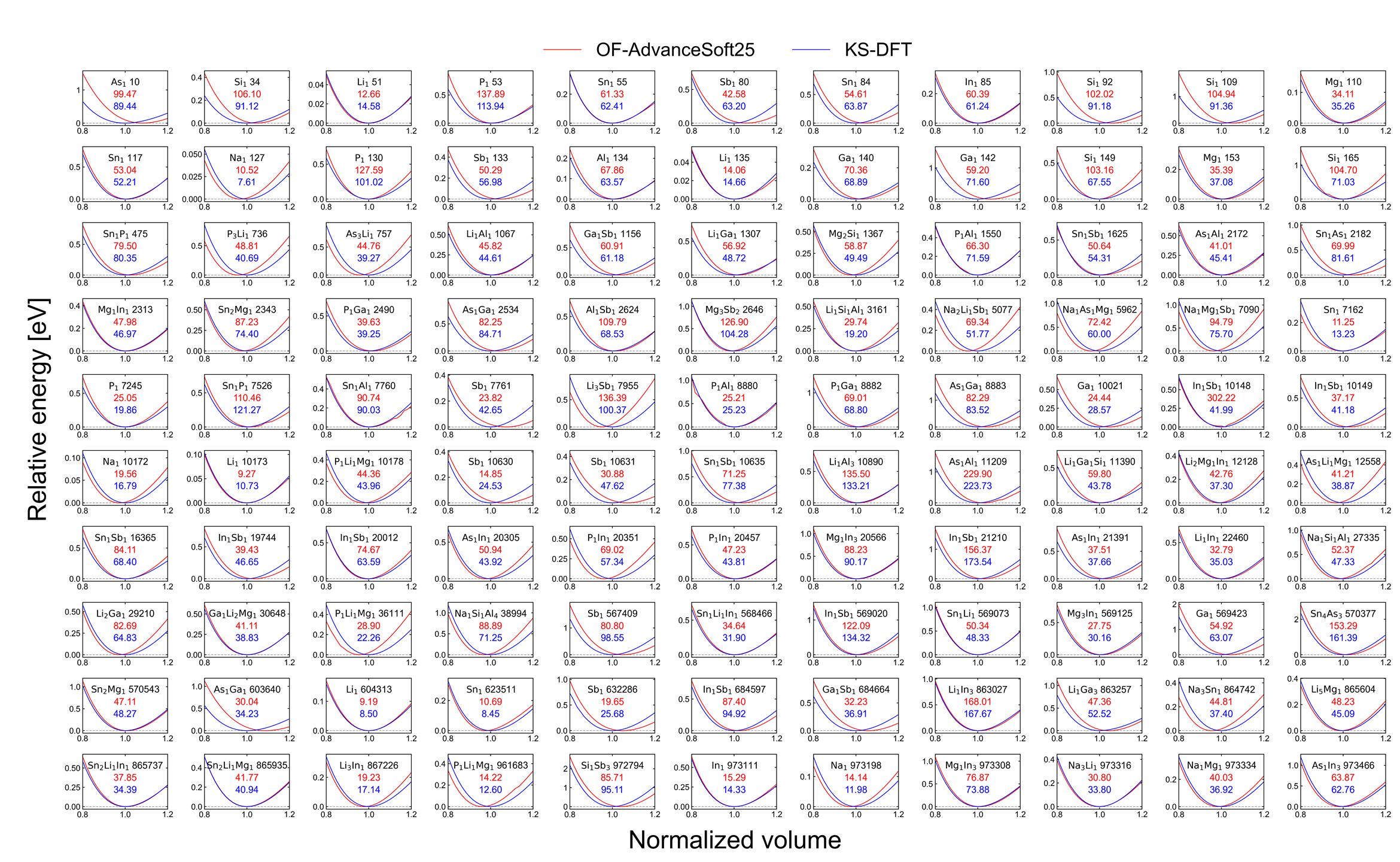
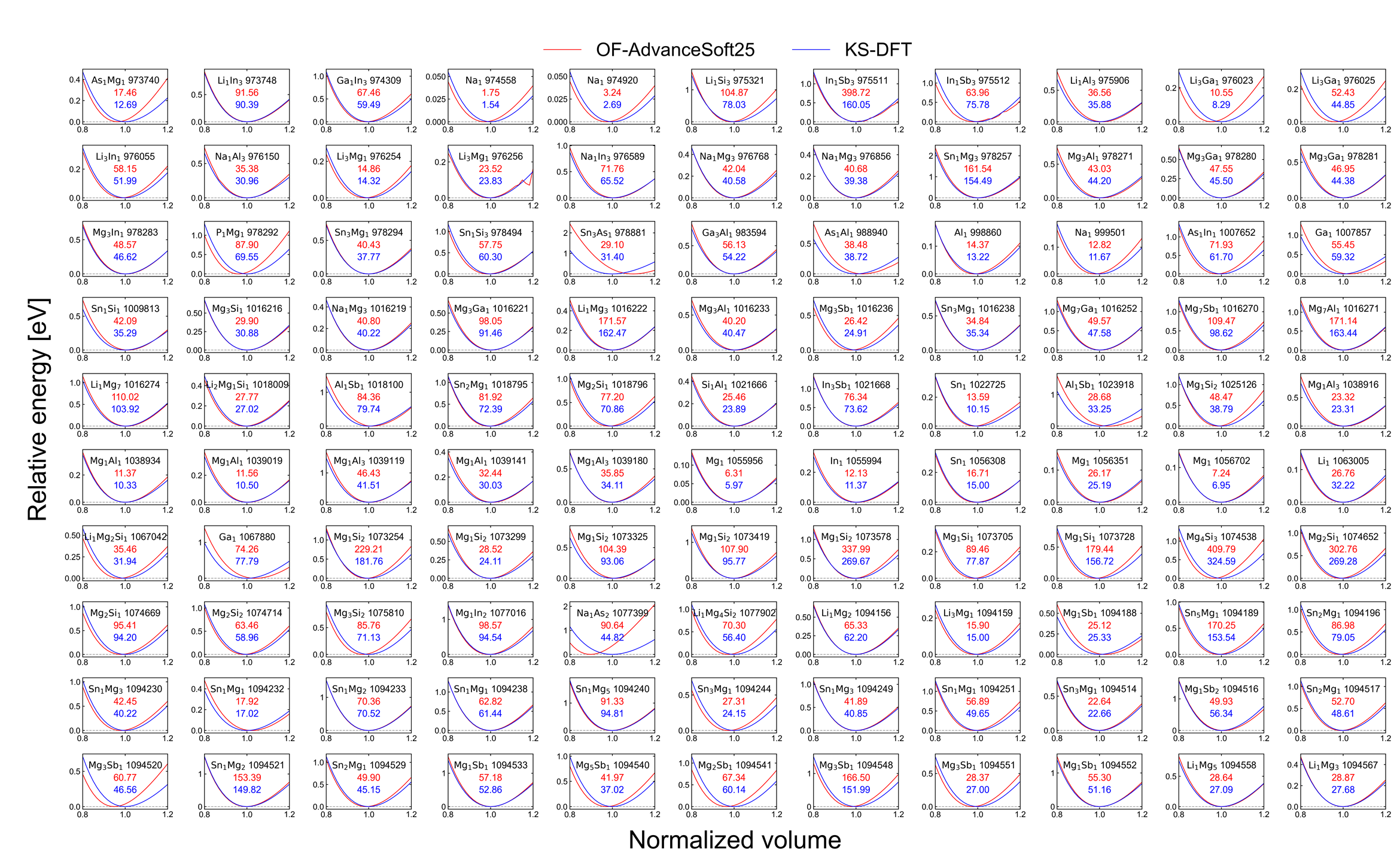
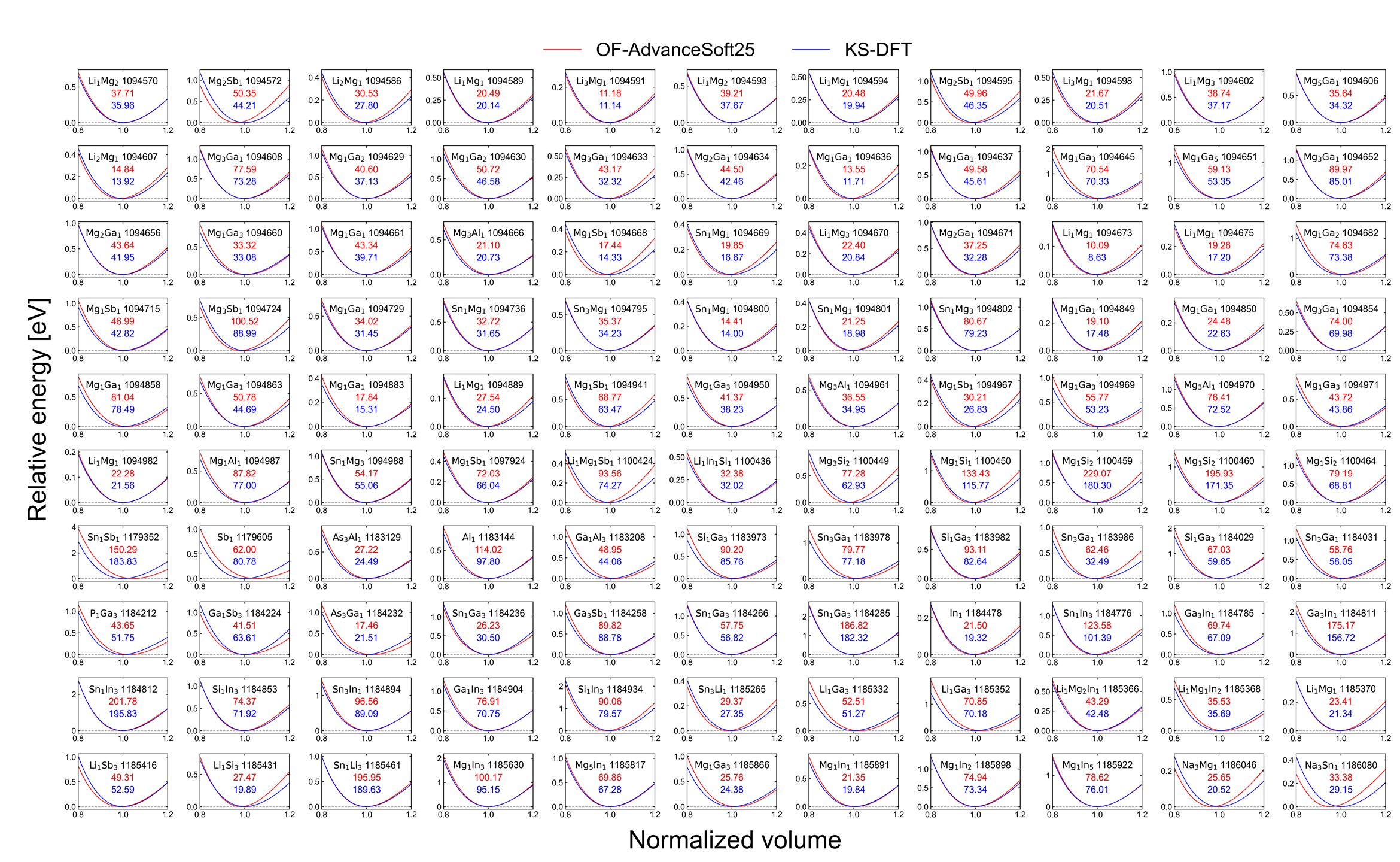
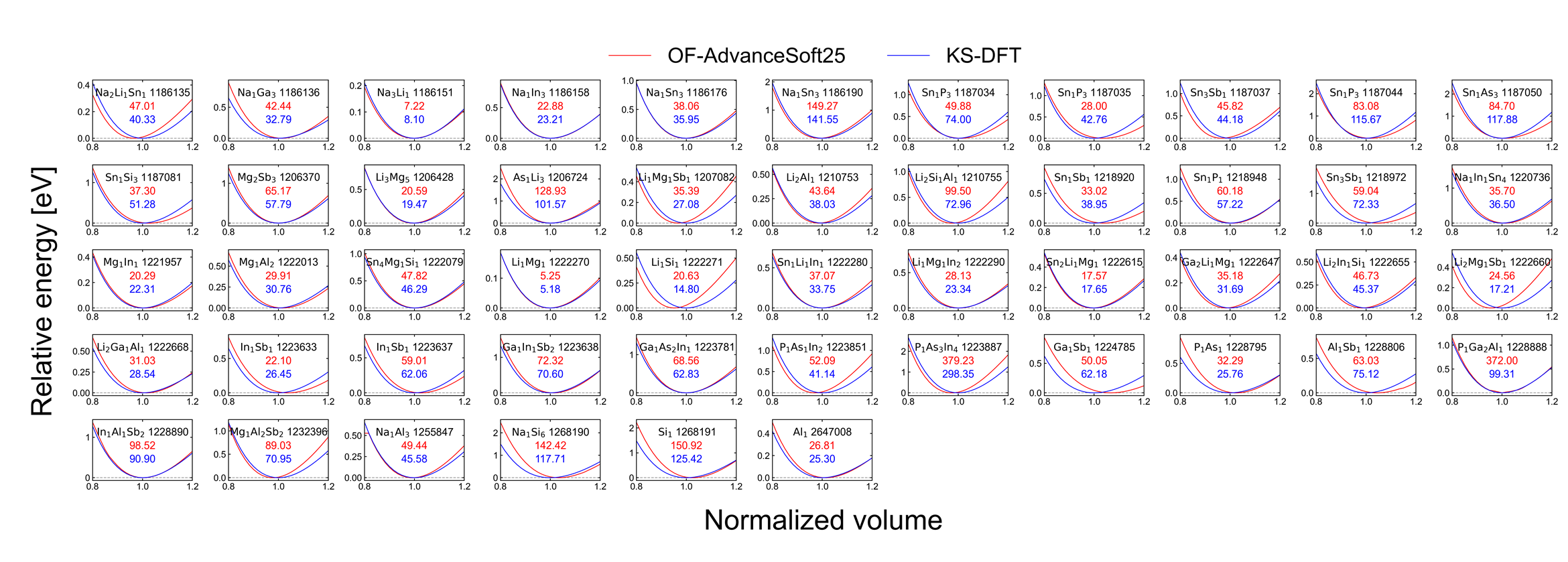
計算の結果として得られた各構造におけるエネルギー-体積曲線を以下の図に示します。 化学式の右側の数字は、Materials Projectにおけるその構造のIDを示しています。
また、以下の式を用いて、平衡体積におけるエネルギーの二階微分から体積弾性率を求めました。
図中の赤、青の数字がそれぞれAS25、KS-DFTの結果による体積弾性率の値(単位はGPa)に対応します。
|
|
|
|
| エネルギー-体積曲線と体積弾性率 |
上図では、AS25はほとんどの構造においてエネルギー-体積曲線を精度よく再現できており、高い精度と汎用性を持ち合わせていることがわかります。 また、体積弾性率のKS-DFTの結果に対する誤差を計算すると、平均絶対誤差は3.05 GPa、平均絶対相対誤差は8.26 %となり、定量的にも精度よく計算できていると言えます。
総括と展望#
本事例の結果から、AS25は、平衡状態からずれた系のエネルギー及び体積弾性率についても高精度に計算できることがわかりました。 このことから、AS25は弾性に関する各種物理量の予測や構造最適化計算にも応用可能であると考えられます。
また、従来KE汎関数のように系ごとにパラメータを調整することなく、単一の学習済みモデルAS25として種々の材料の物性予測に応用可能であることがわかりました。
今後は、教師データやモデルのアーキテクチャ、収束アルゴリズムの改善により更なる精度向上を行う予定です。