深層学習運動エネルギー汎関数AdvanceSoft25の精度ベンチマーク#

材料物性予測のための密度汎関数理論(DFT)計算の解法として最も広く知られているKohn-Sham DFT (KS-DFT)は、電子の軌道を用いる必要があるため、計算コストが系のサイズに対しておおよそ $O(N^3)$ で増大するという課題を抱えています。この課題を解決する手法として、軌道を使わずに電子密度を直接最適化するOrbital-Free DFT (OF-DFT)計算が提案されており、Advance/OF-DFTでは、この計算を実行することができます。 OF-DFTは、軌道を用いないことで計算コストが $O(N)$ でスケールし、大きなサイズの系に対しても高速な計算を実現します。

一方で、従来のOF-DFTは、計算精度を大きく左右する運動エネルギー汎関数として十分な精度を持つものが未知であったため、実用化には至っていませんでした。そこでアドバンスソフト株式会社では、独自の場の深層化アルゴリズムを適用した深層学習運動エネルギー汎関数AdvanceSoft25 (AS25)を開発し、Advance/OF-DFTに搭載しました。 AS25は、OF-DFTの最大のメリットである $O(N)$ の低い計算コストを維持しながら、従来の運動エネルギー汎関数よりも高精度な電子密度計算を可能とします。

本事例では、深層学習運動エネルギー汎関数AdvanceSoft25の計算精度のベンチマークを実施しました。

計算条件#

対象とする構造は、AS25の教師データセット¹のうちテストデータとして分離した、金属・絶縁体・スラブを含む129個の結晶構造です。

以下の条件で各構造に対してKS-DFT及びOF-DFTを実行し、電子密度分布、トータルエネルギー、形成エネルギー、表面エネルギーのKS-DFTに対する誤差を算出しました。

波動関数のカットオフエネルギー : 1350 eV
エネルギーの収束閾値 : 1×10^-4 eV
SCFの最大ステップ数 : 200
擬ポテンシャル : OEPP (27元素種²)
交換相関汎関数 : LDA
k点サンプリング : 0.05 Å^-1 (KS-DFT)
スメアリング幅 : ~ 0.7 eV ³ (KS-DFT)
プレコンディショナー : damping関数 (カットオフ半径 = 0.25 Å) ⁴ (OF-DFT)

KS-DFTにはQuantum ESPRESSO 6.7 (アドバンスソフト改修版)を使用しました。OF-DFTの運動エネルギー汎関数（KE汎関数）としては、AS25と既存のよく知られているTFλvW、LKT、HC⁵に加えて、比較用にAS25のアーキテクチャから場の深層化を取り除いて学習した非局所モデルのNL25、準局所モデルのSL25を用いて計算を行いました。

計算結果#

電子密度分布の予測精度#

以下の式で定義される電子密度の規格化された平均絶対誤差 (Normalized Mean Absolute Error (MAE))を、各構造に対して算出し、材料系ごとに平均をとったものを以下の棒グラフに示します。

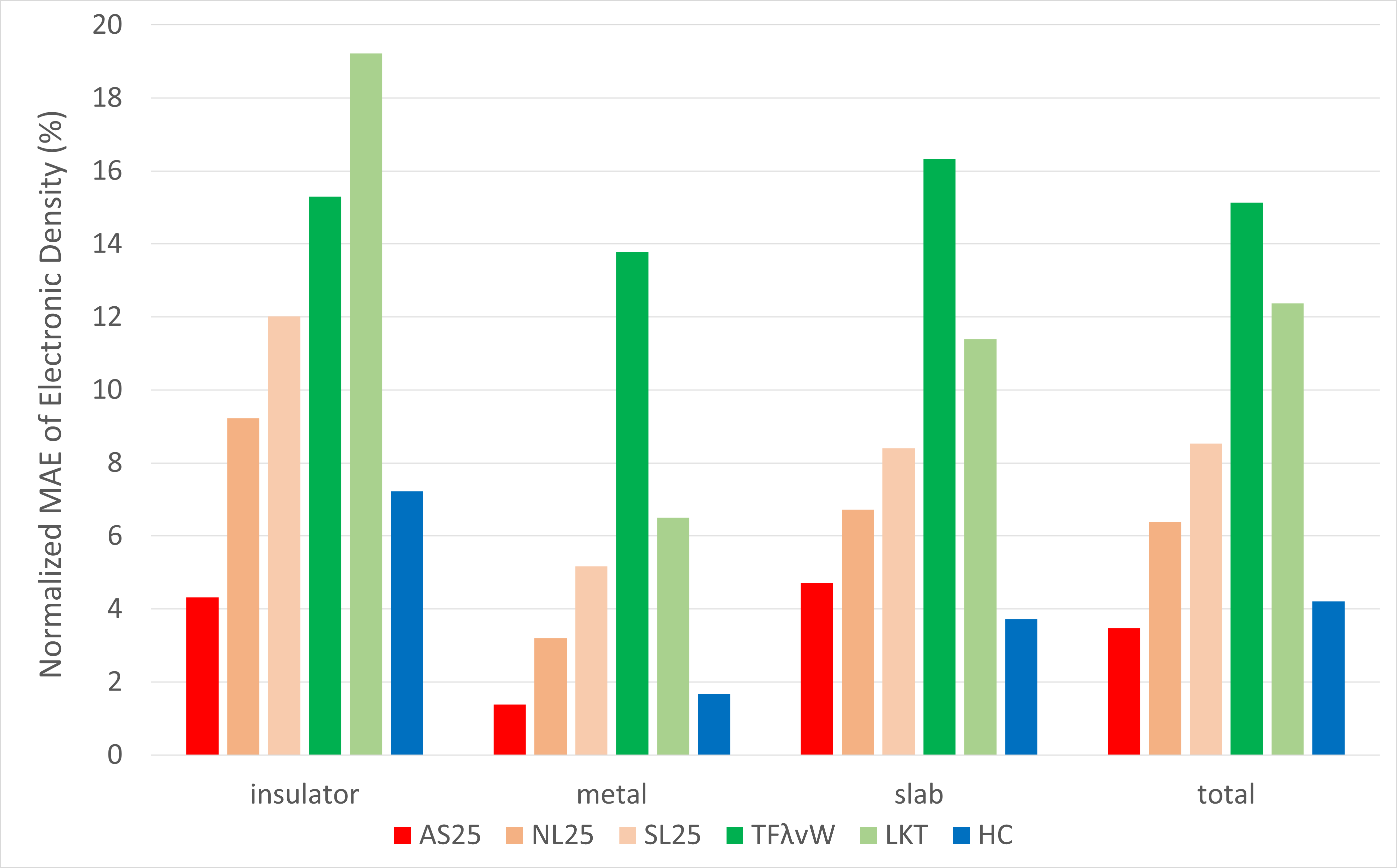
$\mathrm{Normalized\ MAE} = \frac{\sum_{i}^{n} | \rho^\mathrm{OF-DFT} (\boldsymbol{r}_i) - \rho^\mathrm{KS-DFT} (\boldsymbol{r}_i) |/n}{\sum_{i}^{n} \rho^\mathrm{KS-DFT} (\boldsymbol{r}_i)/n}$

全系についての結果を見ると、AS25のNormalized MAEが約3%と最も小さく、従来のいずれのKE汎関数よりも優れた電子密度予測精度を持つことがわかります。また、場の深層化を行っていないモデルのNL25, SL25と比較するとAS25の誤差はおよそ半分以下であり、場の深層化が精度向上に大きく寄与していることがわかります。

従来のKE汎関数では、バンドギャップを持つ絶縁体に対しては金属に比べて計算精度が低いことが知られています。実際に今回の結果にもその傾向があり、従来KE汎関数の中で最も優れているHCでも約7%の誤差があります。一方AS25の結果を見ると、同様の傾向はあるものの、絶縁体における誤差はHCのおよそ半分程度になっており、圧倒的に高い精度で電子密度を予測できていることがわかります。

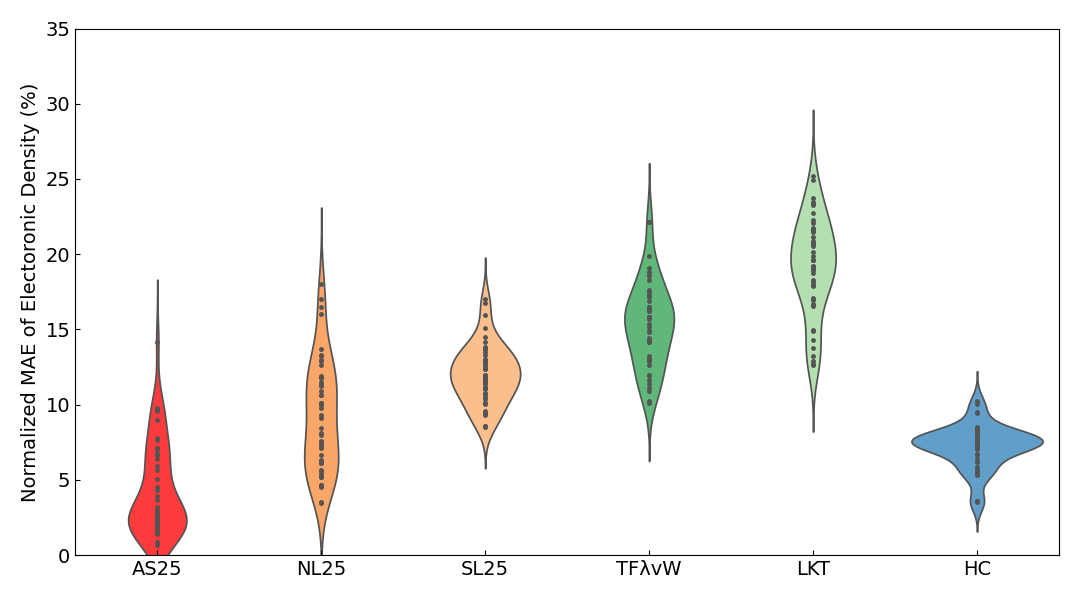
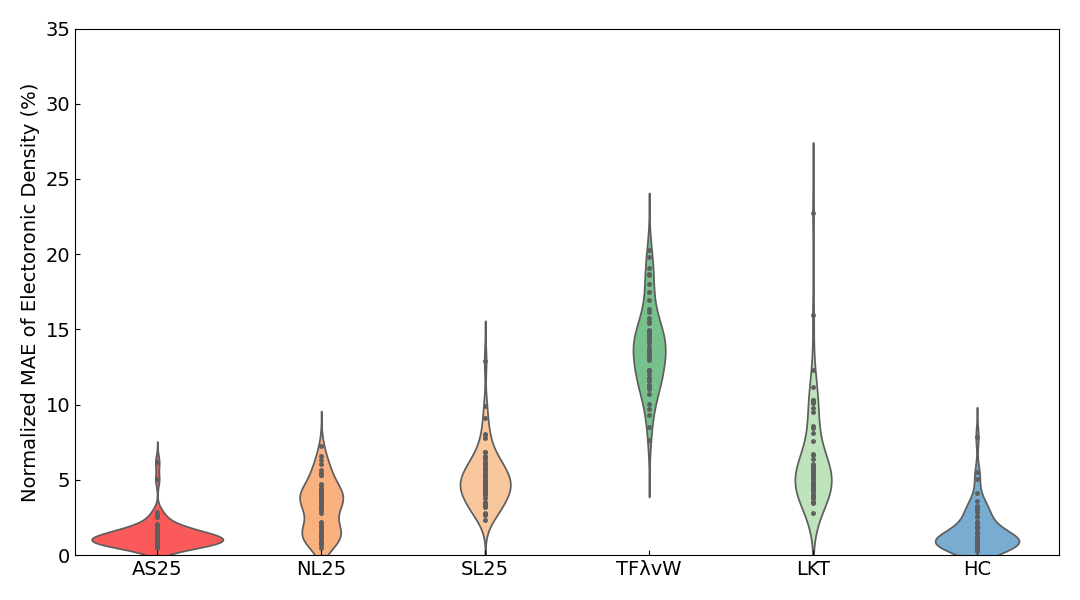
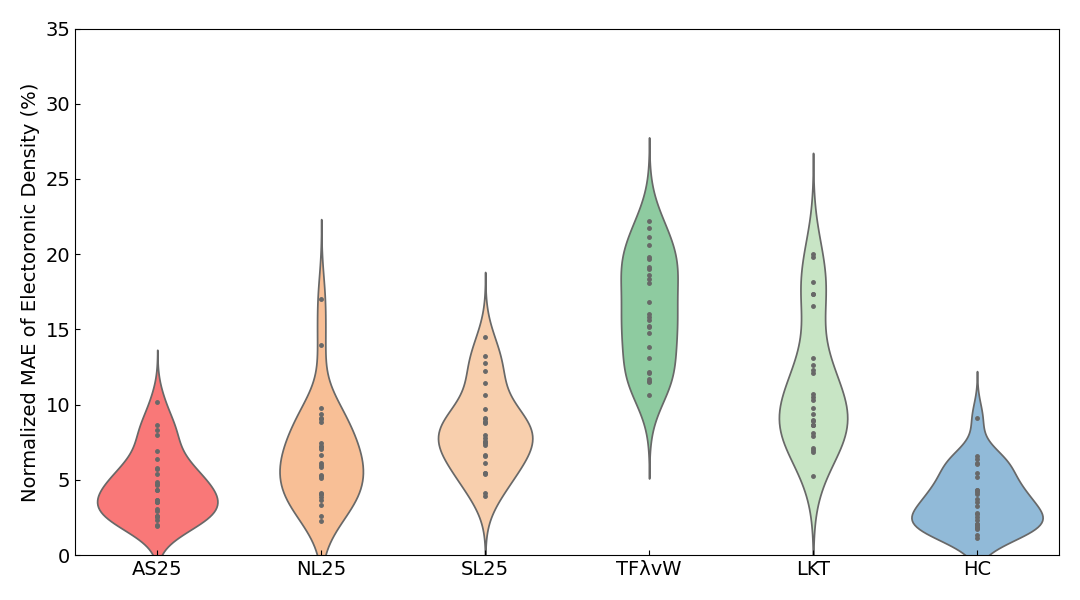
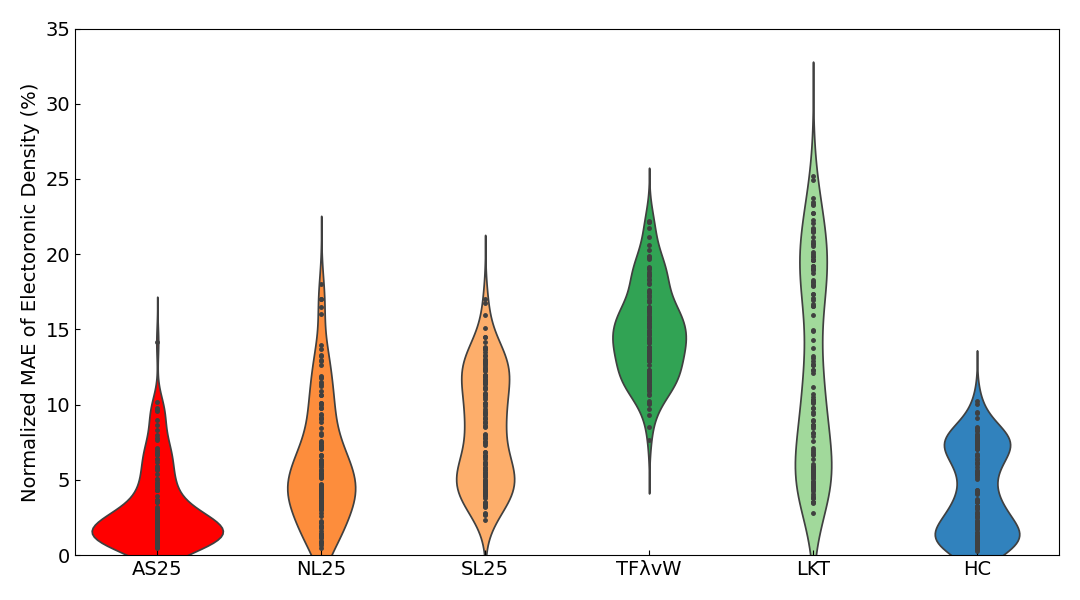
また、以下には電子密度のNormalized MAEのViolin plot⁶も示します。


insulator	metal	slab

total

絶縁体、金属、全系のいずれのViolin plotにおいても、AS25の結果が最も誤差の小さい領域に分布していことがわかります。また、スラブの結果については、誤差の平均を見るとAS25がHCにやや劣っていますが、Violin plotを見ると誤差の分布はほとんど同程度であることがわかります。

トータルエネルギーの予測精度#

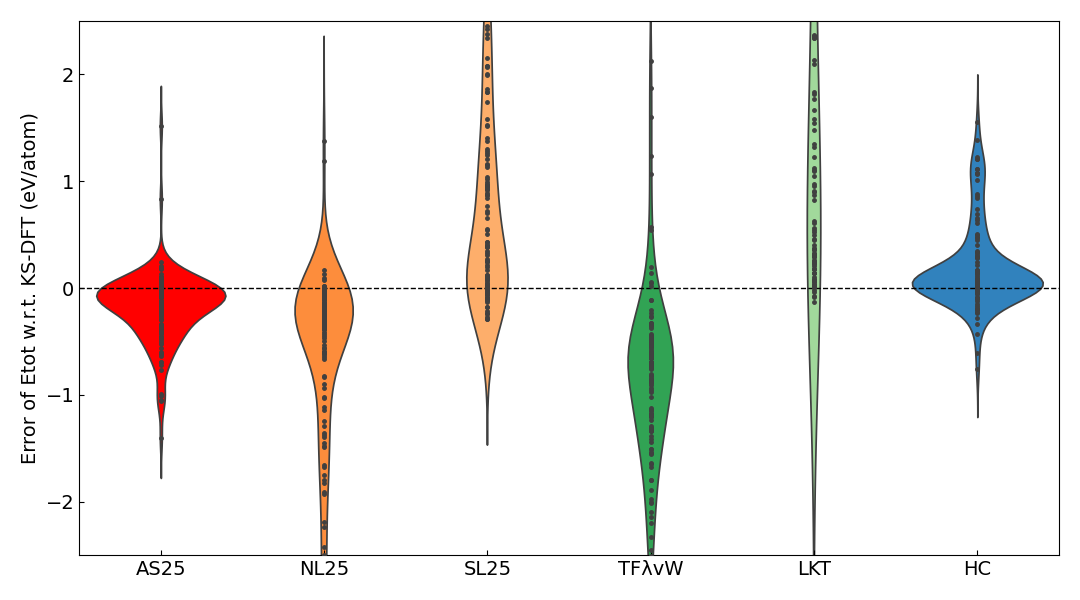
1原子当たりのトータルエネルギーについて、KS-DFTの結果に対するMAEを算出し、以下の表に示します。また、KS-DFTの結果に対する誤差のViolin plotも併せて示します。

MAE of Etot (eV/atom)
AS25	2.47×10^-1
NL25	6.69×10^-1
SL25	8.26×10^-1
TFλvW	1.02
LKT	2.89
HC	2.56×10^-1

表及びViolin plotからは、AS25のMAEが最も小さく、誤差の分布は0.1 eV/atom ~ -0.1 eV/atom付近に最も集中していることがわかります。

形成エネルギーの予測精度#

27元素の各標準状態の1原子当たりのエネルギー $E_i$ を計算し、テストデータ中の各構造に対して、以下の式で定義される形成エネルギーを算出しました。

$E_{\mathrm{f}} = \frac{1}{\sum_i n_i } \left( E_{\mathrm{total}} - \sum_i n_i E_i \right)$

ここで $E_{\mathrm{total}}$ 、 $n_i$ はそれぞれ対象となる構造のトータルエネルギー、含まれる元素 $i$ の原子数です。

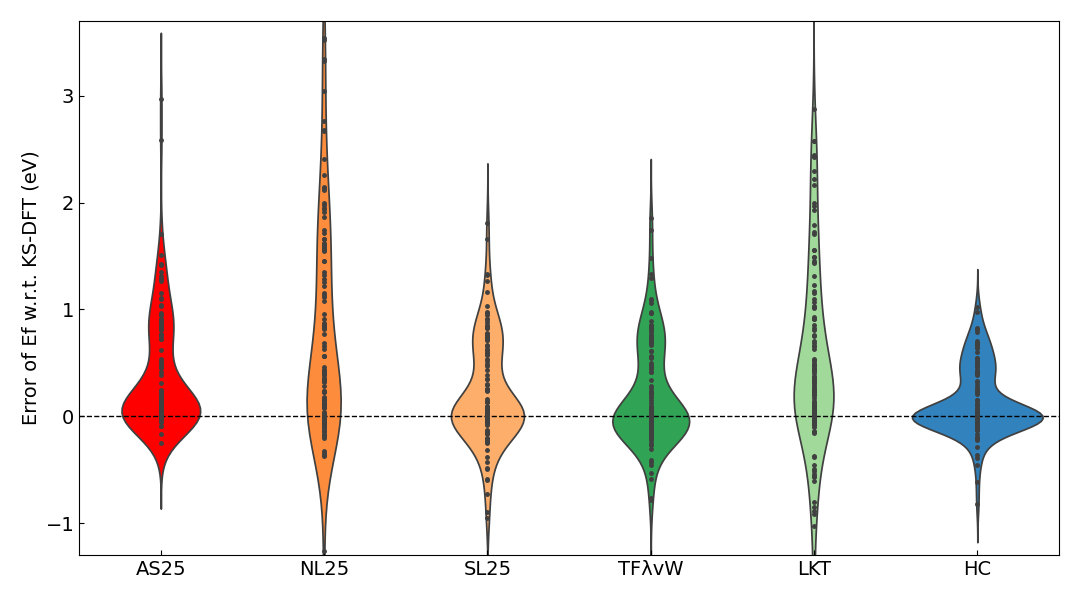
各KE汎関数で計算した形成エネルギーの、KS-DFTの結果に対するMAEを以下の表に示します。また、KS-DFTの結果に対する誤差のViolin plotも併せて示します。

MAE of Ef (eV)
AS25	3.99×10^-1
NL25	8.69×10^-1
SL25	3.69×10^-1
TFλvW	3.59×10^-1
LKT	7.09×10^-1
HC	2.18×10^-1

AS25の形成エネルギーのMAEはトータルエネルギーのMAEと同程度のオーダーになっており、Violin plotの分布もトータルエネルギーの場合と同様に0.1 eV/atom ~ -0.1 eV/atom付近に最も集中していることがわかります。なお、他のKE汎関数で、トータルエネルギーよりも形成エネルギーの方が誤差が改善しているのは、絶対値ではなく相対値を見ていることに起因すると考えられます。

表面エネルギーの予測精度#

テストデータ中の26個のスラブ構造のもととなったバルク構造のトータルエネルギー $E_{\text{bulk}}$ についても計算を行い、以下の式で定義される表面エネルギーを算出しました。

$E_{\text{surf}} = \frac{E_{\text{slab}} - E_{\text{bulk}}}{2A}$

ここで、 $E_{\text{slab}}$ 、 $A$ はそれぞれスラブ構造のトータルエネルギー、表面積です。

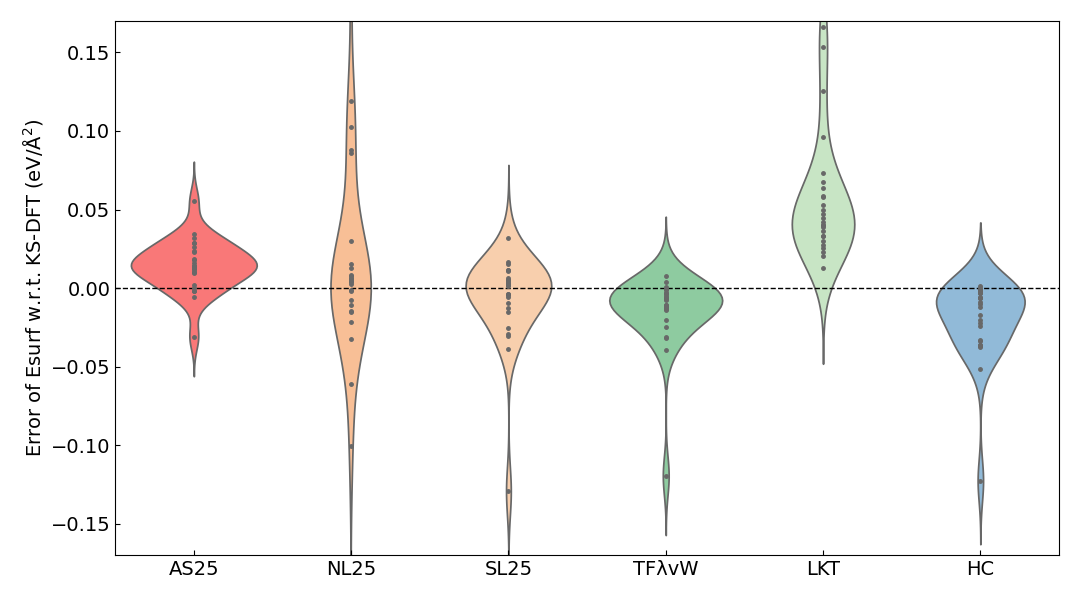
各KE汎関数で計算した表面エネルギーの、KS-DFTの結果に対するMAEを以下の表に示します。また、KS-DFTの結果に対する誤差のViolin plotも併せて示します。

MAE of Esurf (eV/Å²)
AS25	1.75×10^-2
NL25	3.76×10^-2
SL25	1.67×10^-2
TFλvW	1.58×10^-2
LKT	5.62×10^-2
HC	2.06×10^-2

AS25の表面エネルギーのMAEは1×10^-2 eV/Å²のオーダーに収まっており、誤差の分布は0 eV/Å² ~ 0.03 eV/Å²付近に最も集中していることがわかります。

総括と展望#

本事例の計算結果から、深層学習運動エネルギー汎関数 AdvanceSoft25 (AS25)の計算精度は、電子密度分布計算においてはいずれの従来KE汎関数よりも総合的に優れており、種々のエネルギー指標においても従来KE汎関数と同程度もしくはそれ以上の精度を持つことがわかりました。

また、教師データから分離したテストデータに対して高精度に計算できていることから、擬ポテンシャルの存在する範囲内では、どのような元素種の組み合わせに対しても汎用的に使用可能であることも示されました。さらに、従来KE汎関数では不得意とされていた絶縁体への応用が十分可能であることもわかりました。

今後は、教師データの拡充や深層化の層数の増加などによる汎関数の精度向上、電子密度の最適化アルゴリズムの改良などによって更なる精度向上が期待できると考えられます。また、対応する擬ポテンシャルを全元素へと拡充し、より汎用的に使用できるようなアップデートも予定しています。