[Advance/NeuralMD Pro] Neural Network力場のGPU化#

2022年9月に、Advance/NeuralMDをGPU化したAdvance/NeuralMD Proをリリースする。Neural Networkの学習過程およびLAMMPSでの分子動力学計算がGPU化されており、いずれもMPIと併用することでマルチGPUおよびマルチノードのマシン環境に対応している。この記事では、GPU化の仕組みを紹介する。GPUによるベンチマーク結果については、別記事にて紹介する。

Neural Network力場の計算では、下図のような多層パーセプトロンを用いた手続きにてエネルギーおよび力を計算する。
先ずは、①対称関数 $𝐺_{𝑖,𝛼}$ および隣接原子座標 $𝑹_{𝑗}$ による微分 $\frac{\partial\, 𝐺_{𝑖,𝛼}}{\partial\, 𝑹_{𝑗}}$ を計算する。これを②順方向に伝搬させてエネルギー $𝐸_{𝑖}$ を計算した後、③逆方向への伝搬にて微分 $\frac{\partial\, 𝐸_{𝑖}}{\partial\, 𝐺_{𝑖,𝛼}}$ を計算する。最後に、④隣接原子間で $\sum_{a} \frac{\partial\, 𝐺_{𝑖,𝛼}}{\partial\, 𝑹_{𝑗}} \frac{\partial\, 𝐸_{𝑖}}{\partial\, 𝐺_{𝑖,𝛼}}$ を計算して原子𝑖が𝑗に及ぼす力 $𝑭_{𝑖,𝑗}=\frac{\partial\, 𝐸_{𝑖}}{\partial\, 𝑹_{𝑗}}$ を計算する。

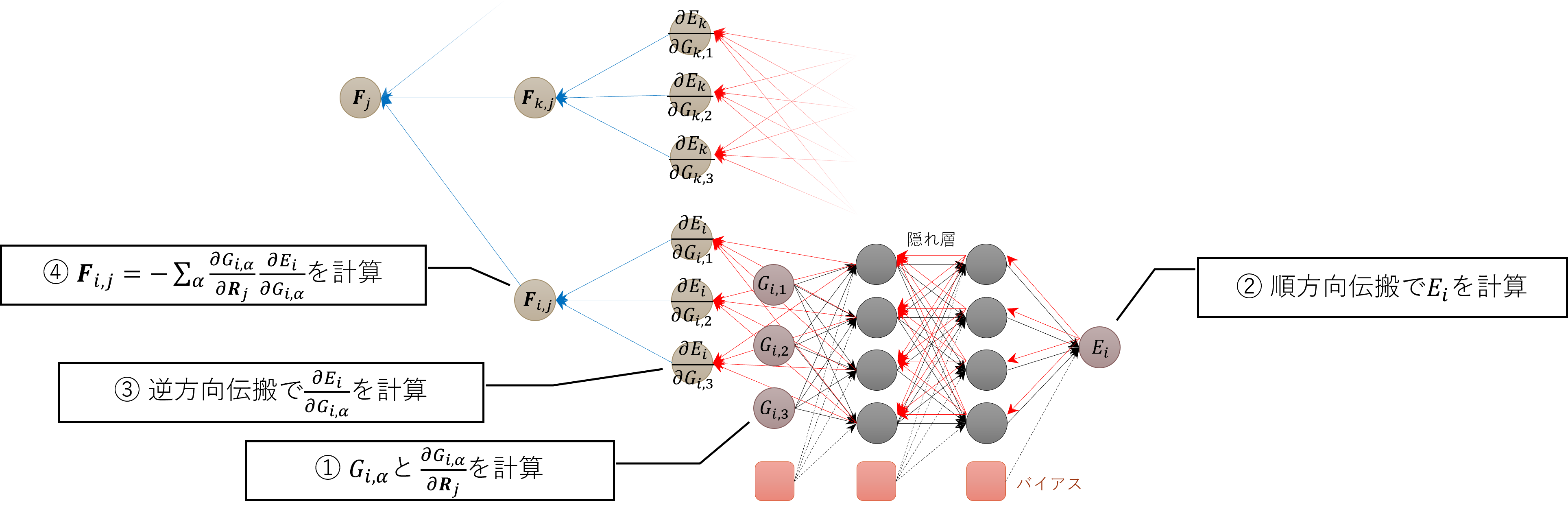
最も計算コストが高いのは、①の対称関数とその微分の計算である。②および③のNeural Network内の伝搬過程は行列‐行列の積(Level-3 BLAS)にて遂行されるのだが、他の処理に比べると計算コストは極めて低い。
④は対称関数に次いで２番目に計算コストが高い。 $𝑭_{𝑖,𝑗}$ は $𝑖$ を固定することで、 $\frac{\partial\, 𝐺_{𝑖,𝛼}}{\partial\, 𝑹_{𝑗}}$ を行列、 $\frac{\partial\, 𝐸_{𝑖}}{\partial\, 𝐺_{𝑖,𝛼}}$ をベクトルとしてLevel-2 BLASにて計算される。原子 $𝑗$ に働く力は、ニュートンの第三法則を適用することで

$𝑭_{𝑗}=\sum_{𝑖} 𝑭_{𝑖,𝑗} =𝑭_{𝑗,𝑗}+\sum_{𝑖\ne 𝑗} 𝑭_{𝑖,𝑗}=−\sum_{𝑖\ne 𝑗} 𝑭_{𝑗,𝑖}+\sum_{𝑖\ne 𝑗} 𝑭_{𝑖,𝑗}=\sum_{𝑖\ne 𝑗}\{−𝑭_{𝑗,𝑖}+𝑭_{𝑖,𝑗}\}$

と計算される。最右辺の通り、 $𝑭_{𝑗,𝑗}$ は明示的に計算する必要はない。また、 $𝑭_{𝑖,𝑗}$ はビリアル応力の計算にも利用される。

さらに、Neural Networkの学習過程においては、⑤力 $𝑭_{𝑖}$ の誤差を計算する必要がある。力はNeural Networkの一階微分として計算されるため、その誤差を計算するには二階微分が要求される。この二階微分の計算には多数回のLevel-2およびLevel-3 BLASが実行されるため、④以上の計算コストが掛かり、学習過程における計算時間の90%以上を占める。

Neural Networkの学習過程においては、最初に一度だけ全ての構造における対称関数 $𝐺_{𝑖,𝛼}$ とその座標微分 $\frac{\partial\, 𝐺_{𝑖,𝛼}}{\partial\, 𝑹_{𝑗}}$ を計算する(①)。その後、各エポックにおいて②〜⑤の処理を実行してエネルギーおよび力の誤差を計算する。①についてはGPU化しているのだが、計算回数がただ一度だけなので計算時間全体の短縮には大きく寄与しない。重要なのは、②〜⑤の高速化を図ることである。ただし、②および③は元より低コストであるため、GPU化はせずにホスト側(CPU)で処理する。④は最大のボトルネックでは無いものの、無視できない程度の計算時間を要する。しかしながら、学習過程においては $\frac{\partial\, 𝐺_{𝑖,𝛼}}{\partial\, 𝑹_{𝑗}}$ のデータ容量が大きく(100 GB以上となることもある)、GPUのグローバルメモリーに載せることは難しい。このため、最大のボトルネックであるNeural Networkの二階微分の計算(⑤)のみをGPU化する。⑤はLevel-2およびLevel-3 BLASの計算であるため、cuBLASを使うことで容易にGPU化できる。

学習過程のGPU化#

②〜④はCPUで処理され、⑤はGPUで処理される。⑤がGPUで高速化されたことにより、②〜④の計算時間も無視できなくなる。このため、そのまま計算を実行すると十分な高速化が期待できない可能性がある。そこで、MPIによるプロセス並列を併用することでさらなる性能向上を図る。例えば、MPIで４プロセスを起動した場合、１エポック当たり各プロセスは下図のように動作する。エポックの開始から⑤が完了するまでプロセス間の通信が存在しないため、この間は各プロセスは非同期で動作できる。そうすると、あるプロセスがCPUで処理している間に別のプロセスがGPUにて計算を実施するという状況が起こる。GPUに対して物理コア数を超過するスレッド数を流すことでGPUの稼働率が上昇し、相対的にCPUでの処理時間を低減できる。その結果、学習過程全体が十分に高速化される。経験上、GPU１デバイス当たり２〜４つのMPIプロセスがあれば十分である。また、CPUにおける処理はOpenMPでスレッド並列されている(つまり、CPUにおいてはMPI＋OpenMPハイブリッド並列である)。

LAMMPSによるMD計算のGPU化#

学習済みのNeural Network力場を使ってMD計算を実施するときも計算コストが高いため、GPUによる高速化が必要である。Advance/NeuralMDではMD計算にLAMMPSを使用している。Neural Network力場の計算部分は当社独自実装である。MD計算では、各MDステップにおいて①〜④の処理が必要である。学習過程と同様に②と③はCPUで処理する。対称関数の計算(①)と力の計算(④)をGPU化する。 $\frac{\partial\, 𝐺_{𝑖,𝛼}}{\partial\, 𝑹_{𝑗}}$ のデータ容量は学習過程に比べると大きくないため、①で生成した $\frac{\partial\, 𝐺_{𝑖,𝛼}}{\partial\, 𝑹_{𝑗}}$ をGPUのグローバルメモリーに保持したまま、④の計算にて利用する。当該データはGPU内部だけで扱われるため、ホストへの転送は不要である。MD計算では①が最大のボトルネック(計算時間の95%以上)であるが、対称関数の計算はGPUとの相性が良く大幅な高速化が期待できる。また、学習過程と同様に、１デバイス当たり２〜４プロセスのMPI並列を適用することで計算効率が向上する。

対称関数計算のGPU化#

対称関数の計算をGPU化する方法を紹介する。対称関数には動径成分 $𝐺_{𝑖,𝛼}^{rad}$ と角度成分 $𝐺_{𝑖,𝛼}^{ang}$ があるのだが、先ずは $𝐺_{𝑖,𝛼}^{rad}$ について説明する。 $𝐺_{𝑖,𝛼}^{rad}$ は一般に

$𝐺_{𝑖,𝛼}^{rad}=\sum_{𝑗\ne 𝑖} 𝐺_{𝛼}^{rad} (𝑹_{𝑖},𝑹_{𝑗})$

として計算される。右辺は全ての隣接原子 $𝑗$ についての総和である。原子座標についての微分は

$\frac{\partial\, 𝐺_{𝑖,𝛼}^{rad}}{\partial\, 𝑹_{𝑗}}=\frac{\partial\, 𝐺_{𝛼}^{rad} (𝑹_{𝑖},𝑹_{𝑗}) }{\partial\, 𝑹_{𝑗}}$

である。 $𝑗\ne 𝑖$ であれば、 $𝑖$ および $𝑗$ をそれぞれCUDAのブロックおよびスレッドに割り当てることで容易にGPU化できる。対称関数の自由度 $𝛼$ については、ブロック当たりのスレッド数が適切な値となるように $𝛼$ を因数分解して $𝑖$ および $𝑗$ に直積される。また、 $𝑗=𝑖$ の場合にはスレッド間の依存関係が発生するのだが、当該項はあえて計算しないことで性能向上を図る。当該項 $\frac{\partial\, 𝐺_{𝑖,𝛼}^{rad}}{\partial\, 𝑹_{𝑖}}$ は明示的に計算せずとも、 $𝐺_{𝛼}^{rad} (𝑹_{𝑗},𝑹_{𝑖})=𝐺_{𝛼}^{rad} (𝑹_{𝑖},𝑹_{𝑗})$ によりニュートンの第三法則が成り立つため、事後的にその寄与を取り込むことが出来るのである。

次に、角度成分 $𝐺_{𝑖,𝛼}^{ang}$ について説明する。 $𝐺_{𝑖,𝛼}^{ang}$ の計算には少々の工夫が必要である。 $𝐺_{𝑖,𝛼}^{ang}$ は一般に

$𝐺_{𝑖,𝛼}^{ang}=\sum_{𝑗\ne 𝑖} \sum_{𝑘<𝑗} 𝐺_{𝛼}^{ang} (𝑹_{𝑖},𝑹_{𝑗},𝑹_{𝑘})$

として計算される。右辺の内側の総和により $𝑗$ と $𝑘$ に依存関係が生じるため、GPU化が難しい。そこで $𝐺_{𝛼}^{ang} (𝑹_{𝑖},𝑹_{𝑘},𝑹_{𝑗})=𝐺_{𝛼}^{ang} (𝑹_{𝑖},𝑹_{𝑗},𝑹_{𝑘})$ の関係を利用して、

$𝐺_{𝑖,𝛼}^{ang}=\frac{1}{2} \sum_{𝑗\ne 𝑖} \sum_{𝑘\ne 𝑖} 𝐺_{𝛼}^{ang} (𝑹_{𝑖},𝑹_{𝑗},𝑹_{𝑘})$

のように式を変形する。計算量は2倍となるものの、 $𝑗$ と $𝑘$ の依存関係が消失する。微分については

$\frac{\partial\, 𝐺_{𝑖,𝛼}^{ang}}{\partial\, 𝑹_{𝑗}}=\frac{1}{2} \left[ \sum_{𝑘\ne 𝑖} \frac{\partial\, 𝐺_{𝛼}^{ang} (𝑹_{𝑖},𝑹_{𝑗},𝑹_{𝑘})}{\partial\, 𝑹_{𝑗}}+\sum_{𝑘\ne 𝑖} \frac{\partial\, 𝐺_{𝛼}^{ang} (𝑹_{𝑖},𝑹_{𝑘},𝑹_{𝑗})}{\partial\, 𝑹_{𝑗}} \right]\\=\sum_{𝑘\ne 𝑖} \frac{\partial\, 𝐺_{𝛼}^{ang} (𝑹_{𝑖},𝑹_{𝑗},𝑹_{𝑘})}{\partial\, 𝑹_{𝑗}} \qquad\qquad\qquad\qquad\qquad$

となる。そうすると状況は動径成分の場合と同様である。つまり、 $𝑖$ をCUDAのブロック、 $𝑗$ をCUDAのスレッドに割り当てるのである。ただし、各スレッドは $\sum_{𝑘\ne 𝑖} 𝐺_{𝛼}^{ang} (𝑹_{𝑖},𝑹_{𝑗},𝑹_{𝑘})$ および $\sum_{𝑘\ne 𝑖} \frac{\partial\, 𝐺_{𝛼}^{ang} (𝑹_{𝑖},𝑹_{𝑗},𝑹_{𝑘})}{\partial\, 𝑹_{𝑗}}$ の計算を担当する。スレッド内で $𝑘$ に関するループがあるのだが、ループの内部で各スレッドが全ての $𝑹_{𝑘}$ にアクセスする。 $\{𝑹_{𝑘}\}$ は $\{𝑹_{𝑗}\}$ と等価であるため、各ブロックにて $\{𝑹_{𝑗}\}$ を共有メモリーに載せることでグローバルメモリーへのアクセス頻度を低減させて高速化を図る。また、 $𝑖=𝑗$ の場合における $\frac{\partial\, 𝐺_{𝑖,𝛼}^{ang}}{\partial\, 𝑹_{𝑖}}$ の計算においても、動径成分の場合と同様にニュートンの第三法則が利用できる。

対称関数がChebyshev多項式の場合、漸化式の形式で計算すると $𝛼$ に関する依存関係が発生するため、あえてコサインを使って非効率に計算することでGPU化しやすくするという工夫も必要である。

[Advance/NeuralMD Pro] Neural Network力場のGPU化#

Neural Network力場の計算手続き#

学習過程のGPU化#

LAMMPSによるMD計算のGPU化#

対称関数計算のGPU化#

関連ページ#