ハイブリッド汎関数法を用いた半導体のバンドギャップ計算#

PHASE logo

半導体材料のバンドギャップは、その電気的・光学的特性を決定する最も重要な物性値の一つです。第一原理計算における局所密度近似(LDA)や一般化勾配近似(GGA)は、多くの物性を高精度に予測できますが、バンドギャップについては実験値よりも大幅に小さい値を算出する（過小評価）という問題が知られています。この問題を解決する手法として、ハイブリッド汎関数法が注目されています。本解析では、第一原理計算ソフトウェアAdvance/PHASEに搭載されているハイブリッド汎関数(HSE06)を用い、さまざまな半導体材料のバンドギャップを高精度に計算した事例をご紹介します。

Keywords: 第一原理計算, バンドギャップ, ハイブリッド汎関数, HSE06, 密度汎関数理論, 状態密度

ハイブリッド汎関数法(HSE06)とは#

ハイブリッド汎関数法 [1] は、電子間の交換相関相互作用の評価において、GGA (PBE)に厳密交換相互作用を一定の割合で混合する手法です。これにより、電子の自己相互作用が打ち消され、バンドギャップの過小評価が大幅に改善されます。

HSE汎関数における交換相関エネルギーは、以下の式で表されます：

$E_\text{xc}^\text{HSE} = \alpha E_\text{x}^\text{SR, HF}(\omega) + (1-\alpha)E_\text{x}^\text{SR, PBE}(\omega) + E_\text{x}^\text{LR, PBE}(\omega) + E_\text{c}^\text{PBE}$

この式の意味は、遮蔽パラメータ $\omega$ を用いて電子間の相互作用を短距離(SR)成分と長距離(LR)成分に分割し、短距離部分の交換エネルギーをHartree-Fock (HF)厳密交換エネルギー $E_\text{x}^\text{SR, HF}$ とPBE汎関数の交換エネルギー $E_\text{x}^\text{SR, PBE}$ で混合（ハイブリッド化）する、というものです。長距離部分の交換エネルギーと全ての相関エネルギー $E_\text{c}^\text{PBE}$ はPBE汎関数で計算します。バンドギャップの補正に特に重要な短距離の相互作用に計算コストの高い厳密交換を適用し、長距離では計算コストの低いPBEを用いることで、精度と計算効率のバランスを取っています。

特にHSE06汎関数は、この混合パラメータ $\alpha$ を0.25、遮蔽パラメータ $\omega$ を0.106 bohr^-1に設定したもので、多くの物質で高い精度を示すことが知られています。

とはいえ、HSE06法は通常のGGA計算と比較して非常に多くの計算時間を要するため、適用する際には計算リソースを考慮する必要があります。

計算手順#

ハイブリッド汎関数計算は、一般的に以下の2ステップで行います。

まず、計算コストの低いPBE汎関数を用いて通常のセルフコンシステント計算(SCF)を行い、系の安定な電子状態（波動関数と電荷密度）を求めます。
次に、ステップ1で得られた波動関数と電荷密度を初期値として用い、HSE06汎関数による高精度なSCF計算を実行します。
最後に、得られた電子状態から状態密度(DOS)を計算し、価電子帯の上端から伝導帯の下端までのエネルギー差としてバンドギャップを評価します。DOS計算には、ギャップ値を定量的に評価する上で精度の高い四面体法を用いています。

本解析に用いた主な計算条件は表1に示します。

表1.　計算条件

項目	設定
擬ポテンシャル	ウルトラソフト（一部元素はノルム保存）擬ポテンシャル
波動関数カットオフエネルギー	25 Rydberg
k点分割数	各物質で収束性が得られるように十分に設定
ハイブリッド汎関数	HSE06 (デフォルトパラメータ: α=0.25, ω=0.106)

計算結果と考察#

図1に、代表的な例として3C-SiCの状態密度(DOS)を示します。(a)のPBE汎関数による結果ではバンドギャップが狭く評価されていますが、(b)のHSE06汎関数を用いることでギャップが大きく広がり、実験値 [2] に近い状態が再現されていることが視覚的にわかります。

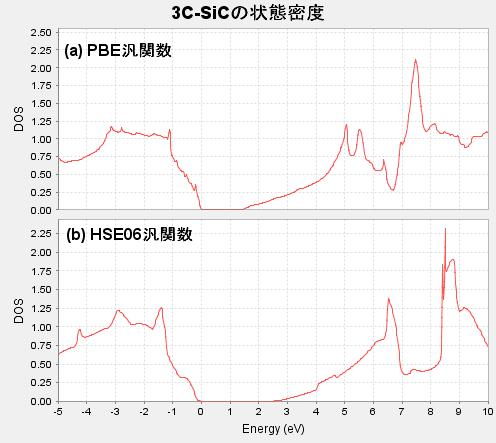
Density of states for 3C-SiC
図1.　(a)PBE汎関数および(b)HSE06汎関数で計算された3C-SiCの状態密度。

図2には別の例としてAlAsの状態密度を示します。こちらも3C-SiCと同様の傾向が見られ、PBE汎関数（オレンジ線）と比較してHSE06汎関数（青線）ではバンドギャップが大きく開いています。HSE06による計算値は、PBEの計算値よりも実験値 [2] に近く、HSE06の有効性がここでも確認できます。

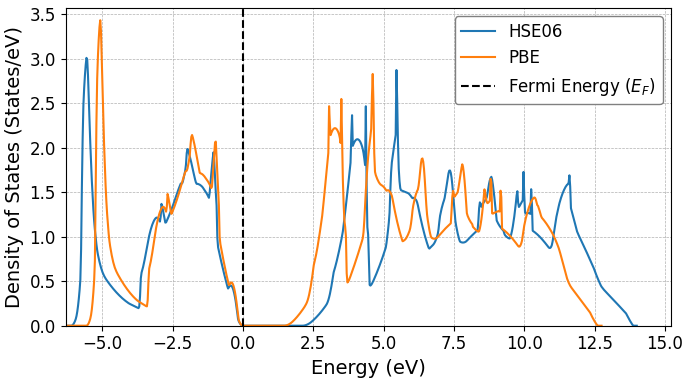
Density of states for AlAs
図2.　PBE汎関数およびHSE06汎関数で計算されたAlAsの状態密度の比較。

表2に、さまざまな半導体材料について、PBE汎関数、HSE06汎関数で計算したバンドギャップと実験値 [2] をまとめました。

表2.　各種半導体のバンドギャップ計算値と実験値 (eV)

物質	PBE (eV)	HSE06 (eV)	実験値 (eV)
Si	0.67	1.25	1.17
C (Diamond)	4.01	5.25	5.5
3C-SiC	1.25	2.20	2.36
4H-SiC	2.12	3.05	3.23
6H-SiC	1.91	2.91	3.00
AlP	1.69	2.40	2.45
AlAs	1.45	2.11	2.16
GaP	1.74	2.40	2.26
GaAs	0.62	1.59	1.43
TiO₂ (Rutile)	1.63	3.06	3.0
ZnO	0.62	1.23	3.37

表2から明らかなように、PBE計算ではすべての物質でバンドギャップが実験値より大幅に小さくなっています。一方、HSE06計算では、ほとんどの系で実験値と非常によく一致しており、バンドギャップの過小評価が劇的に改善されていることが確認できます。特に、SiC、AlAs、TiO₂などでは、実験値を高い精度で再現できています。

ただし、ZnOに代表される亜鉛(Zn)を含む化合物では、HSE06を用いても依然として実験値を大幅に過小評価する傾向が見られました。この現象は、Znの3d電子の扱いの難しさに起因するもので、計算材料科学の分野では広く知られた共通認識です。実際、多くの研究でこの課題が報告されており、例えば文献 [3] では、HSE汎関数の厳密交換項の混合比αを標準の0.25から0.375に調整することで、バンドギャップや格子定数を実験値とよく一致させられることが示されています。このように、標準的な手法で再現が難しい特定の系に対しては、パラメータを調整するなどのアプローチが有効な場合があります。

まとめ#

本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、ハイブリッド汎関数法(HSE06)が半導体材料のバンドギャップ予測に極めて有効であることを示しました。従来のLDA/GGA法が抱えるバンドギャップの過小評価の問題を大幅に改善し、多くの材料で実験値に近い結果を得ることができます。計算コストは非常に高いものの、デバイス設計や新材料探索において正確なバンドギャップ情報が不可欠な場面で、HSE06法は信頼性の高い予測を可能にする強力なツールとなります。

参考文献#

J. Heyd, G. E. Scuseria, and M. Ernzerhof, "Hybrid functionals based on a screened Coulomb potential", J. Chem. Phys. 118, 8207 (2003).
M. Levinstein, S. Rumyantsev and M. Shur, Handbook Series on Semiconductor Parameters, World Scientific, 1999.
F. Oba, A. Togo, I. Tanaka, J. Paier, and G. Kresse, "Defect energetics in ZnO: A hybrid Hartree-Fock density functional study", Phys. Rev. B 77, 245202 (2008).