ワークフロー構築と高精度な材料物性予測：圧電定数#

物質に力を加えると電圧が発生し、逆に電圧をかけると変形する「圧電効果」は、センサーやアクチュエーター、フィルターなど現代のエレクトロニクスに不可欠な現象です。この特性を支配する「圧電定数」を第一原理計算から正確に予測することは、新しい圧電材料を設計する上で極めて重要です。しかし、その計算は複数の物理現象が絡み合うため、非常に複雑で手順も多いという課題がありました。本解析では、第一原理計算ソフトウェアAdvance/PHASEのワークフロー機能を用いて、この複雑な計算手順を簡略化し、その精度を検証します。

Keywords: 第一原理計算, 圧電効果, 圧電定数, DFT, ワークフロー

圧電定数計算の「複雑さ」とは？#

圧電定数 ( $e_{ij}$ ) は、結晶にひずみを加えた際に生じる分極の変化として定義されます。この応答は、大きく分けて2つの物理現象の和として表されます。

イオン固定項 (Clamped-ion term): 結晶格子が変形する際に、イオンの位置が相対的に固定されていると仮定した場合の電子雲の応答。電子の分極のみを考慮します。
内部ひずみ項 (Internal strain term): 格子が変形するのに応答して、結晶内部のイオンが安定な位置へと再配置（緩和）することによるイオン分極の変化。

表1のAlNのe₃₃の計算結果を見ると、負となるイオン固定項と、大きな正の値をとる内部ひずみ項が、互いに逆符号となっていることが分かります。最終的な圧電定数は、これらの大きな値の打ち消し合いによって決まるため、各項を非常に高い精度で計算する必要があります。

表1.　AlNの圧電定数e₃₃の計算内訳 (C/m²)

イオン固定項	内部ひずみ項	合計 (計算値)	実験値 [1]
-0.398	2.004	1.607	1.55

さらに、これらの項を算出するには、セル最適化を含む構造最適化、フォノン計算（原子の変位）、ベリー位相理論に基づく分極計算、格子ひずみ下での応力計算など、多岐にわたる計算を正しい手順で実行する必要があり、専門家にとっても手間のかかる複雑なタスクでした。

課題解決 - 「ワークフロー機能」による計算手順の簡略化#

この「複雑さ」という課題を解決するのが、Advance/PHASEに搭載されたワークフロー機能です。この機能は、複雑な計算手順の構築を自動化し、ユーザーの負担を劇的に軽減します。

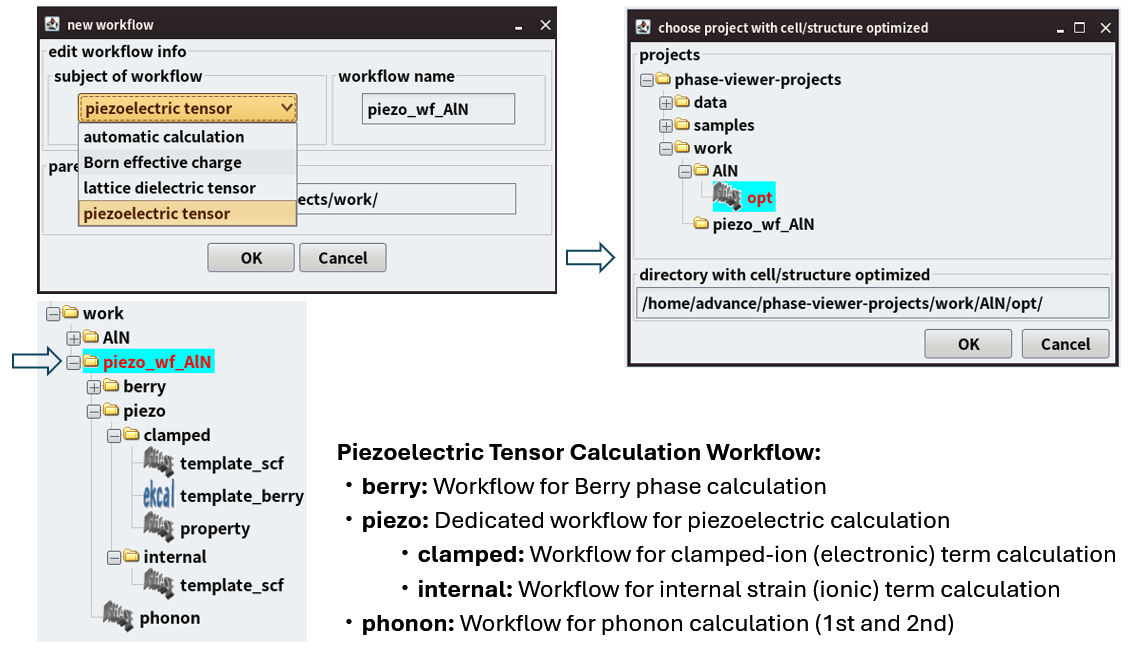
図1.　GUIから「piezoelectric tensor」を選択するだけで、複雑な計算フローが自動的に構築されます。

図1に示すように、ユーザーはGUI上で計算したい物性（ここでは「piezoelectric tensor」）を選択するだけで、必要な一連の計算プロジェクト（構造最適化、フォノン計算、ベリー位相計算、圧電項計算など）が、正しい依存関係を持って自動的に生成されます。従来は手作業で多数のインプットファイルを作成し、計算手順を管理する必要がありましたが、この機能により、計算設定のミスが低減され、煩雑な手作業を大幅に削減して信頼性の高い圧電定数計算に着手できるようになります。

計算精度の検証 - 実在圧電体との比較#

本手法で計算された圧電定数が、実際にどの程度の精度を持つのかを検証します。ここでは、代表的な圧電材料であるウルツ鉱型窒化物・酸化物と、強力な圧電特性で知られるペロブスカイト型強誘電体を対象としました。

ウルツ鉱型圧電体 (AlN, GaN, ZnO)#

窒化アルミニウム(AlN)、窒化ガリウム(GaN)、酸化亜鉛(ZnO)は、高周波フィルターなどで広く利用される代表的な圧電材料です。表2に計算結果と実験値 [1-3] を示します。

表2.　ウルツ鉱型材料の圧電定数の比較 (C/m²)

物質	成分	PHASE 計算値	実験値
AlN	e₃₁	-0.651	-0.58
	e₃₃	1.607	1.55
	e₁₅	-0.345	-0.48
GaN	e₃₁	-0.673	-
	e₃₃	0.932	0.44～1.0
	e₁₅	-0.242	-
ZnO	e₃₁	-0.592	-0.35～-0.62
	e₃₃	0.999	0.96～1.56
	e₁₅	-0.384	-0.35～-0.59

ペロブスカイト型強誘電体 (BaTiO₃, PbTiO₃)#

チタン酸バリウム(BaTiO₃)やチタン酸鉛(PbTiO₃)は、巨大な圧電応答を示すことで知られる強誘電体材料です。これらの複雑な酸化物においても、計算結果は実験値 [4, 5]の範囲とよく一致しています（表3）。

表3.　ペロブスカイト型材料の圧電定数の比較 (C/m²)

物質	成分	PHASE 計算値	実験値
BaTiO₃	e₃₃	3.725	3.65
PbTiO₃	e₃₃	3.969	3.35～6.50

図2に、主要な圧電成分であるe₃₃の計算値と実験値を比較したグラフを示します。いずれも実験値とよく一致しており、本手法の精度の高さが示されています。

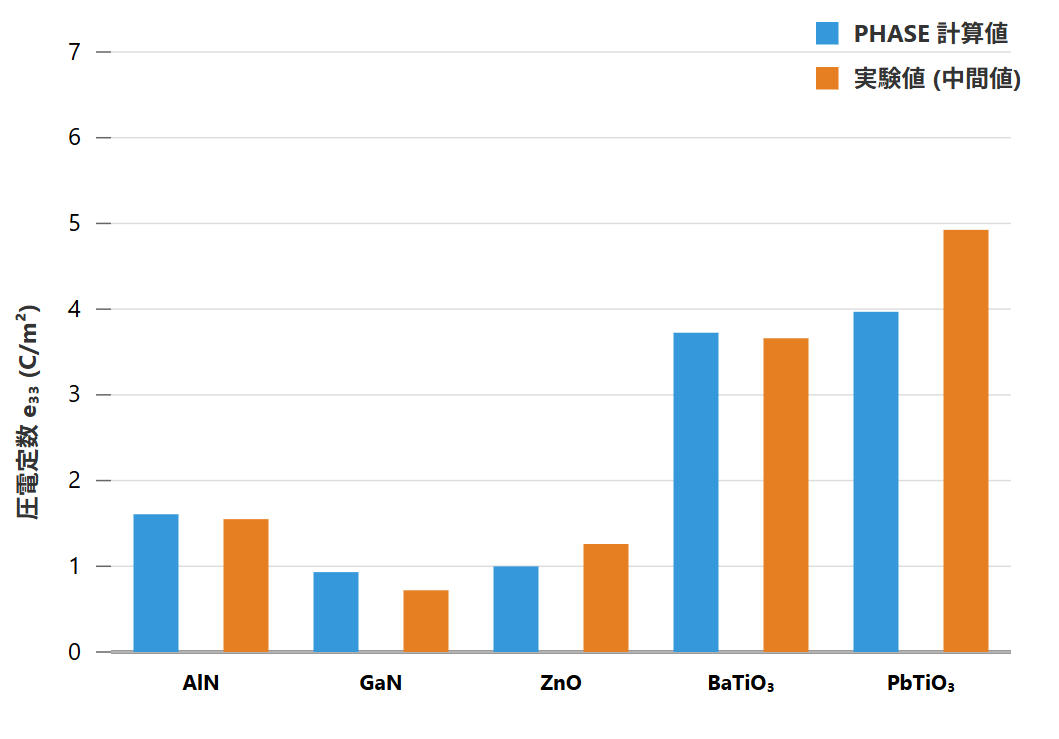
図2.　主要な圧電定数e₃₃の計算値と実験値の比較

まとめ#

本解析では、第一原理計算ソフトウェアAdvance/PHASEのワークフロー機能を用い、ウルツ鉱型からペロブスカイト型まで、多様な圧電材料の圧電定数を高精度に計算できることを示しました。従来は専門家でも多大な労力を要した複雑な計算手順の構築が、ワークフロー機能によって簡略化され、信頼性の高い計算にスムーズに着手できるようになります。これにより、新しいセンサーやアクチュエーターに向けた圧電材料の探索や、性能向上のための材料設計が一層加速されることが期待されます。

参考文献#

K. Tsubouchi, and N. Mikoshiba, IEEE Transactions on Sonics and Ultrasonics 32, 634 (1985).
O. Ambacher et al., J. Appl. Phys. 87, 334 (2000).
I. B. Kobiakov, Solid State Communications 35, 305 (1980).
和田剛、上辻靖智、槌谷和義、マートプロセス学会誌2016年5巻1号 p. 9-15.
G. Sághi-Szabó, R.E. Cohen, and H. Krakauer, Phys. Rev. Lett. 80, 4321(1998).