ワークフロー構築と高精度な材料物性予測：格子誘電率#

物質が電場に対してどう応答するかを示す「誘電率」は、コンデンサや半導体デバイスのゲート絶縁膜など、電子部品の性能を左右する重要な物理量です。静的な誘電率（ $\epsilon_0$ ）は、電場に対する電子の応答である電子誘電率（ $\epsilon_{el}$ ）と、原子（イオン）の格子振動による応答である格子誘電率（ $\epsilon_{lat}$ ）の和で表されます。特に格子誘電率は、ベリー位相計算とフォノン計算などを含む複雑な計算が必要であり、さらに遷移金属酸化物のような電子相関の強い材料や、複雑な磁気構造を持つ材料では、その計算は一層困難になります。本解析では、第一原理計算ソフトウェアAdvance/PHASEのワークフロー機能を活用し、この格子誘電率の計算手法を検証します。

Keywords: 第一原理計算, 格子誘電率, 静的誘電率, 遷移金属酸化物, 磁気構造

計算手法：複雑な材料へのアプローチ#

格子誘電率（ $\epsilon_{lat}$ ）の計算は、大きく分けて2つのステップで構成されます。

ベリー位相理論を用いて、原子の変位に対する分極の変化、すなわちボルン有効電荷（ $Z^*$ ）を計算します。
フォノン計算を行い、格子振動のモードと振動数を求めます。

これらを組み合わせることで、格子振動に起因する誘電率を算出します。この一連の多段階プロセスは、図１のようにAdvance/PHASEのワークフロー構築機能によって効率的に実現することができます。

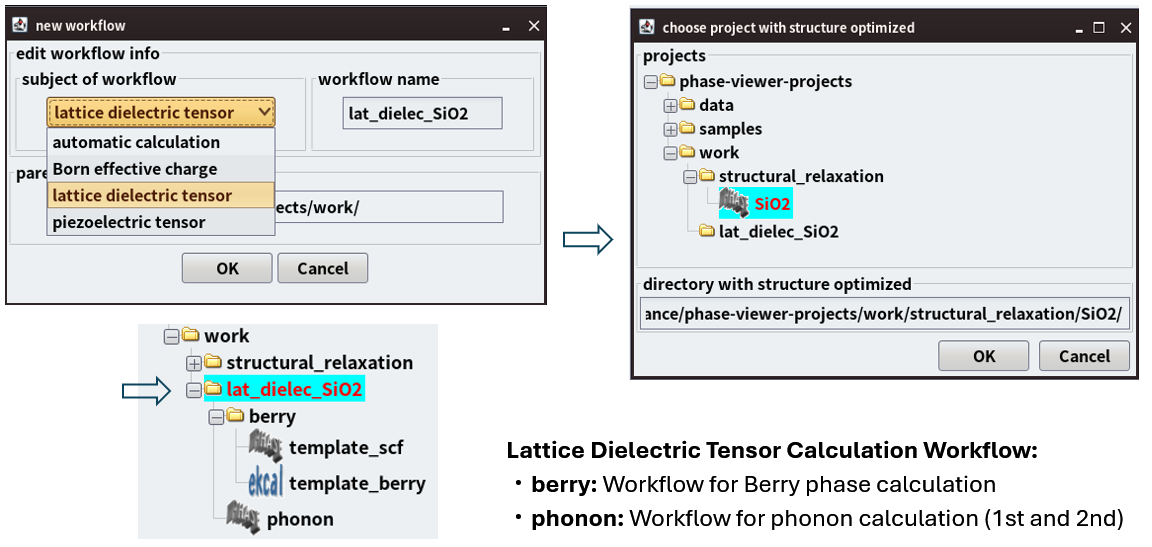
図1. GUIから「lattice dielectric tensor」を選択するだけで、格子誘電率の計算（ベリー位相計算とフォノン計算）のフローが自動的に構築されます。

また、本事例で扱う遷移金属酸化物では、d電子間の強いクーロン反発（電子相関）を記述するため、DFT+U法を用いています。Uの値は、バンドギャップなどの物理量を実験値とよく一致させるように決定されています[1]。

解析事例：複雑な磁性酸化物への応用#

反強磁性体 CoO#

酸化コバルト(CoO)は、低温で隣り合う(111)面の磁気モーメントが逆向きに整列する、AF-II型と呼ばれる複雑な反強磁性秩序を示すことが知られています(図2)。

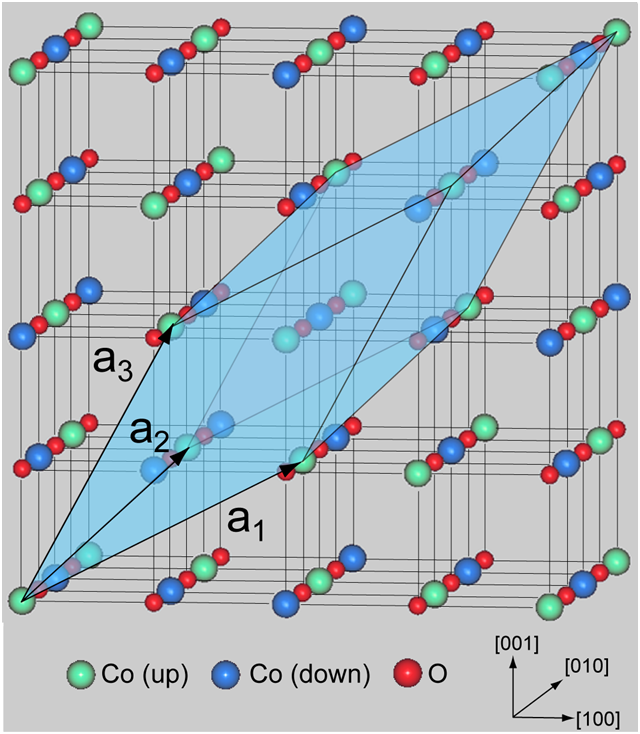
図2. CoOの結晶構造とAF-II型反強磁性秩序

この複雑な系に対し、U_eff = 4.5 eVとして計算した誘電率を表1に示します。電子誘電率と格子誘電率の和から求めた静的誘電率の計算値は、実験値 [2] とよい一致を示しています。

表1. CoOの静的誘電率（対角成分）の計算値と実験値の比較

電子誘電率 ( $\epsilon_{el}$ )	格子誘電率 ( $\epsilon_{lat}$ )	合計: 静的誘電率 ( $\epsilon_0$ )	実験値 [2]
6.86	3.59	10.45	10.9

リチウムイオン電池正極材料 (LiFePO₄, LiCoPO₄)#

オリビン構造を持つLiFePO₄やLiCoPO₄は、リチウムイオン電池の正極材料として注目されている物質です。これらの材料も、FeやCoサイトに局在した磁気モーメントが反強磁性的に配列しています。

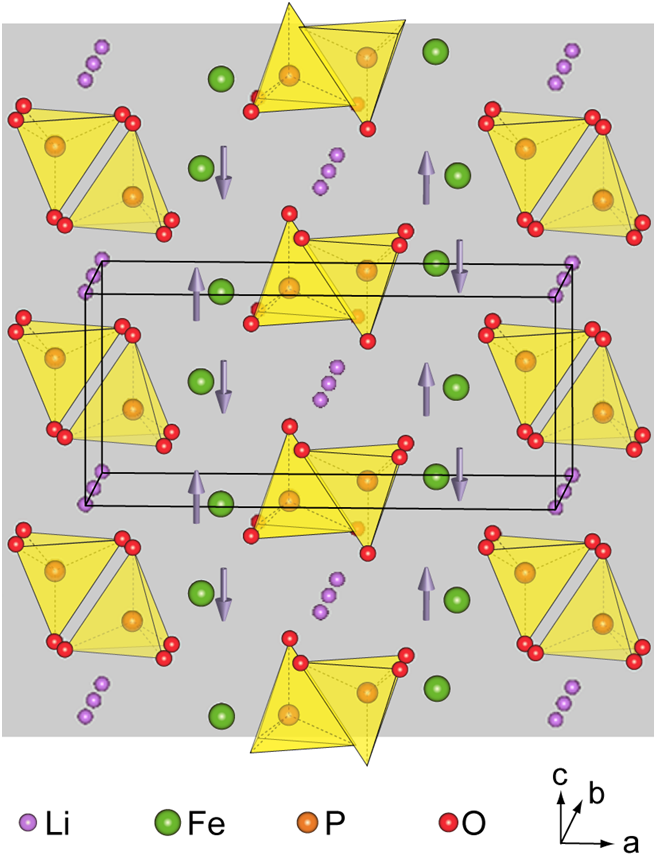
図3. LiFePO₄のオリビン構造

これらの材料の静的誘電率は、電池内での電場分布やイオンの移動しやすさに影響を与える重要なパラメータです。表2に、LiFePO₄とLiCoPO₄の静的誘電率テンソルの各成分を示します。計算結果から、両材料ともに結晶方位によって誘電率が異なる「異方性」を持つことがわかります。特にLiFePO₄はxx方向、LiCoPO₄はzz方向で分極しやすい特性を示します。

表2. オリビン型正極材料の誘電率テンソル（対角成分）の計算結果

物質 (U_eff)	成分	電子誘電率 (ε_el)	格子誘電率 (ε_lat)	静的誘電率 (ε₀)
LiFePO₄ (4.3 eV)	xx	5.82	2.95	8.77
	yy	5.70	2.51	8.21
	zz	5.64	2.37	8.01
LiCoPO₄ (4.0 eV)	xx	5.10	2.23	7.33
	yy	5.08	2.24	7.32
	zz	5.02	2.77	7.79

まとめ#

本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、複雑な磁気構造と強い電子相関を持つ遷移金属酸化物の格子誘電率を計算しました。反強磁性体CoOの計算では、静的誘電率が実験値とよく一致することを確認しました。また、リチウムイオン電池の正極材料であるLiFePO₄やLiCoPO₄についても、有用な計算結果が得られました。これらの結果は、本解析で用いたワークフロー機能が、複雑な材料系の格子誘電率といった物性計算に有効なアプローチであることを示しています。

参考文献#

T. Maxisch, F. Zhou, and G. Ceder, Physical Review B 73, 104301 (2006).
K. V. Rao and A. Smakula, Journal of Applied Physics 36, 2031 (1965).