Wannier局在軌道の解析・Wannier90連携による化学結合と電子状態の解釈#

PHASE logo

結晶の中の電子は、通常、波のように結晶全体に広がった「ブロッホ軌道」として記述されます。しかしこのままでは、化学で馴染みのある「原子間の結合」といった直感的なイメージを得ることは困難です。そこで、この広がった波を数学的に変換し、特定の原子サイト周辺に局在させた「ワニエ（Wannier）局在軌道」が有効な手法です。ワニエ軌道を用いることで、電子の分布、つまり化学結合の様子を直接的に可視化し、物質の分極などの性質を深く理解することができます。本稿では、第一原理計算ソフトウェアAdvance/PHASEの標準機能と、最大局在ワニエ関数計算プログラムWannier90との連携を用い、化学結合の可視化から、より高度な電子状態解析までを紹介します。

Keywords: 第一原理計算, Wannier局在軌道, Wannier90, 化学結合, 共有結合, イオン結合, バンド図, フェルミ面, ハミルトニアン, Si, GaAs, Graphite

第1部：ポスト処理によるWannier局在軌道の可視化#

Wannier局在軌道とは？#

一般に、ワニエ関数は一意には定まりませんが、「その「広がり」が最小になるように定めることで、物理的に意味のある一意な「最大局在ワニエ関数 (Maximally Localized Wannier Functions, MLWFs)」を得る手法が確立されています [1]。この関数の二乗は電子の分布を、中心位置は電子分布の平均位置を表します。なお、MLWFsの「一意性」は、解析対象とするバンド群（ヒルベルト部分空間）を固定した上でのものであり、どのバンドを選択するかによって得られるMLWFsは変わる点に注意が必要です。

MLWFsを用いることの利点は、量子力学に基づいた複雑な計算結果を、私たちに馴染み深い化学結合の描像として解釈する点にあります。純粋な共有結合と、少しイオン性を帯びた結合とでは、電子の分布にどのような違いが現れるのでしょうか。

計算結果：SiとGaAsにおける化学結合の比較#

図1に、計算されたSi結晶とGaAs結晶のMLWFs（の等値面）を示します。オレンジ色と青色の部分は、それぞれ波動関数の符号が正と負の領域を表しており、このペア全体で一つの化学結合に対応します。図には代表的なワニエ関数が一つだけ描かれていますが、これは視認性を良くするためです。実際の結晶では、全ての等価な化学結合の場所に、これと全く同じ形のワニエ関数が無数に存在します。

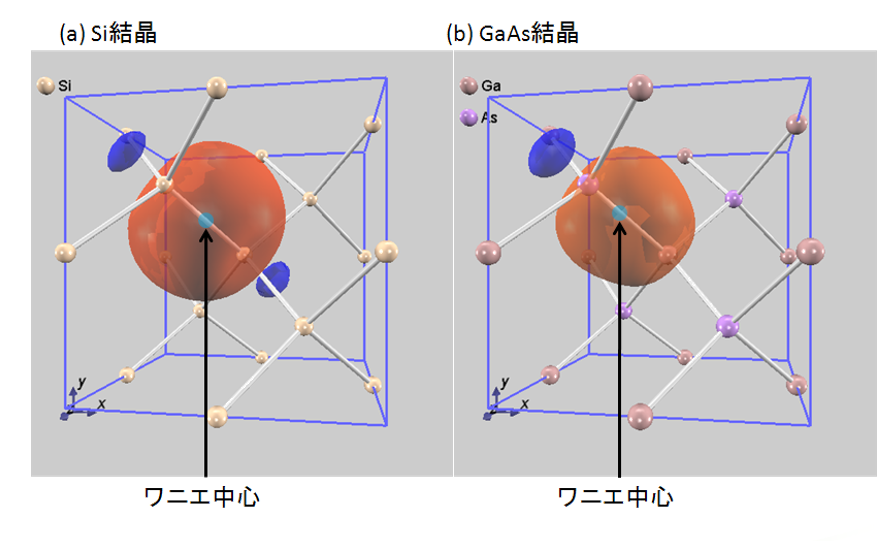
Wannier functions in Si and GaAs crystals

図1. (a) Si結晶と, (b) GaAs結晶におけるワニエ関数(MLWFs)。矢印は電子分布の中心である「ワニエ中心」の位置を示しています。

(a) Si結晶：理想的な「共有結合」の姿#

Si結晶では、同じSi原子同士が結合しています。図1(a)を見ると、ワニエ中心が二つのSi原子を結ぶ直線上のほぼ中央に位置していることがわかります。これは、結合に関わる電子がどちらの原子にも偏ることなく、公平に共有されていることを示しており、理想的な共有結合の描像と一致します。

(b) GaAs結晶：隠れた「イオン結合性」の可視化#

一方、GaAs結晶では、ガリウム(Ga)原子とヒ素(As)原子という異なる種類の原子が結合しています。図1(b)に示すように、ワニエ中心が結合の中央から、ヒ素(As)原子の側へずれている点が特徴的です。

これは、ヒ素の方がガリウムよりも電子を引きつける力（電気陰性度）が強いため、共有されている電子がヒ素側に引き寄せられていることを示唆します。つまり、GaAsの結合は、共有結合的な性質を持ちながらも、電荷の偏り（分極）を持った「イオン性を帯びた共有結合」であることが、このワニエ中心のシフトから示されています。このミクロな電荷の偏りが、物質全体の電気的な性質へと繋がっていきます。

SiとGaAsの解析結果は、文献 [1] の図2で示されているものと一致しており、MLWFsの化学結合解析への有用性を示す典型的な事例です。

第2部：Wannier90との連携による高度な電子状態解析#

Advance/PHASEでは、最大局在ワニエ関数を計算するプログラムであるWannier90 [2, 3] との連携機能を備えています。これにより、化学結合の可視化だけでなく、バンド構造の補間、フェルミ面の描画、タイトバインディングモデルのハミルトニアン構築など、より一歩進んだ解析が可能になります。

計算フロー#

Wannier90との連携は、第一原理計算で得られたブロッホ状態をWannier90に入力し、ワニエ関数を構築するという流れで実行されます。この連携には、対象とするバンドの選択や、物理的に意味のある局在軌道を得るためのパラメータ設定など、背景知識を要する部分があります。これらのインプット作成や実行、ポスト処理のプロセスを効率化することを目的としてGUIが開発されています。図2はWannier90連携機能の操作パネルのスナップショットを示しています。

Wannier90 integration GUI example

図2. GUIによるWannier90連携機能の操作パネル。インプット作成からポスト処理、可視化までを統合的に管理できます。

計算例：グラファイト(Graphite)の電子状態#

連携機能の計算例として、グラファイトの電子状態解析の結果を示します。グラファイトの伝導特性を支配するπバンドは、価電子帯の上部でσバンドとエネルギー的に交差（エンタングル）しています。このような場合、物理的に意味のあるp_z軌道由来のワニエ関数を得るために、適切な「初期射影軌道」（この場合は炭素原子サイトのp_z軌道）を指定し、「ディスエンタングルメント」処理を用いて目的のバンド成分を抽出する手続きが必要となります。これらの設定を適切に行うことで、ワニエ関数の3D表示、精密なバンド図、逆格子空間での等エネルギー面が描画できます（図3）。

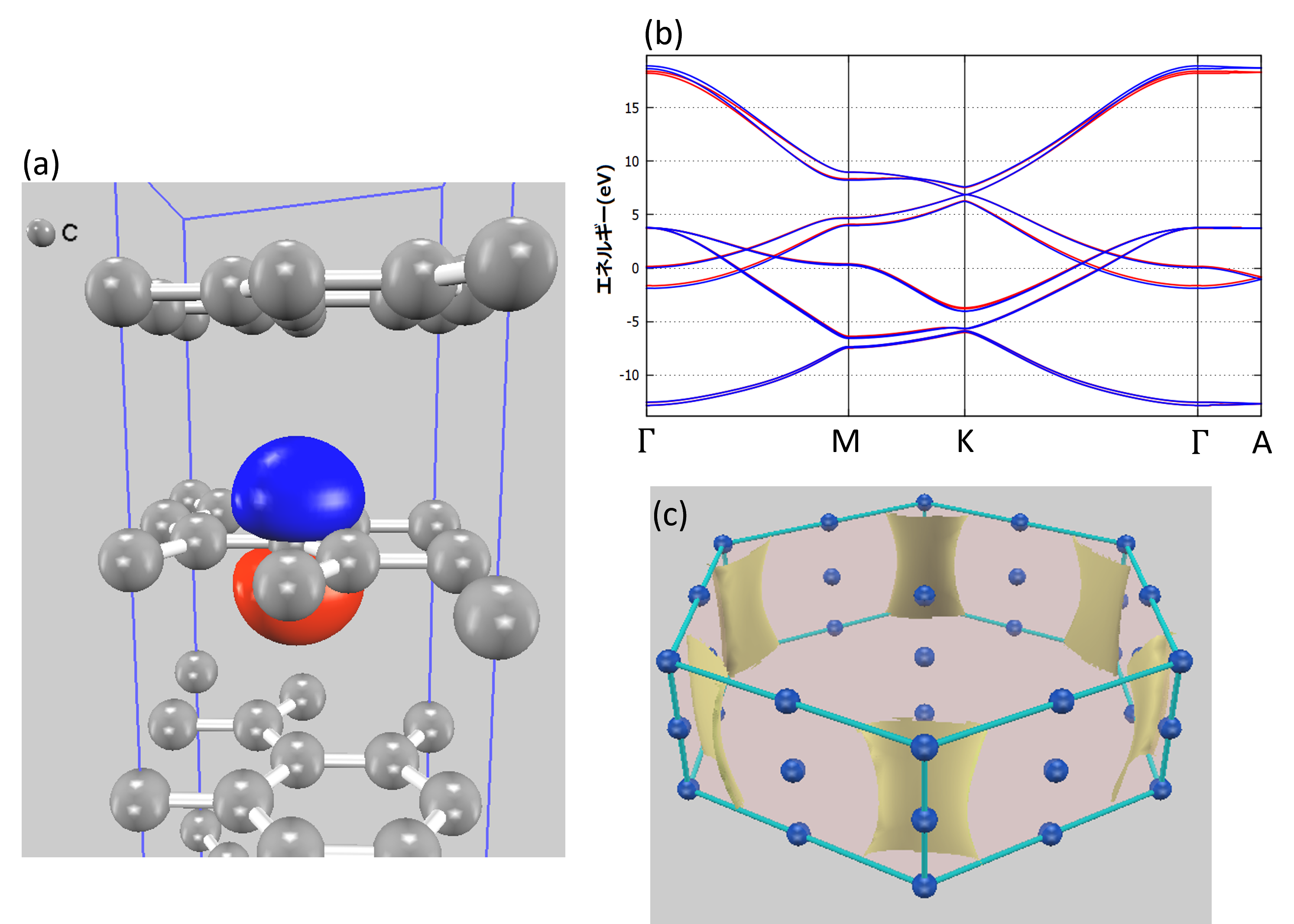
Analysis results for graphite using Wannier90 integration

図3. Wannier90連携によるグラファイトの解析結果。(a) p_z軌道由来のワニエ関数, (b) バンド図 (赤線：Advance/PHASEとWannier90による結果、青線：別の計算コード（Quantum ESPRESSO）とWannier90による結果との比較), (c) 逆空間での等エネルギー面。

グラファイトのp_z軌道の重要性#

図3(a)で可視化されたワニエ関数は、炭素原子のp_z軌道に相当し、グラファイトの特異な性質を理解する上で極めて重要です。この軌道は、炭素原子が蜂の巣状に結合したグラフェン平面に対して垂直な方向を向いています。隣り合う炭素原子のp_z軌道同士がゆるやかに重なり合うことでπ（パイ）結合を形成します。このπ結合の電子は特定の原子間に縛られず、シート全体を自由に動き回ることができるため（非局在化）、グラファイトは金属のような非常に高い電気伝導性を示します。このように、ワニエ関数は、ミクロな電子軌道がどのようにして物質のマクロな性質に結びついているのかを解釈する助けとなります。

また、図3(b)でAdvance/PHASEを用いた計算が、ベンチマークとして利用されるQuantum ESPRESSOによる結果と非常によく一致していることを示しており、本手法の計算精度の高さを裏付けています。

ハミルトニアンの構築と可視化#

Wannier90連携の応用の一つが、タイトバインディングモデルのハミルトニアンを構築し、その要素を可視化することです。

ハミルトニアンの式とその意味#

ここで構築されるハミルトニアンは、結晶中の電子の振る舞いを記述する「タイトバインディングモデル」のもので、以下の式で表されます。 $H = \sum_{\mathbf{R}, \mathbf{R'}} \sum_{\alpha, \beta} t_{\alpha \beta}(\mathbf{R} - \mathbf{R'}) c^\dagger_{\mathbf{R}\alpha} c_{\mathbf{R'}\beta}$ この式は「結晶中のあらゆる電子の飛び移りパターンのエネルギーを全部足し合わせたもの」と解釈できます。各記号は以下のような意味を持っています。

$H$ : 電子系全体の総エネルギー。
$c^\dagger_{\mathbf{R}\alpha} c_{\mathbf{R'}\beta}$ : 電子が格子サイト $\mathbf{R'}$ の軌道 $\beta$ から、格子サイト $\mathbf{R}$ の軌道 $\alpha$ へ「飛び移る（ホッピングする）」という操作を表します。
$t_{\alpha \beta}(\mathbf{R} - \mathbf{R'})$ : 2つの軌道間の電子の「飛び移りやすさ」を表すホッピング積分です。この値は軌道の種類 $\alpha, \beta$ と、サイト間の相対位置ベクトル $\mathbf{R} - \mathbf{R'}$ にのみ依存します。この値の絶対値が大きいほど、電子はその軌道間を活発に移動できることを意味します。

ヒストグラムの解釈#

図4の3Dヒストグラムは、この式の最も重要なパラメータであるホッピング積分 $t$ の値をプロットしたものです。X軸(β)とY軸(α)はワニエ関数のインデックスに対応します。（例えば、グラファイトの単位胞には2つの炭素原子が含まれるため、インデックス1が原子Aのp_z軌道、インデックス2が原子Bのp_z軌道、といった具体的な対応付けを考えることができます。）高さがホッピング積分の大きさを示します。

ヒストグラムに付記されている $\mathbf{R}$ は、電子が飛び移る二つの原子サイト間の相対位置ベクトル（ここでは $\mathbf{R} - \mathbf{R'}$ に相当）を表しています。

図4(a) $\mathbf{R}=(0,0,0)$ : これは、二つの軌道が同じ原子サイト上にある場合（オンサイト）の相互作用（オンサイトエネルギー）を示します。
図4(b) $\mathbf{R}=(1,0,0)$ : これは、ある原子と、そこから格子ベクトル一つ分だけ離れた隣接サイトの原子との間の相互作用を示します。

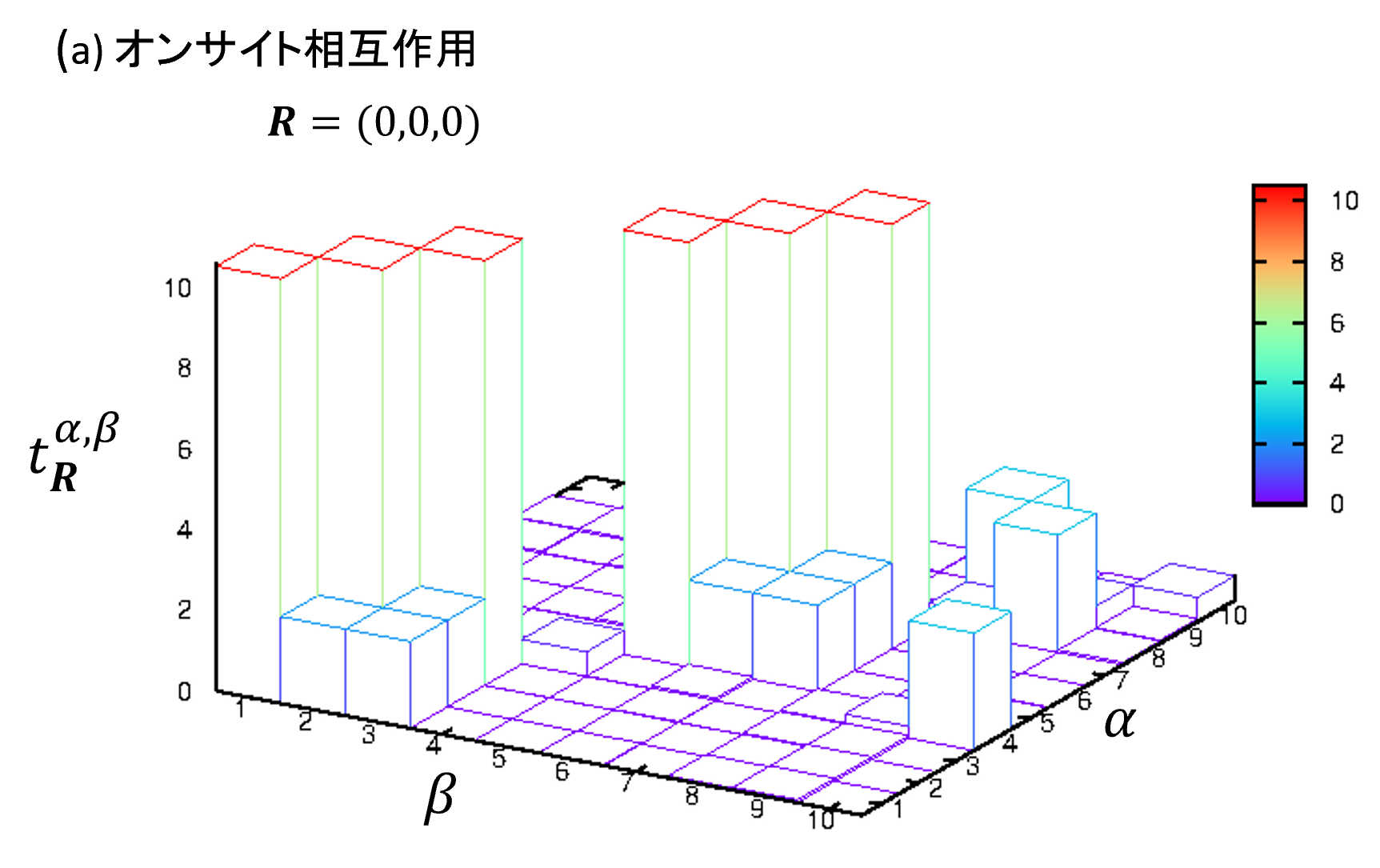
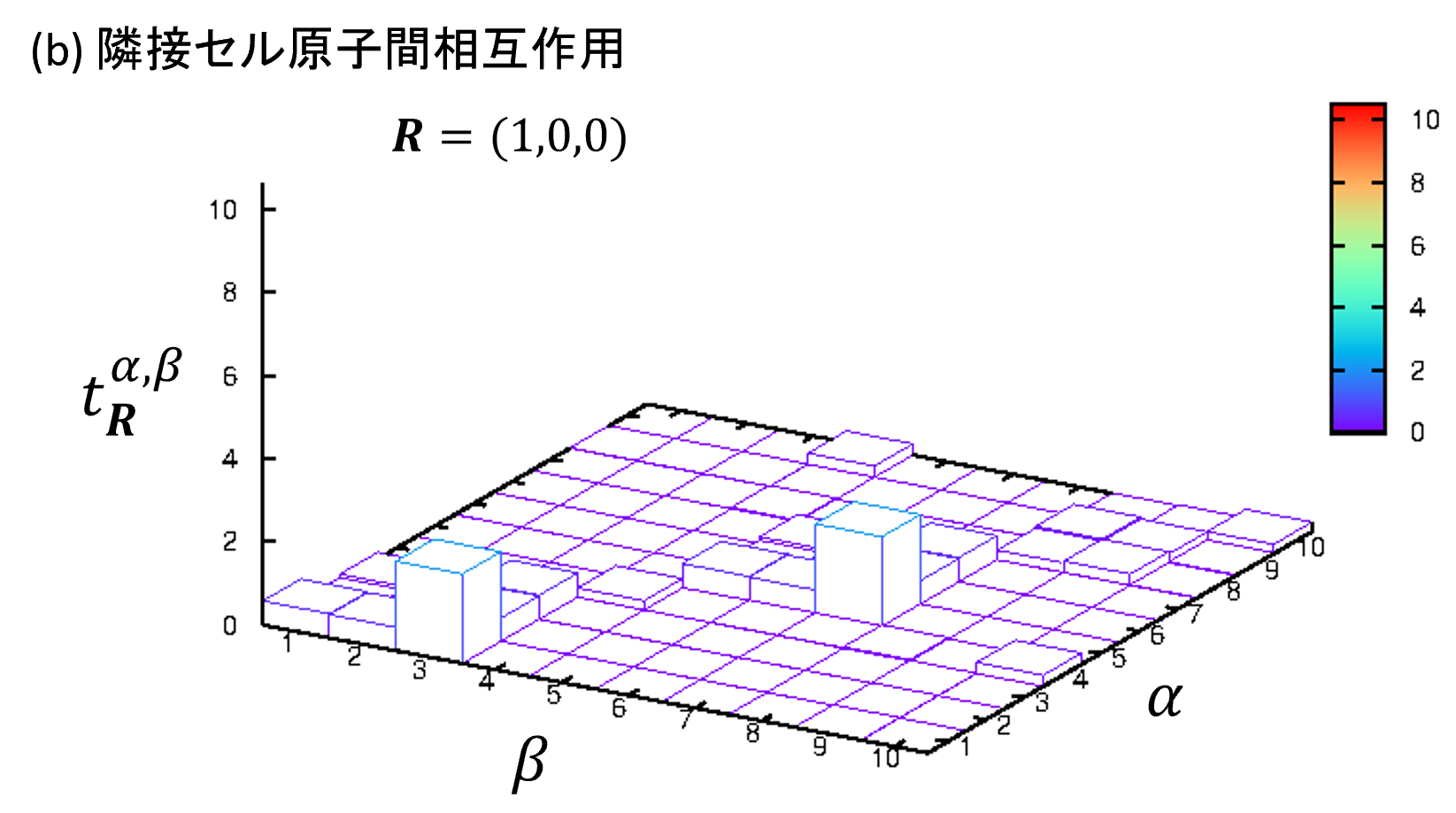
3D histogram visualization of Hamiltonian elements

図4. ハミルトニアンの要素を3次元ヒストグラムで可視化した例。X軸とY軸がワニエ関数のインデックスのペア、高さがホッピング積分 $t$ の大きさに対応します。異なるプロットは異なる相対位置ベクトル $\mathbf{R}$ での相互作用を示しており、 $\mathbf{R}$ が大きくなる（原子間距離が離れる）につれて相互作用（棒の高さ）が急激に小さくなっていく様子が分かります。

この可視化により、「どの原子とどの原子の間で、どの軌道同士の相互作用が強いのか」が定量的に評価できます。これにより、物性モデルを構築する際に、どの相互作用までを考慮に入れるべきかといった重要な判断を、視覚的な情報に基づいて行うことができます。

まとめ#

本解析事例では、第一原理計算ソフトウェアAdvance/PHASEが持つ機能とWannier90との連携による電子状態解析を紹介しました。標準機能によるワニエ軌道解析では、SiやGaAsの例で示したように、化学結合の様式（共有結合性、イオン性）を直感的に理解することができます。さらに、Wannier90とのGUI連携機能を用いれば、グラファイトの例で示したように、バンド図やフェルミ面の精密な描画から、タイトバインディングモデルのハミルトニアン要素の可視化まで、より高度で専門的な電子状態解析が可能になります。これらの機能により、複雑な第一原理計算の結果と、物理的・化学的な直感やモデル構築とを結びつけ、物質の性質をより深く多角的に理解することが可能になります。本稿で示したSiやグラファイトは、ワニエ局在軌道の概念を理解する上で理想的な系です。実際の研究で対象となる、より複雑なバンド構造を持つ材料（例えば、d電子やf電子が絡む遷移金属酸化物など）では、本稿でも触れた適切な初期射影やディスエンタングルメント処理が解析の鍵となります。

参考文献#

N. Marzari, A. A. Mostofi, J. R. Yates, I. Souza, and D. Vanderbilt, "Maximally localized Wannier functions: Theory and applications", Rev. Mod. Phys. 84, 1419 (2012).
G. Pizzi, V. Vitale, R. Arita, S. Blügel, F. Freimuth, G. Géranton, M. Gibertini, D. Gresch, C. Johnson, T.Koretsune, J. Ibañez-Azpiroz, H. Lee, J. M. Lihm, D. Marchand, A. Marrazzo, Y. Mokrousov, J. I. Mustafa, Y. Nohara, Y. Nomura, L. Paulatto, S. Poncé, T. Ponweiser, J. Qiao, F. Thöle, S. S. Tsirkin, M. Wierzbowska, N. Marzari, D. Vanderbilt, I. Souza, A. A. Mostofi, and J. R. Yates, "Wannier90 as a community code: new features and applications", J. Phys. Cond. Matt. 32, 165902 (2020).
https://wannier.org/