第一原理計算による結晶の格子振動解析#

結晶中の原子は静止しているわけではなく、格子点を中心に絶えず振動しています。この集団的な原子の振動は量子化され、「フォノン」または「格子振動」と呼ばれます。フォノンは、熱伝導、比熱、熱膨張、電気抵抗といった物質の基本的な熱力学的・電気的特性を支配するだけでなく、ラマン散乱や赤外吸収などの分光学的応答、さらには超伝導や誘電性といった機能性の発現にも深く関わっています。したがって、物質の性質を微視的なレベルから理解し、新しい機能性材料を設計するためには、格子振動の状態、すなわちフォノンの振動数や振動モードを正確に知ることが不可欠です。ここでは、第一原理計算ソフトウェアAdvance/PHASEを用いて様々な物質の格子振動解析を行います。その計算結果が、既知の実験値とどのように対応するかを比較・議論することで、計算の妥当性を示します。
Keywords: 第一原理計算, DFTシミュレーション, 格子振動, フォノン, 結晶の対称性, ラマン分光, 赤外分光
計算手法#
本解析における格子振動計算は、一般に有限変位法(Frozen Phonon法)として知られています。具体的には、原子に微小な変位を与えた際に各原子に働く力(原子間力)を精密に計算し、その結果から力の定数行列(ヘシアン)を構築します。この行列を対角化することで、系の基準振動モードとその振動数(フォノン周波数)を求めます。Advance/PHASEでは、結晶の対称性を活用することで、計算対象の変位パターンを最小限に抑え、高精度な結果を効率的に得ることが可能となっています。なお、本解析は交換相関汎関数としてGGA-PBEを使用します。また、本計算で採用している有限変位法では、赤外活性なモードで生じるLO-TO分裂(縦波光学-横波光学モード分裂)は考慮されません。そのため、得られる計算値は横波光学(TO)モードの振動数に対応します。
予備知識:剛体運動と虚数振動数
フォノン解析の結果を正しく理解するために、「振動数ゼロのモード」と「虚数振動数」について解説します。これらは計算が正しく行われたか、また対象とする結晶構造が安定に存在できるかを判断する上で重要な指標です。
1. ゼロ振動数モード(音響モード)#
フォノンの計算において、波数がゼロ(Γ点)の振動を考えるとき、特定のモードの振動数がゼロになります。これは原子間に復元力が働かない、系全体が一斉に動く「剛体運動」に対応します。この扱いは、対象が周期的な「結晶」か、孤立した「分子」かで異なります。
結晶の場合#
- 3つの並進モード(音響モード): 結晶全体がx, y, z軸方向に平行移動する動きです。これは音波の伝わりに相当し、Γ点では振動数がゼロになります。
- 回転モードについて: 周期的な結晶では、系全体が一体となって回転する剛体回転モードは存在しません。
孤立分子の場合(参考)#
- 分子単体の振動計算では、並進運動に加えて回転運動も考慮します。N個の原子からなる非直線分子では、3つの並進モードと3つの回転モードの合計6個のモードがゼロ振動数となります。
2. 虚数振動数と構造安定性#
計算結果に虚数の振動数(出力ファイル上では負の値で表示されることが多い)が現れた場合、それはその構造が動的に不安定であることを示します。
-
物理的な意味(構造不安定性): 虚数振動数は、構造がポテンシャルエネルギーの極小点(安定点)ではないことを示します。特に、もし大きな虚数振動数が1つだけ現れた場合、その構造は構造変化の経路における遷移状態(鞍点)にあることを強く示唆します。そのモードは、より安定な構造へ向かうための「道筋」を示しており、構造探索において極めて重要な情報となります。
-
計算上の注意点: 物理的な不安定性とは別に、計算上の理由で小さな虚数が現れることがあります。
- 音響モードのノイズ: 本来ゼロになるはずの3つの音響モードが、数値誤差によりゼロに近い小さな虚数として現れることがあります。これは計算上のノイズであり、無視すべきものです。
- 不完全な構造最適化: 構造最適化がエネルギーの谷底に完全に到達していない場合にも、音響モード以外のモードで小さな虚数が現れることがあります。これは構造が真の安定点に「ごくわずかに届いていない」ことを示唆しており、より厳しい条件で構造を再最適化することで解消される場合があります。 したがって、結晶の振動解析を行う際には、Γ点に現れる3つの音響モード(計算上はわずかな虚数を含む場合がある)を予め除外して考えることが重要です。本解析で示すグラフも、これらの音響モードを除いた、真の内部振動(光学モード)のみを表示しています。
計算結果と考察#
ウルツ鉱型結晶GaN: 多様な対称性モード#
窒化ガリウム(GaN)は、ウルツ鉱型の六方晶構造をとる重要な半導体材料です。そのΓ点における光学モードは、結晶の対称性から, , , の4種類に分類されます。
表1は本計算で得られた各モードの振動数(計算値)を示します。図1は計算値とラマン・赤外分光実験による測定値(実験値)[1] の比較を示します。例えば、ラマン活性なモードの計算値は136 cm-1および547 cm-1となり、実験値の約144 cm-1、569 cm-1に対応します。
計算値が実験値に対しておおむね良好な一致を示していますが、全体的にやや低い値を示す傾向が見られます。これは計算に用いた交換相関汎関数GGAが、一般にフォノン周波数を数%程度、過小評価する傾向があるためです。
また、表1で「Silent (NON)」と表記されているモード(計算値 314, 645 cm-1)に注目します。このモードは、対称性の観点からの選択律により、ラマン散乱と赤外吸収のいずれに対しても不活性(非活性)です。そのため、光学的な実験手法では原理的に観測されず、図1においても対応する実験値(点線)は存在しません。第一原理計算は、このような光学的に観測できないサイレントモードの振動数を予測できるという利点も持ちます。
表1. GaNの振動モードデータ(計算値)
| 対称性 | 活性 | 振動数 (cm-1) |
|---|---|---|
| E2 | R | 136, 547 |
| B1 | Silent (NON) | 314, 645 |
| A1 | IR&R | 490 |
| E1 | IR&R | 540 |
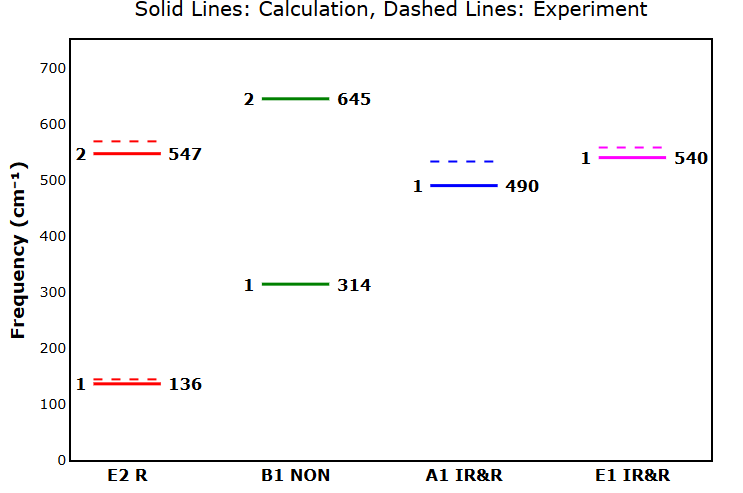
図1. ウルツ鉱型GaNのΓ点における振動モード(実線:計算値、点線:実験値)
SiO2 (石英)#
石英(SiO2)はGaNより単位胞あたりの原子数が比較的多いため、多くの振動モードを示します。計算結果は実験の特徴をよく捉えています。例えば、石英のフォノンで最も代表的なラマン活性なモードは、実験では466 cm-1に強いピークとして観測されますが [2]、これに対する計算値は445 cm-1とよく対応します。他の多数のモードについても図2が示すように、計算値は実験値に対してやや低い振動数を与える傾向にありますが、これはGGA計算の一般的な特徴と一致しており、全体として実験スペクトルのパターンを再現しています [2, 3]。
表2. SiO2の振動モードデータ(計算値)
| 対称性 | 活性 | 振動数 (cm-1) |
|---|---|---|
| E | IR&R | 139, 258, 371, 428, 663, 761, 1002, 1091 |
| A1 | R | 226, 333, 445, 1021 |
| A2 | IR | 334, 477, 735, 1014 |
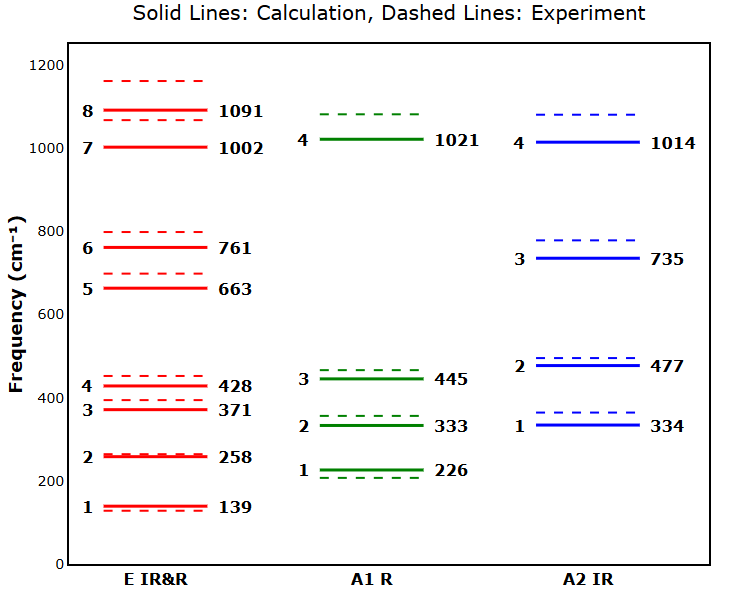
図2. α-SiO2のΓ点における振動モード(実線:計算値、点線:実験値)
LiTaO3 (タンタル酸リチウム)#
LiTaO3も多数の光学モードを持つ材料です。ラマンおよび赤外活性なモードやモードにおいて、計算値は実験値 [4] と妥当な対応を示しています(例:モードの計算値558 cm-1に対する実験値約600 cm-1)。ここでも計算値が実験値をやや下回る傾向が見られますが、全体的に良好な一致を示しています。一方で、モードは対称性選択律からラマン・赤外ともに不活性(Silent)です。そのため図3が示すように光学実験では観測されず、対応する実験値が存在しません。本計算手法は、こうしたサイレントモードも含めて包括的にフォノン状態を明らかにできる点が強みです。
表3. LiTaO3の振動モードデータ(計算値)
| 対称性 | 活性 | 振動数 (cm-1) |
|---|---|---|
| E | IR&R | 137, 197, 249, 305, 363, 377, 444, 558, 631 |
| A2 | Silent (NON) | 171, 278, 383, 441, 872 |
| A1 | IR&R | 192, 246, 364, 558 |
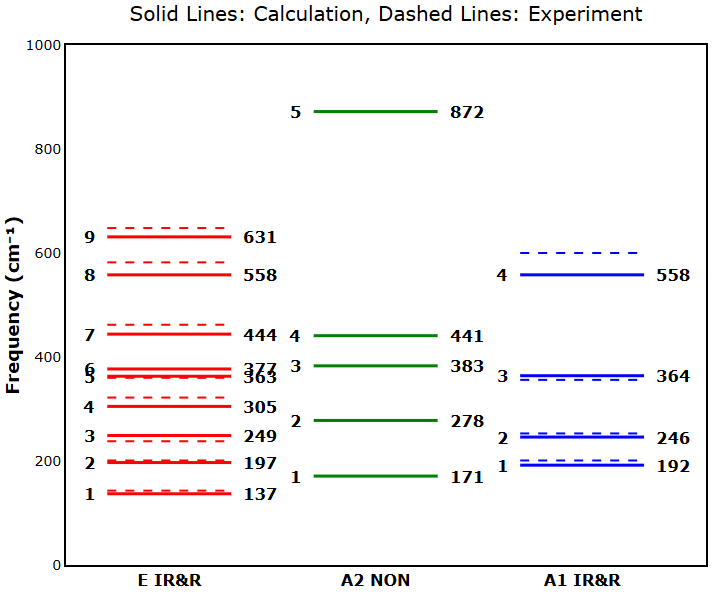
図3. 三方晶LiTaO3のΓ点における振動モード(実線:計算値、点線:実験値)
CaCO3 (方解石)#
方解石(CaCO3)の計算結果は、実験値 [5] と比較的良好な一致を示します。特に、低振動数側のラマン活性なモードでは、計算値156 cm-1と実験値157 cm-1が非常によく一致しています。最も強度の高いモード(計算値1055 cm-1 / 実験値1088 cm-1)も、GGA計算で一般的に見られるわずかな過小評価の妥当な範囲内で、実験値と良好な一致を示しています。また、本物質のフォノンモードには光学的に不活性なモードとモードが含まれます。これらはサイレントモードであるため、図4が示す通り、ラマンや赤外分光実験では観測されません。
表4. CaCO3の振動モードデータ(計算値)
| 対称性 | 活性 | 計算値 (cm-1) |
|---|---|---|
| A1g | R | 1055 |
| A2g | Silent (NON) | 164, 328, 820 |
| A1u | Silent (NON) | 292, 1055 |
| Eg | R | 156, 291, 680, 1397 |
| Eu | IR | 91, 233, 317, 681, 1363 |
| A2u | IR | 72, 331, 815 |
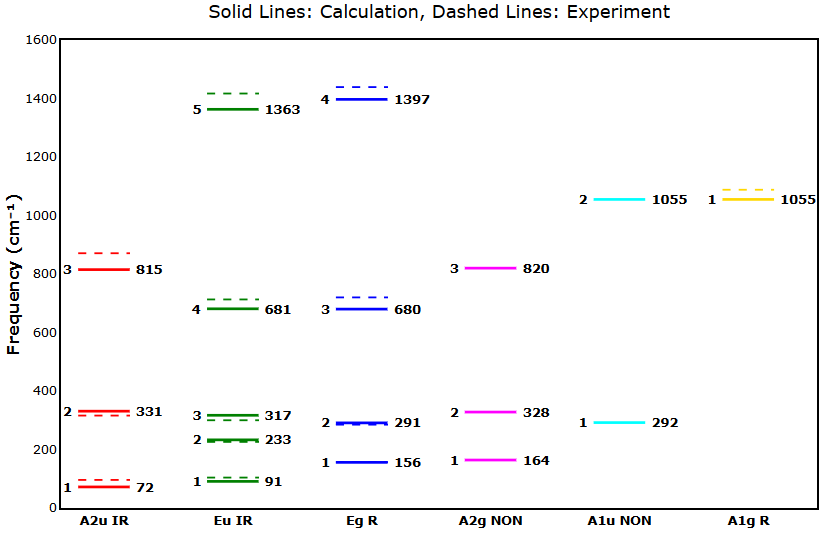
図4. 方解石(CaCO3)のΓ点における振動モード(実線:計算値、点線:実験値)
まとめ#
本解析では、第一原理計算ソフトウェアAdvance/PHASEを用いて、様々な結晶材料の格子振動(フォノン)をシミュレーションしました。その結果、得られた計算値は既知の実験データと良い一致を示し、本計算手法の妥当性を確認できました。GaN、SiO2、LiTaO3、CaCO3といった異なる対称性や構成原子を持つ系において、それぞれの振動モードを網羅的に決定できることを実証し、本手法の汎用性を示しました。
本解析の詳細や、研究への適用可能性に関するご相談はこちら
お問い合わせ参考文献#
- T. Azuhata, T. Matsunaga, K. Shimada, K. Yoshida, T. Sota, K. Suzuki, and S. Nakamura, "Optical phonons in GaN", Physica B: Condensed Matter 219, 493 (1996).
- S. M. Shapiro, D. C. O'Shea, and H. Z. Cummins, "Raman Scattering Study of the Alpha-Beta Phase Transition in Quartz," Phys. Rev. Lett. 19, 361 (1967).
- W. G. Spitzer and D. A. Kleinman, "Infrared Lattice Bands of Quartz", Phys. Rev. 121, 1324 (1961).
- W. D. Johnston, Jr. and I. P. Kaminow, "Temperature Dependence of Raman and Rayleigh Scattering in LiNbO3 and LiTaO3", Phys. Rev. 168, 1045 (1968).
- 工藤恵栄、光物性基礎、オーム社 (1996).
関連ページ#
- 第一原理計算ソフトウェア Advance/PHASE
- 解析分野:ナノ・バイオ
- 産業分野:材料・化学