フォノン解析による熱的特性の計算#

Advance/PHASE logo

固体の比熱や自由エネルギー、エントロピーといった熱的特性は、原子の集団的な振動である格子振動（フォノン）に大きく依存します。これらの物性値を正確に予測することは、半導体デバイスの熱設計や材料の相安定性評価など、幅広い分野で不可欠です。本解析事例では、第一原理計算ソフトウェアAdvance/PHASEを用い、半導体材料として広く利用されるシリコン（Si）を対象に、フォノン解析から熱的特性を算出する一連のプロセスと結果を紹介します。

Keywords: 第一原理計算, フォノン, 格子振動, 熱的特性, フォノン状態密度, 有限変位法

計算手法#

フォノン解析による熱的特性の計算は、調和近似に基づき、以下のステップで実行されます。

1. 構造最適化#

フォノン計算の基礎となる原子間の力定数は、原子が平衡位置から微小に変位した際の力の応答として定義されます。そのため、計算の起点となる原子の平衡位置を可能な限り正確に決定することが極めて重要です。本解析では、まずSiの単位格子に対して第一原理計算を行い、格子定数と原子位置を精密に最適化します。実験値やデータベースの構造をそのまま使うのではなく、設定された計算条件で最も安定な構造を求めることが、後続の計算精度を保証します。この際、エネルギーや力の収束基準を通常よりも厳しく設定することが望ましいです。

2. フォノン状態密度の計算#

次に、最適化された構造からフォノン計算用のプロジェクトを生成します。本解析では、力定数の計算に有限変位法を用います。この手法では、原子間相互作用を十分に考慮できる大きさのスーパーセルモデルを作成し、各原子を平衡位置から微小に変位させ（例：0.05 bohr）、その際に各原子に働く力を第一原理計算で求めます。これらの力と変位の関係から力定数行列を構築し、対角化することで、指定した波数（q点）メッシュにおける全てのフォノンモードの振動数を得ます。
得られた全モードの振動数分布をヒストグラム化したものがフォノン状態密度です。フォノン状態密度は、特定の振動数を持つ格子振動がどれだけ存在するかを表しており、熱的特性を計算するための基礎となります。

3. 熱的特性の算出#

フォノン状態密度 $g(\omega)$ が得られると、統計力学に基づいて様々な熱的特性を算出できます。これは、各振動数 $\omega$ を持つモードの寄与を、そのモード数である $g(\omega)$ で重み付けして全振動数範囲で積分することで計算されます。Advance/PHASEでは、フォノン計算後にGUIのスクリプト実行機能を用いて、これらの物性を容易に計算できます。主要な熱力学量は以下の式で与えられます [1]。

振動自由エネルギー (F): 材料の熱力学的な安定性を示す自由エネルギーにおいて、格子振動による寄与（零点エネルギーと温度依存項）です。

$$F(T) = \int_0^\infty g(\omega) \left[ \frac{1}{2}\hbar\omega + k_B T \ln\left(1 - e^{-\frac{\hbar\omega}{k_B T}}\right) \right] d\omega$$

定積熱容量 ( $C_V$ ): 材料がどれだけ熱を蓄えることができるかを示す指標です。

$$C_V(T) = \int_0^\infty g(\omega) k_B \left(\frac{\hbar\omega}{k_B T}\right)^2 \frac{e^{\frac{\hbar\omega}{k_B T}}}{\left(e^{\frac{\hbar\omega}{k_B T}} - 1\right)^2} d\omega$$

エントロピー (S): 系の乱雑さを表す熱力学量です。

$$S(T) = \int_0^\infty g(\omega) k_B \left[ \frac{\hbar\omega/k_B T}{e^{\hbar\omega/k_B T} - 1} - \ln\left(1 - e^{-\frac{\hbar\omega}{k_B T}}\right) \right] d\omega$$

ここで、各変数は以下の通りです。

$T$ : 絶対温度
$g(\omega)$ : フォノン状態密度
$\omega$ : フォノンの角振動数
$\hbar$ : ディラック定数（プランク定数 $h$ を $2\pi$ で割ったもの）
$k_B$ : ボルツマン定数

計算結果と考察#

Siのフォノン状態密度#

図1に、本手法で計算されたSiのフォノン状態密度を示します。横軸は振動数（単位: cm^-1）、縦軸は状態密度を表します。本計算で得られたフォノン状態密度は、格子振動の理論モデルとして広く知られるWeberの断熱ボンドチャージモデル（BCM）による計算結果 [2]と良好な一致を示し、主要な特徴が正確に再現されています。

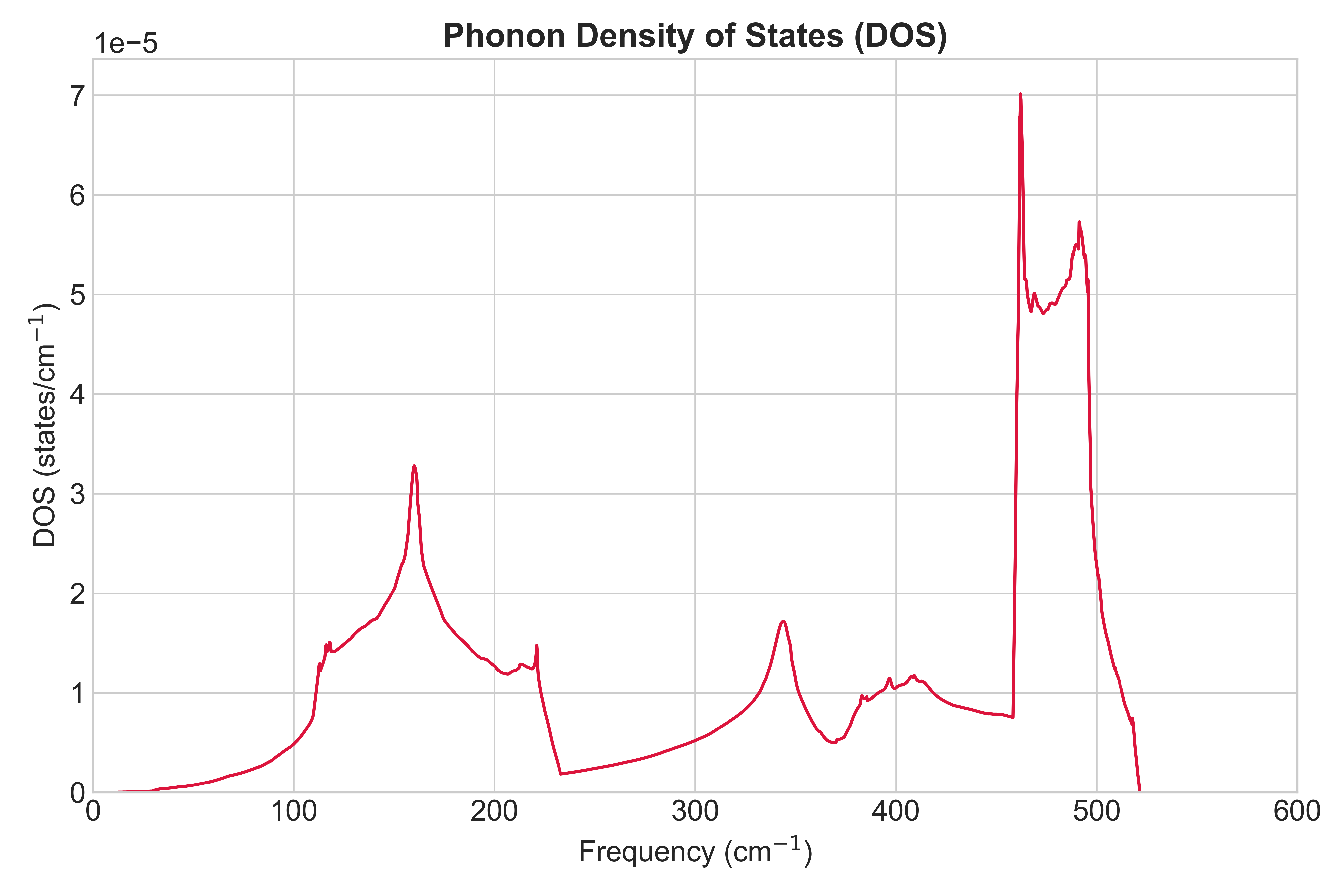
図1.　Siのフォノン状態密度

Siの熱的特性#

図1のフォノン状態密度を用いて計算した、Siの熱的特性の温度依存性を図2および図3に示します。

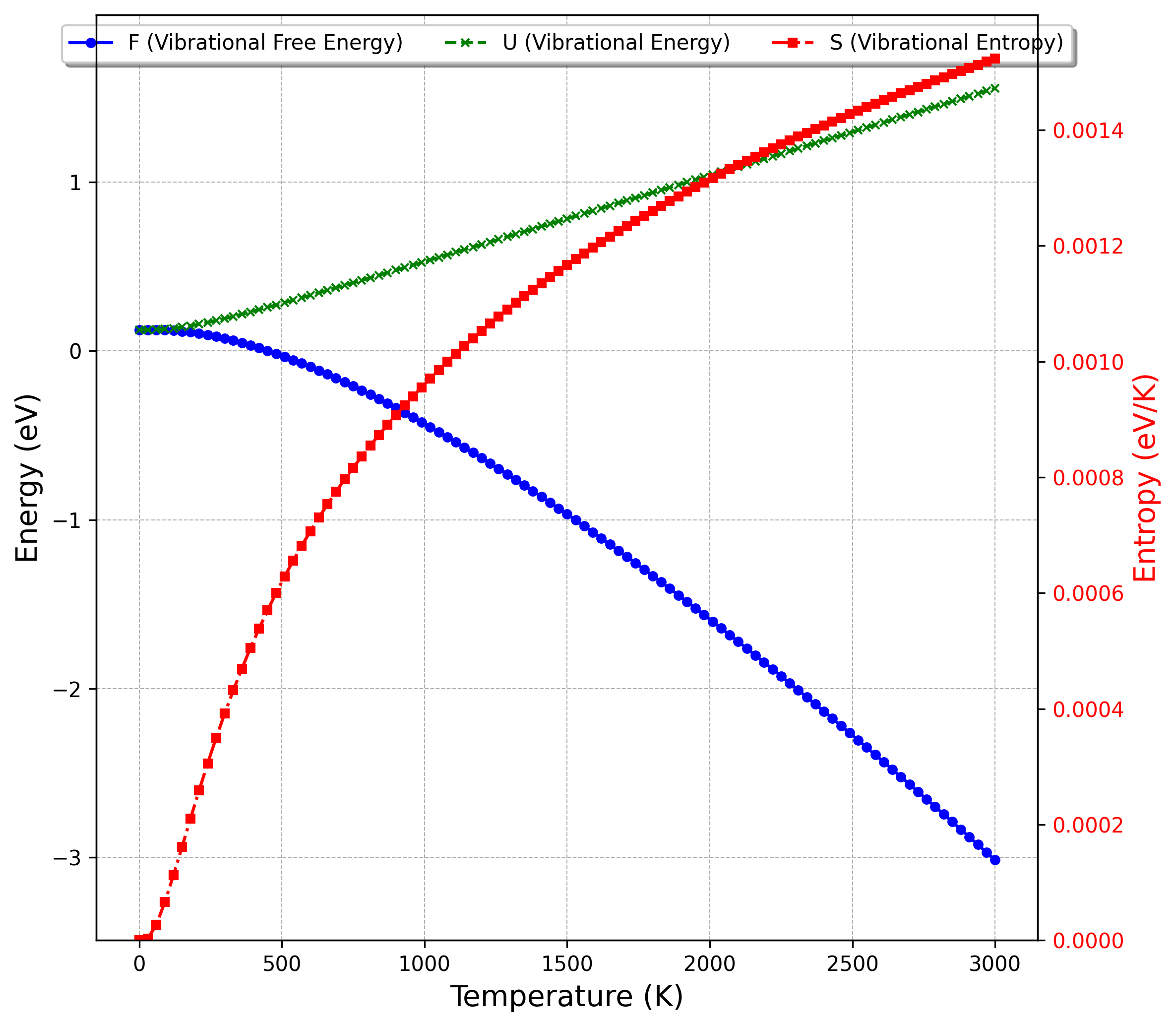
Siの振動自由エネルギー、内部エネルギー、エントロピーの温度依存性
図2.　格子振動に由来する自由エネルギー( $F$ )、内部エネルギー( $U$ )、エントロピー( $S$ )の温度依存性

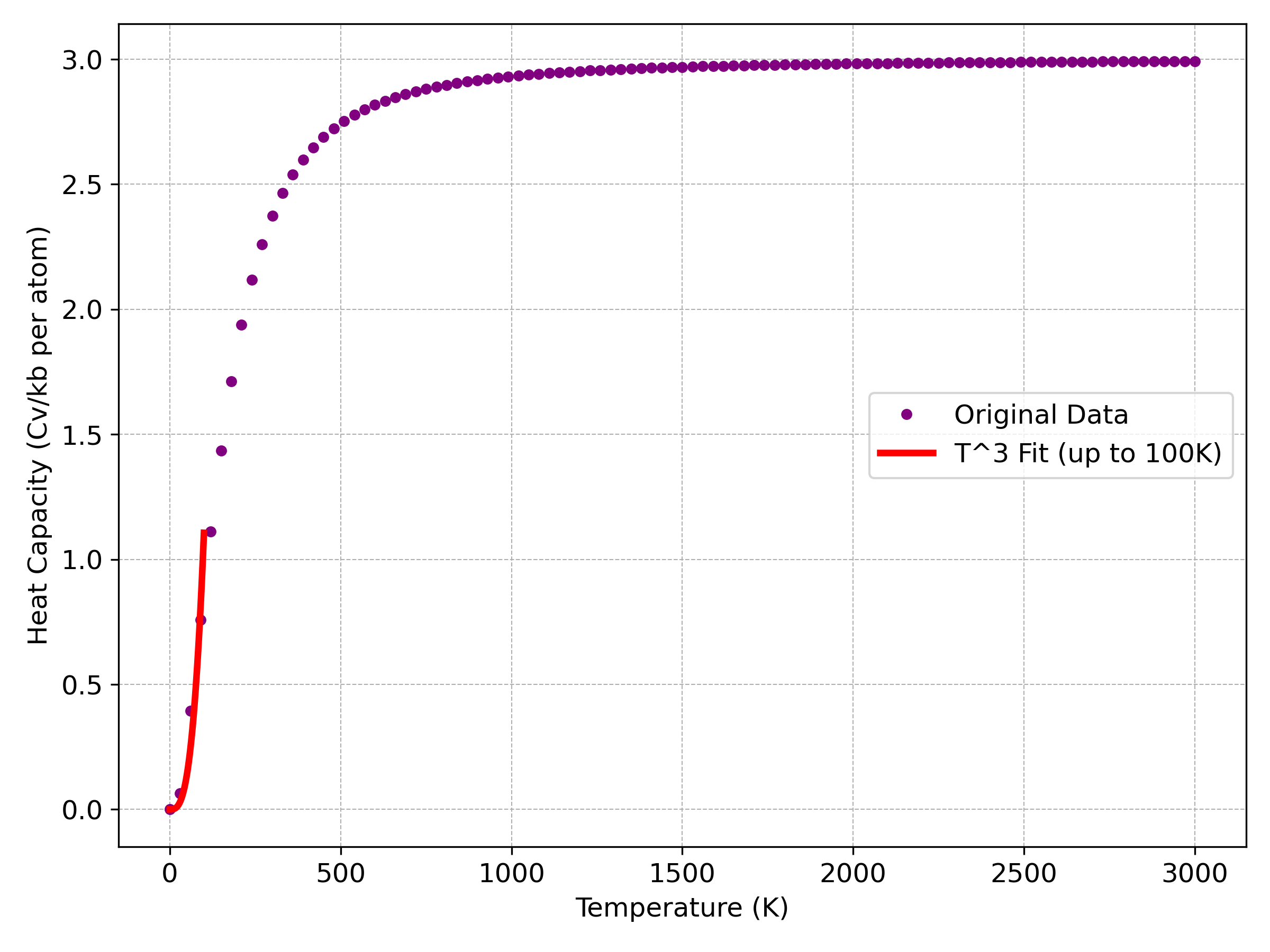
Siの比熱の温度依存性
図3.　比熱( $C_V$ )の温度依存性。紫色の点が計算データ、赤色の実線は100Kまでの $T^3$ を用いたフィッティングです。

図2から、温度の上昇に伴い、系の乱雑さを反映するエントロピー( $S$ )が増加し、ヘルムホルツの自由エネルギー( $F$ = $U - TS$ )が減少することがわかります。これは熱力学的に期待される振る舞いです。

図3の比熱( $C_V$ )は、極低温ではデバイモデルの示す通りに $T^3$ に比例して増加し、高温になるにつれて一定値に収束していく様子が明確に捉えられています。この高温での飽和値は、デュロン－プティの法則として知られる古典的な極限値（原子あたり $3k_B$ ）に漸近しており、計算が調和近似の枠組みで妥当であることを示しています。

比熱の計算値と実験値の比較#

本計算手法の妥当性をさらに検証するため、算出された比熱( $C_V$ )と実験値を比較しました(図4)。実験値は、信頼性の高い熱力学データ集 [4]から引用し、定圧比熱( $C_p$ )から熱力学関係式を用いて定積比熱( $C_V$ )に換算したもの、および文献 [5]のグラフから読み取った低温領域のデータを使用しています。

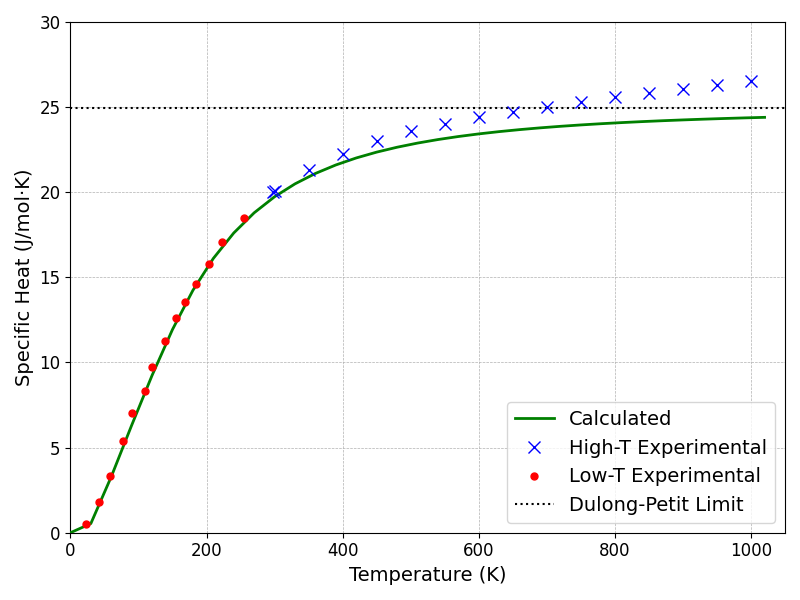
図4.　計算された比熱($C_V$)と実験値の比較。実線が本研究の計算値、マーカーが実験値を示す。

図4から明らかなように、本手法による計算結果は、低温から高温に至る広い温度範囲で実験値と非常に良好な一致を示しています。特に、低温領域では計算値と実験値がほぼ重なっています。一方、高温領域では、実験値がデュロン－プティの法則の示す理論極限から徐々にずれて大きくなる様子が観測されます。これは、本計算で用いた調和近似の範囲を超える物理現象、すなわち非調和格子振動と電子励起の影響によるものと考えられます。

【補足】フォノン状態密度へのLO-TO分裂の影響について#

フォノン状態密度は、第一ブリルアンゾーン全域にわたるフォノン分散関係を波数ベクトル $q$ で積分することにより得られます。極性結晶、すなわちイオン性結晶においては、長距離クーロン相互作用に起因する巨視的電場が生じます。この電場の影響により、ブリルアンゾーン中心( $\Gamma$ 点, $q \approx 0$ )近傍で、光学フォノンブランチが縦波(Longitudinal Optical, LO)モードと横波(Transverse Optical, TO)モードにエネルギー的に分裂します。この現象はLO-TO分裂として知られ、フォノン状態密度に以下のような影響を及ぼします。

フォノン状態密度への寄与の限定性: LO-TO分裂が顕著に現れるのは、 $q \approx 0$ という極めて限定された位相空間の領域です。したがって、ブリルアンゾーン全体を積分して得られるフォノン状態密度の概形に対して、LO-TO分裂が支配的な寄与をすることはありません。
フォノン状態密度形状の変調: しかしながら、LO-TO分裂はフォノン状態密度の微細構造に対して無視できない影響を及ぼします。分裂によって生じるLOモードとTOモードのエネルギー差は、フォノン状態密度におけるピークのシフトや分裂、あるいは新たなエネルギーギャップの形成といった形で現れます。特に、フォノン分散関係における平坦な領域（フォノン状態密度のファン・ホーベ特異点）がこの分裂の影響を受ける場合、フォノン状態密度の形状に明確な変化が観測されます。
熱的特性との関連: フォノン状態密度は、ヘルムホルツの自由エネルギーや定積熱容量といった熱力学的物性を算出するための基礎量です。したがって、LO-TO分裂に起因するフォノン状態密度の変化は、これらの物理量を精密に評価する上で考慮すべき重要な因子となります。

本解析で対象としたシリコン(Si)は、典型的な共有結合性結晶であり、有効電荷が極めて小さいため、LO-TO分裂効果は通常考慮されません。この効果は、MgOに代表されるようなイオン性結晶の熱的特性を精密に議論する際に重要となります [3]。

まとめ#

本解析では、第一原理計算ソフトウェアAdvance/PHASE を用い、有限変位法によるフォノン解析からシリコンの熱的特性を算出する手法を示しました。精密な構造最適化に基づきフォノン状態密度を計算することで、自由エネルギー、エントロピー、比熱といった重要な物性値の温度依存性を第一原理計算から高精度に予測できることが確認できました。本手法は、様々な材料の熱力学的性質を評価するための有力なツールとなります。

参考文献#

A. Togo, and I. Tanaka, "First principles phonon calculations in materials science", Scripta Materialia 108, 1 (2015).
W. Weber, "Adiabatic bond charge model for the phonons in diamond, Si, Ge, and α−Sn", Phys. Rev. B, 15(10), 4789 (1977).
A. R. Oganov, M. J. Gillan, and G. D. Price, "Ab initio lattice dynamics and structural stability of MgO", J. Chem. Phys. 118, 10174 (2003).
P. D. Desai, "Thermodynamic properties of iron and silicon", J. Phys. Chem. Ref. Data 15, 967 (1986).
S. K. Estreicher, M. Sanati, D. West, and F. Ruymgaart, "Thermodynamics of impurities in semiconductors", Phys. Rev. B 70, 125209 (2004).