コンテンツにスキップ

LO-TO分裂効果を考慮したフォノンバンドの計算#

PHASE logo

固体の熱伝導率や熱膨張、赤外吸収、ラマン散乱といった様々な熱的・光学的物性は、原子の集団的な振動である格子振動（フォノン）によって支配されます。したがって、材料のフォノンバンド構造（フォノン分散関係）を正確に理解することは、材料科学において極めて重要です。特に、酸化マグネシウム（MgO）のようなイオン結晶（極性材料）では、縦波光学モード（LO）と横波光学モード（TO）の間に「LO-TO分裂」と呼ばれる特有の現象が生じます。これは長距離の静電的相互作用に起因するため、その精密な予測には特別な計算手法が要求されます。本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、代表的なイオン性結晶であるMgOを例として、LO-TO分裂を正確に再現するフォノンバンド計算の手法と結果を詳述します。

Keywords: 第一原理計算, フォノン, 格子振動, LO-TO分裂, 非解析項補正, イオン性結晶

計算手法#

フォノンバンド計算は、原子間の力（力定数）を求めることで行います。本解析では、短距離力と長距離力を別々に計算し、それらを組み合わせるハイブリッドアプローチを採用しました。

短距離力定数の計算：有限変位法 (Finite Displacement Method, FDM)#

短距離の原子間力定数は、有限変位法を用いて計算します。これは、スーパーセルモデル（基本単位格子を周期的に並べた拡大モデル）内の原子を個別に微小変位させ、その際に他の原子に働く力を第一原理計算で求め、変位と力の関係から力定数を算出する手法です。

長距離力の補正：非解析項補正 (Non-Analytic Term Correction, NACT)#

LOモードが誘起する長距離の静電場効果は、結晶全体にわたる電場の影響を受けます。この効果を正確に記述するためには、通常の周期境界条件を用いたフォノン計算では捉えきれない、波数ベクトルqがゼロに近づく極限で現れる特異な振る舞いを考慮する必要があります。この特異性を「非解析項」と呼び、これを補正することで、長距離のクーロン相互作用を適切にフォノンバンド計算に取り込むことができます。非解析項補正には、以下の2つの物理量が必要です。

  • ボルン有効電荷 (Born Effective Charge, ): 原子変位によって生じる分極の大きさを表す量。
  • 高周波誘電率 (High-Frequency Dielectric Constant, ): 電子の応答のみを考慮した誘電率。

これらの物理量は、基本単位格子に対して計算を行います。Advance/PHASEでは、図1に示すようにGUIから「Born effective charge」を選択するだけで、ベリー位相法を用いた高精度な計算を行うためのワークフローが自動的に生成されます。また、誘電率の計算についても、電子状態の計算結果を基に誘電率の計算プロジェクトをGUIで作成することが可能です。これにより、ユーザーは複雑な入力設定を行うことなく、スムーズに計算を実行でき、作業効率が大幅に向上します。

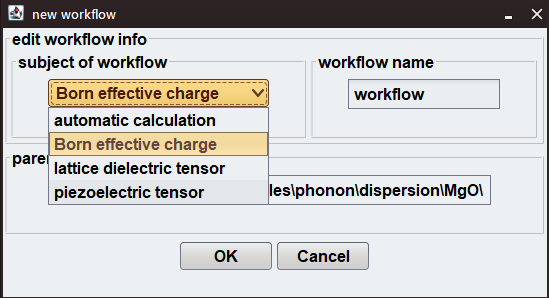
Born effective charge計算用のワークフロー作成GUI
図1. Born effective charge計算用のワークフロー作成GUI

最終的に、短距離と長距離の力を組み合わせて波数に依存する動的行列を構築し、対角化することでフォノン周波数を求めます。

\( D(\mathbf{q}) = D_{\text{FDM}}(\mathbf{q}) + D_{\text{NACT}}(\mathbf{q}, Z^*, \varepsilon_\infty) \)

計算モデル#

計算対象は岩塩（NaCl）型構造のMgOです。短距離力定数の計算には基本単位格子の2×2×2のスーパーセル（原子数16個）を使用しました。フォノンバンド構造は、面心立方（FCC）格子の第一ブリルアンゾーン（FBZ）内の高対称点を結ぶ経路（Γ-X-W-K-Γ-L-U-W-L-K-U-X）に沿って計算しました（図2）。結晶の対称性を反映したこれらの高対称点を通る経路に沿って計算することで、フォノンバンド構造の全体像を効率的に把握できます。

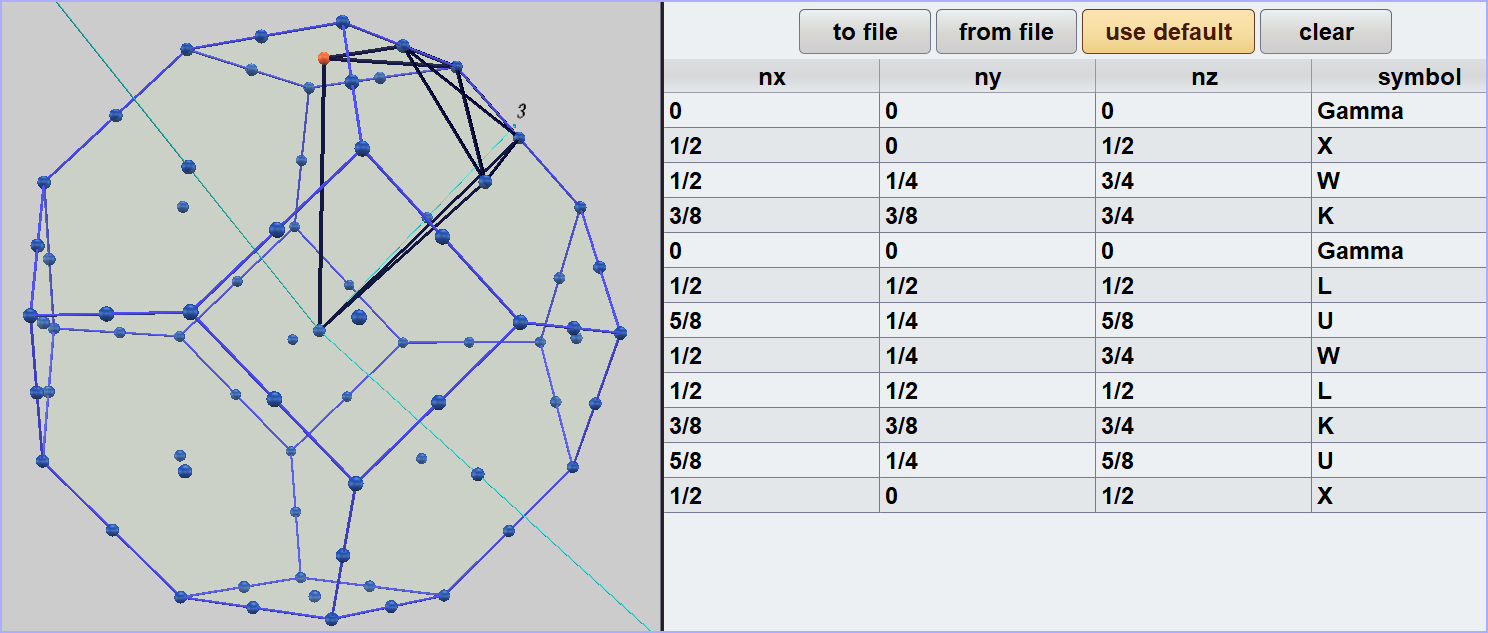
MgOの第一ブリルアンゾーンとk点経路
図2. MgOの第一ブリルアンゾーン（FBZ）とフォノンバンド計算のq点経路

計算結果と考察#

ボルン有効電荷と誘電率#

まず、非解析項補正に必要な物理量を計算しました。表1に高周波誘電率、表2にボルン有効電荷を示します。

表1. MgOの高周波誘電率テンソル

x y z
x 3.178 0.00 0.00
y 0.00 3.178 0.00
z 0.00 0.00 3.178

表2. MgOのボルン有効電荷テンソル

原子
Mg +1.951 +1.951 +1.951
O -1.951 -1.951 -1.951

MgOの立方晶対称性を反映し、誘電率は等方的な値を示しています。ボルン有効電荷は、形式的なイオン価数(Mg: +2, O: -2)よりも絶対値が小さい結果となりました。これは、Mg-O結合が完全なイオン結合ではなく、電子雲の応答に起因する共有結合性を帯びていることを示唆する、物理的に妥当な結果です。

フォノンバンド構造#

計算されたMgOのフォノンバンド構造を図3および図4に示します。図3は有限変位法を用いて計算した結果であり、図4はそれに非解析項補正を加え、イオン結晶に特有のLO-TO分裂を考慮した結果です。

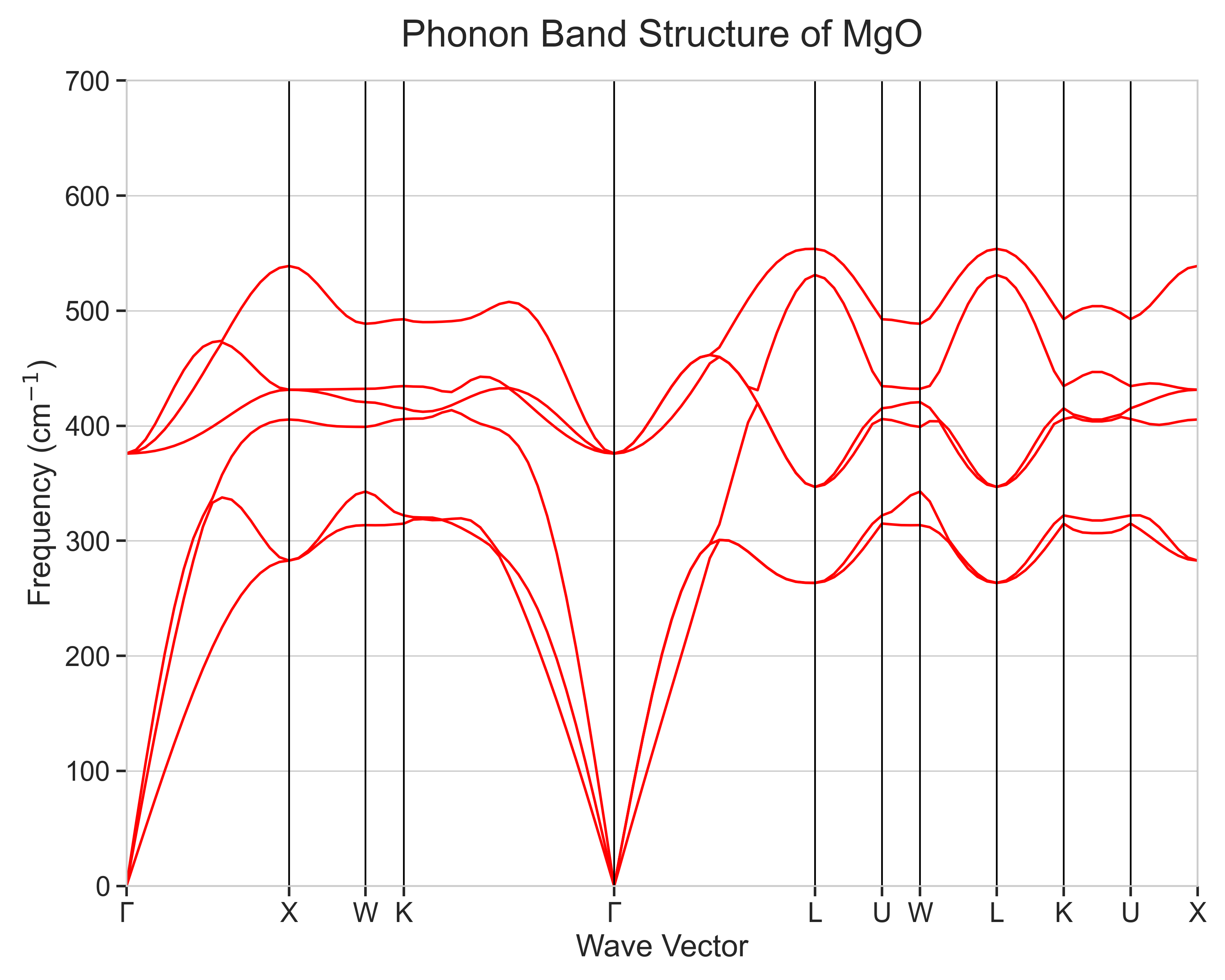
LO-TO分裂を考慮しないMgOのフォノンバンド構造
図3. LO-TO分裂を考慮しないMgOのフォノンバンド構造


LO-TO分裂を考慮したMgOのフォノンバンド構造
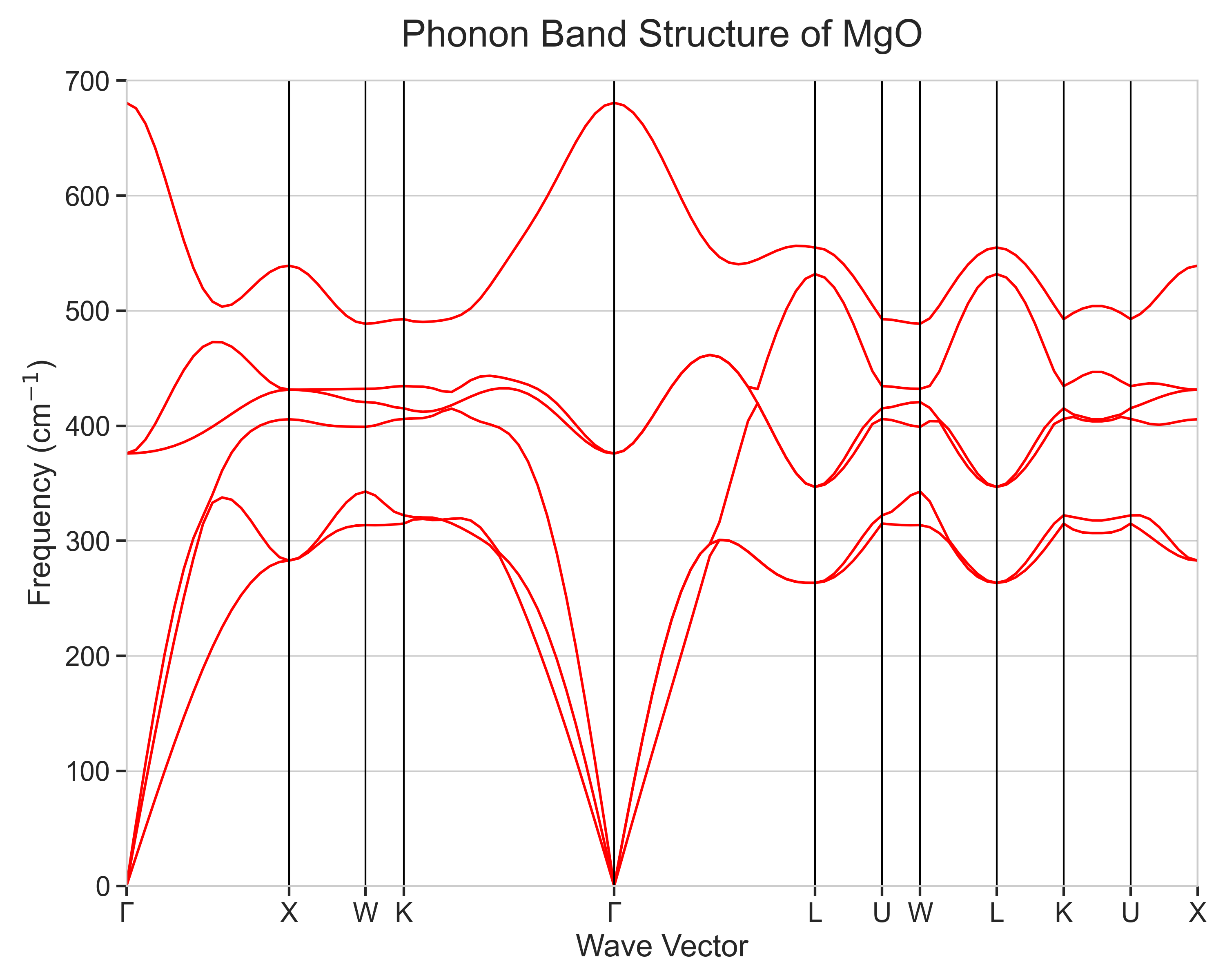
図4. LO-TO分裂を考慮したMgOのフォノンバンド構造

図4（LO-TO分裂を考慮した結果）から、以下の物理的に重要な特徴が確認できます。

  • フォノンブランチ：MgOの基本単位格子にはMg原子とO原子が1つずつ（合計2原子）含まれるため、フォノンブランチ（分散曲線）は音響モード3本、光学モード3本の合計6本となります。計算結果はこれを正しく再現しており、Γ点（波数ベクトルがゼロ）で周波数が0に収束する3本が音響モードに相当します。
  • LO-TO分裂： 本計算の最も重要な特徴として、Γ点における光学モードの縮退が解け、LO-TO分裂が明瞭に再現されています。TOモードが約376 cm-1 であるのに対し、LOモードの周波数は約681 cm-1 まで上昇しています。この約305 cm-1 のLO-TO分裂は、長距離の静電相互作用を記述する非解析項補正が正しく導入されたことを示しています。これらの値は実験 [2] で報告されていた、Γ点におけるTOモード・LOモードの周波数（それぞれ約394 cm-1、 約720 cm-1）およびそのLO-TO分裂値326 cm-1と良く一致しています。

全体的なバンドの形状や主要な対称点における周波数は、実験結果 [2] や他の計算事例 [3] とも良く一致しており、本計算の妥当性が支持されます。

まとめ#

本解析では、第一原理計算ソフトウェアAdvance/PHASEを用いて、イオン結晶MgOのフォノンバンド計算を行いました。短距離力を計算する有限変位法と、長距離の静電効果を扱う非解析項補正を組み合わせることで、実験的にも観測されるLO-TO分裂を、第一原理計算から再現できることを示しました。また、計算過程におけるGUIの活用は、複雑な設定を自動化し、解析効率を大幅に向上させます。

参考文献#

  1. P. Giannozzi, S. de Gironcoli, P. Pavone, and S. Baroni, "Ab initio calculation of phonon dispersions in semiconductors", Phys. Rev. B 43, 7231 (1991).
  2. M. J. L. Sangster, G. Peckham, and D. H. Saunderson, "Lattice dynamics of magnesium oxide", J. Phys. C: Solid State Phys. 3, 1026 (1970).
  3. A. R. Oganov, M. J. Gillan, and G. D. Price, "Ab initio lattice dynamics and structural stability of MgO", J. Chem. Phys. 118, 10174 (2003).

関連ページ#