TB-mBJポテンシャルを用いた半導体のバンドギャップ計算#

半導体の性能を決定づける最も重要な物理量の一つがバンドギャップです。密度汎関数理論（DFT）に基づく第一原理計算は材料開発に不可欠なツールですが、一般化勾配近似（GGA）などの汎関数を用いると、半導体のバンドギャップが実験値よりも著しく過小評価される問題が知られています。この問題を解決する手法の一つとして、メタGGA汎関数の一種であるTran-Blaha Modified Becke-Johnson（TB-mBJ）ポテンシャルがあります。本解析では、第一原理計算ソフトウェアAdvance/PHASEに搭載されたTB-mBJポテンシャルを用い、バンドギャップ計算の精度がどの程度向上するかを検証します。

Keywords: 第一原理計算, バンドギャップ, 半導体, DFT, TB-mBJ, GGA, PBE, Si, InP, GaN

TB-mBJポテンシャルの利用方法#

Advance/PHASEでTB-mBJポテンシャルを用いる際には、いくつかの注意点があります。まず、TB-mBJポテンシャルは電子状態計算に特化しており、原子に働く力を正確に計算できないため、構造最適化には利用できません。そのため、最初にPBEポテンシャル等で構造を最適化し、その後に得られた構造を用いてTB-mBJポテンシャルによる電子状態（バンドギャップ）の計算を行います。また、TB-mBJポテンシャルが利用できるのはノルム保存型擬ポテンシャルに限定されます。

解析結果と考察#

シリコン (Si) のバンドギャップ#

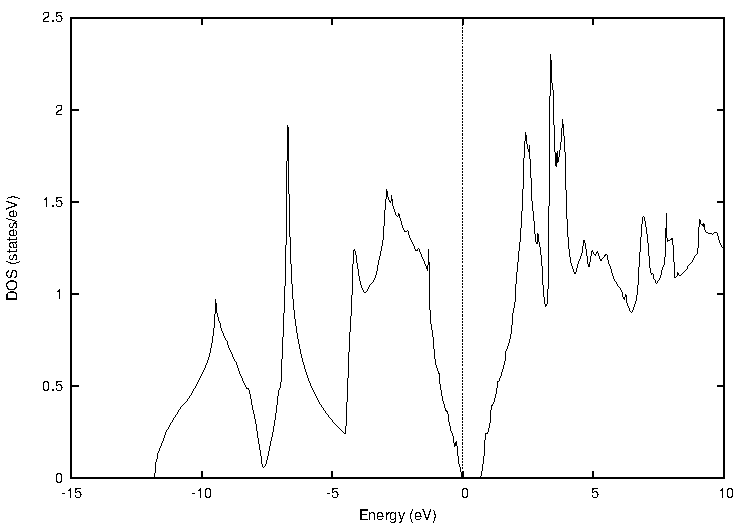
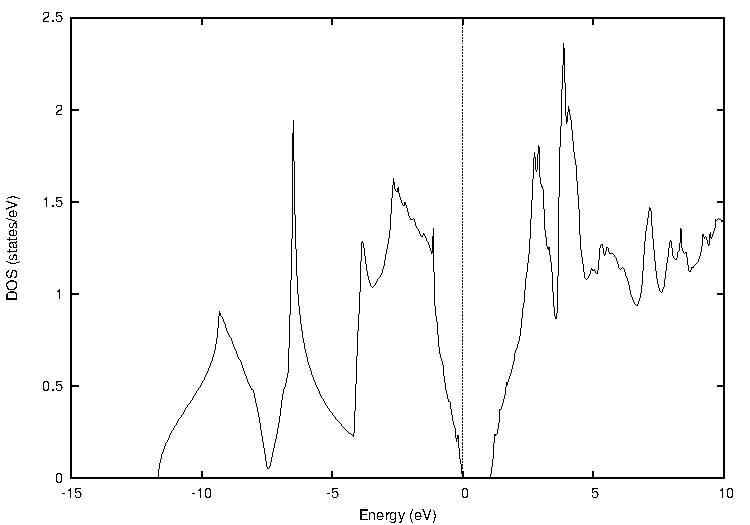
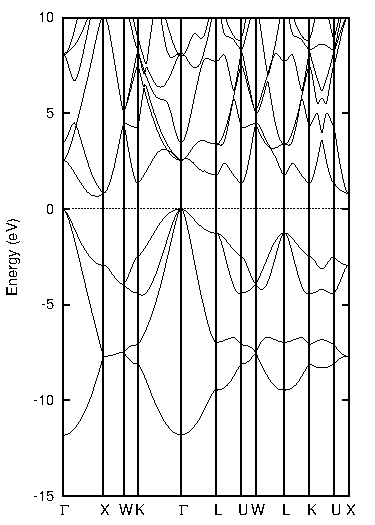
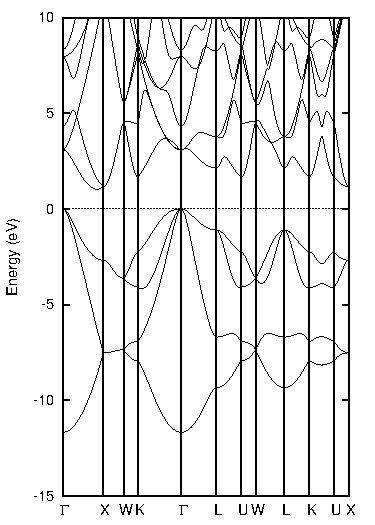
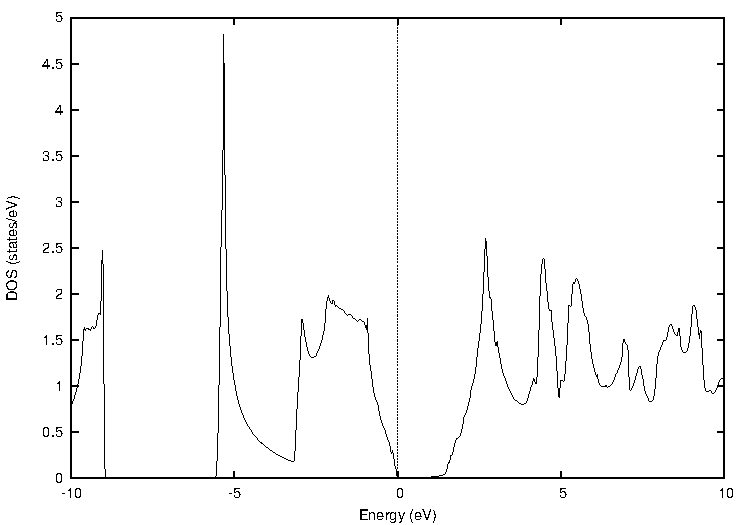
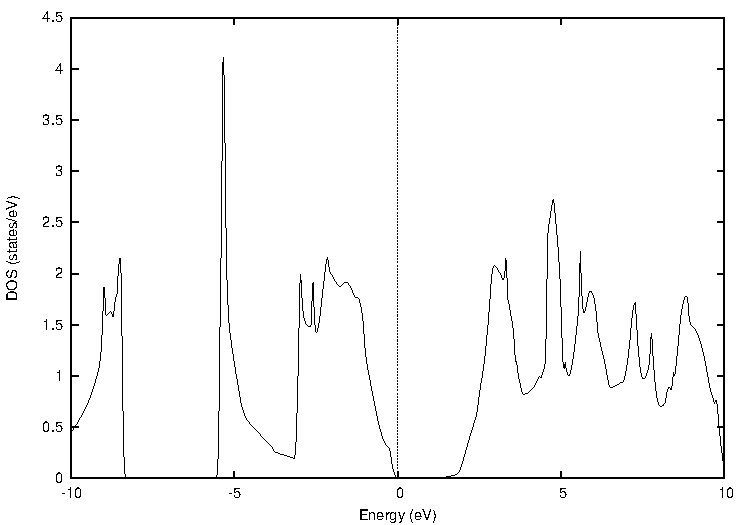
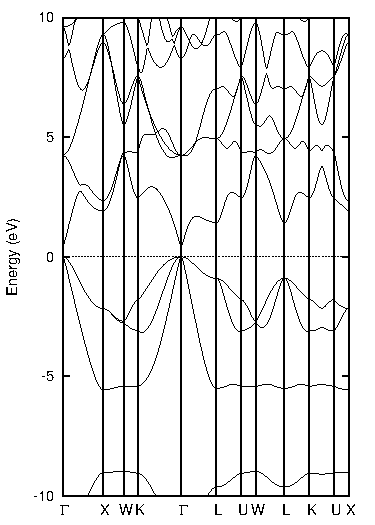
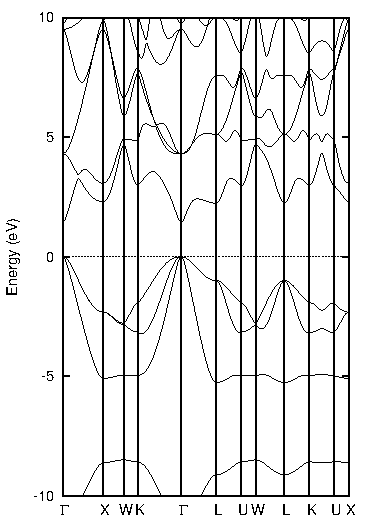
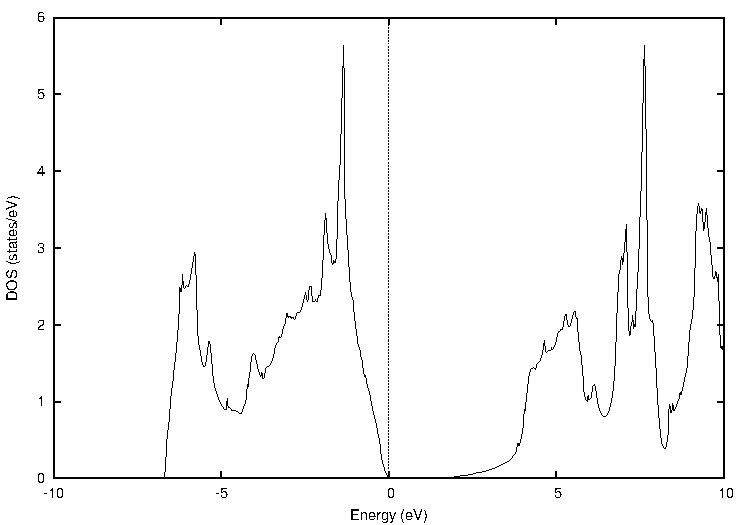
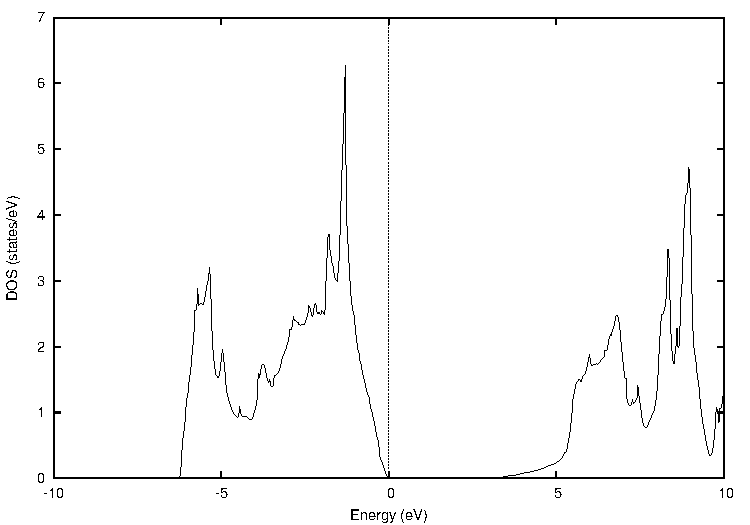
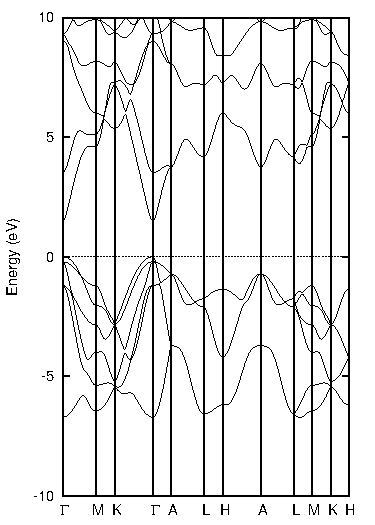
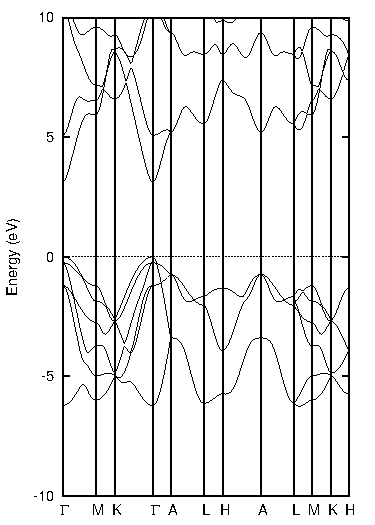
代表的な半導体であるシリコン（Si）について、標準的なGGA汎関数であるPBEとTB-mBJの計算結果を比較しました。図1に両手法による状態密度（DOS）とバンド構造を示します。バンド構造図では価電子帯上端と伝導帯下端の差から、状態密度図ではフェルミ準位（0 eV）を挟んだギャップの幅から、バンドギャップの大きさを見積もることができます。

図1. シリコン(Si)の計算結果

表1にバンドギャップの計算値と実験値をまとめます。PBEでは実験値(1.12 eV)を大きく過小評価していますが、TB-mBJを用いることで実験値との差が大幅に改善され、非常に近い値が得られました。

表1 シリコンのバンドギャップ比較 [eV]

PBE	TB-mBJ	実験値
0.66	1.03	1.12

その他の半導体への応用 (InP, GaN)#

インジウム・リン (InP)#

化合物半導体であるインジウム・リン（InP）について比較します（図2）。

図2. インジウム・リン(InP)の計算結果

表2に結果をまとめます。PBEではバンドギャップが0.44 eVと計算され、実験値（1.42 eV at 2 K）を大幅に過小評価していますが、TB-mBJでは1.44 eVと計算され、実験値と非常によく一致する結果となりました。

表2 インジウム・リンのバンドギャップ比較 [eV]

PBE	TB-mBJ	実験値
0.44	1.44	1.42

窒化ガリウム (GaN)#

同様に、窒化ガリウム（GaN）についても計算しました（図3）。

図3. 窒化ガリウム(GaN)の計算結果

表3に示すように、PBEではバンドギャップが1.49 eVでしたが、TB-mBJでは3.12 eVとなり、実験値（約3.39 eV）との乖離が大幅に改善されていることがわかります。

表3 窒化ガリウムのバンドギャップ比較 [eV]

PBE	TB-mBJ	実験値
1.49	3.12	~3.39

結果に関する考察#

GGA汎関数がバンドギャップを過小評価する主な原因は、電子自身のクーロン反発を打ち消してしまう自己相互作用エネルギーの扱いにあります。TB-mBJポテンシャルは、電子の運動エネルギー密度を取り入れることで、この自己相互作用を効果的に補正します。その結果、電子がより局在化し、価電子帯と伝導帯のエネルギー差、すなわちバンドギャップがより正確に計算されると考えられます。

バンドギャップを正確に計算する他の手法として、ハイブリッド汎関数やGW計算などがありますが、これらは一般的に計算コストが非常に高くなります。TB-mBJポテンシャルは、GGA計算とほぼ同等のコストで、これらの高精度な手法に近い結果を得られる場合があるため、材料のスクリーニングなど、多数の計算を要する研究において非常に費用対効果の高い手法と言えます。

バンドギャップを正確に予測できることは、LEDや太陽電池などの光デバイスの発光・吸収波長を見積もったり、半導体デバイスの電気的特性を正しくシミュレーションしたりする上で不可欠です。本解析で示されたTB-mBJの精度は、新しい機能性材料の設計・開発を加速させる上で重要な役割を果たします。

まとめ#

第一原理計算ソフトウェアAdvance/PHASEを用い、GGA汎関数(PBE)とメタGGA汎関数(TB-mBJ)による半導体のバンドギャップ計算を比較しました。代表的な半導体であるSi、InP、GaNにおいて、TB-mBJポテンシャルを用いることで、PBE計算で生じていた実験値との乖離が大幅に改善され、より精度の高いバンドギャップが得られることを確認しました。

参考文献#

F. Tran and P. Blaha, "Accurate Band Gaps of Semiconductors and Insulators with a Semilocal Exchange-Correlation Potential," Phys. Rev. Lett. 102, 226401 (2009).