単原子空孔を持つグラフェンのSTMシミュレーション#

PHASE logo

グラフェンは炭素原子が蜂の巣状に結合したシート状物質であり、その優れた電気的・機械的特性から次世代の電子材料として注目されています。グラフェンの物性は、格子欠陥、特に原子が一つ欠損した「単原子空孔」の存在によって劇的に変化します。走査型トンネル顕微鏡（STM）は、このような原子スケールの欠陥周りの局所的な電子状態を可視化できる強力な実験手法です。本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、単原子空孔を持つグラフェンのSTM像をシミュレーションし、実験結果との比較を通じてその物理的背景を考察します。

Keywords: 第一原理計算, グラフェン, 格子欠陥, 単原子空孔, STMシミュレーション

計算手法とモデル#

電子状態計算には、密度汎関数理論（DFT）を用いました。STM像のシミュレーションは、Tersoff-Hamann理論 [1] に基づいています。この理論では、STM像は原子の物理的な配置を直接見るのではなく、フェルミ準位 $E_F$ 近傍の局所状態密度（LDOS）を反映したものと解釈されます。バイアス電圧Vをかけた際のトンネル電流 $I$ は、探針の先端位置 $\mathbf{r}$ における試料の局所状態密度 $\rho(\mathbf{r}, E)$ を用いて、以下の式で近似されます。 $I(\mathbf{r}, V) \propto \int_{E_F}^{E_F+eV} \rho(\mathbf{r}, E) dE$ この式の右辺は、バイアス電圧のエネルギー範囲でLDOSを積分したものに比例します。これは第一原理計算において部分電荷密度（Partial Charge Density）として計算・可視化することでSTM像のシミュレーションが可能になります。

本解析ではこのアプローチに基づき、バイアス電圧+0.2 Vに対応するエネルギー範囲（ $E_F$ から $E_F + 0.2\text{eV}$ まで）の部分電荷密度を計算しました。これは探針に対して試料の電位が低い状態であり、試料の非占有状態（伝導帯側の電子状態）を観測していることに対応します。そして、その電荷密度をグラフェン表面から一定の距離 (4 Å)にある平面（コンター面）上で可視化することにより、STM像を生成しました。

計算モデルは以下の手順で構築しました。まず、グラフェンの2原子単位格子（Primitive Cell）に対してセル最適化を行い、格子定数として 2.45640562 Å を得ました。この際、2つの炭素原子の分数座標は、データベースなどで見られる0.33333のような近似値ではなく、十分な桁数を取って(2/3, 1/3, 0), (1/3, 2/3, 0) になるように正確に表現される必要があります。次に、この最適化された単位格子を用いて7x7のスーパーセル（合計98原子サイト）を作成し、中央の炭素原子を一つ取り除くことで単原子空孔を導入しました。その後の構造最適化では、孤立欠陥の状態を模擬するため、スーパーセルの格子定数は固定したまま、原子座標のみを緩和しました。図1は、このようにして得られた構造最適化後の計算モデルです。Jahn-Teller効果により、空孔周りの2つの炭素原子が再結合して五員環を形成し、もう一つの原子が面から僅かに垂直方向（面外方向）にずれることで、欠陥の安定構造の対称性が低くなっていることがわかります。計算に用いた主な条件は以下の通りです。

項目	設定値
交換相関汎関数	GGA (PBE)
擬ポテンシャル	ウルトラソフト
波動関数カットオフエネルギー	25 Rydberg
k点サンプリング	4x4x1
スピン分極	あり

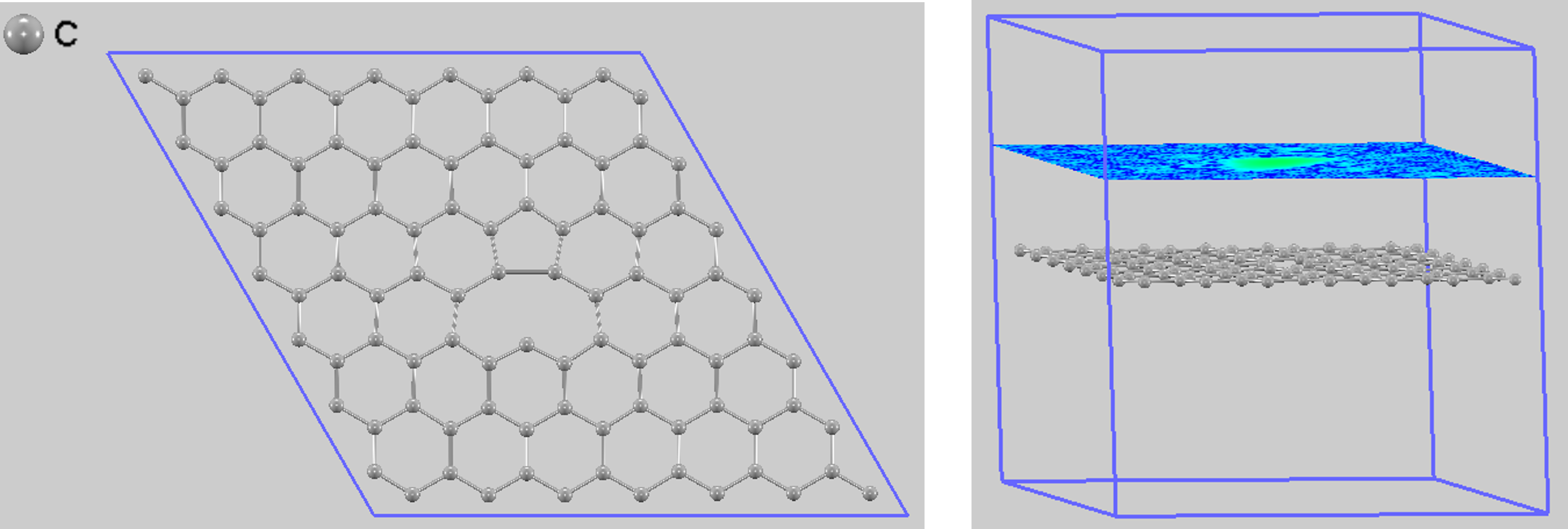
計算モデル

図1. 単原子空孔を含むグラフェンシートの計算モデル。左：Top view。右：Side view (上部の平面はSTM像を計算する高さ4Åのコンター面)。

結果と考察#

本シミュレーションにより、グラフェン単原子空孔周りの特徴的な原子構造、スピン状態、および局所電子状態（STM像）を明らかにしました。

スピン分極と欠陥誘起磁性#

単原子空孔の導入は、グラフェンの電子状態に劇的な変化をもたらします。図2は、空孔周りのスピン密度分布を示しています。上向きスピン（赤）と下向きスピン（青）が空間的に分極して分布しており、欠陥部分が磁気モーメントを持っていることがわかります。特に、Jahn-Teller効果によって面外方向に変位した炭素原子（図1参照）の位置には、原子軌道のような形状の強いスピン分極が局在しています。これは、結合相手を失った炭素原子の電子（σダングリングボンド）がスピン分極していることを示唆しています。同時に、周囲のπ電子系にもスピン分極が広がっており、σ電子とπ電子の両方がこの欠陥誘起磁性に寄与していることが示唆されます。この特徴は、文献[2] での報告とも一致しています。

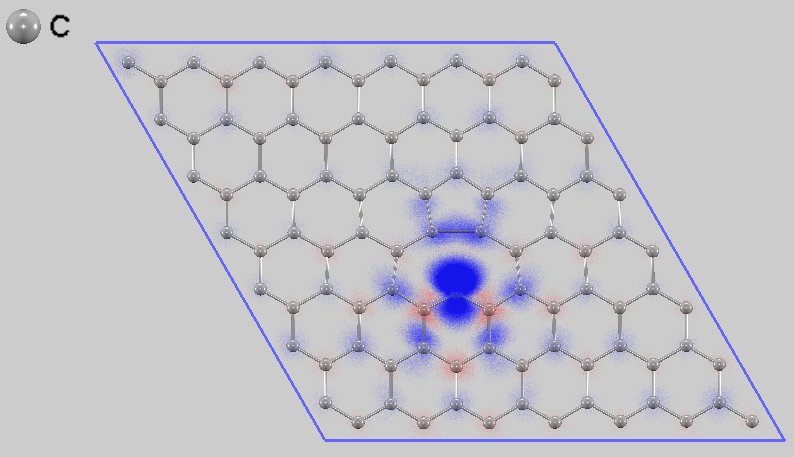
スピン密度分布

図2. スピン密度分布。赤色が正、青色が負のスピン密度を示す。空孔中心部に強いスピン分極が確認できる。

STM像のシミュレーションと実験との比較#

バイアス電圧+0.2VにおけるSTM像#

図3に、バイアス電圧+0.2VでシミュレートしたSTM像を示します。この像は、フェルミ準位から+0.2eVまでのエネルギー範囲にある非占有状態の局所状態密度(LDOS)を反映したものです。

2回対称性のパターン: 空孔の中心には輝度の高い領域が現れ、その周りには特徴的な2回対称性のパターンが形成しています。これは、図1に示したJahn-Teller歪みによる原子構造の対称性の低下（D₃hからC₂vあるいはそれ以下の低い対称性へ）が、電子状態の空間分布に直接反映された結果です。この結果、文献 [2]での報告と一致しています。
√3×√3-R30° 超周期構造: 空孔から離れた領域では、グラフェン格子とは周期の異なるパターンが広がっています。これは√3×√3-R30° 超周期構造として知られ、図4にその単位胞を赤色の六角形で示すように、欠陥によって電子が散乱されることで生じる量子干渉縞です [2-5]。

STM像 (+0.2 V)

図3. バイアス+0.2 VでのSTM像。欠陥周りの2回対称性と、遠方に広がる干渉パターンが確認できます。

√3×√3-R30° 超周期構造

図4. 図3のSTM像 (contour透明度：50%) に√3×√3-R30°の単位胞（赤色の六角形）を重ねたもの。電子の干渉による超周期構造が明瞭にわかります。

考察：静的・動的Jahn-Teller効果とSTM像の対称性

本シミュレーションで得られたSTM像は、原子構造とその電子状態を反映した2回対称性を示しました。一方で、実際のSTM実験 [3,4] では、+200 meVのバイアスの近くに、空孔周りに3回対称性の輝点が観測されることが報告されています。この違いはどのように解釈できるでしょうか。

その鍵は「動的Jahn-Teller効果」にあります。単原子空孔には、エネルギー的に等価な3つの歪んだ安定構造（五員環の向きが120°ずつ異なる）が存在します。本シミュレーションは絶対零度(0 K)での静的な状態を計算しており、そのうちの1つの構造（2回対称性）を捉えています。

しかし、室温などの有限温度下では、系は熱エネルギーによってこれら3つの等価な構造の間を高速で行き来します。STM測定のタイムスケール（通常はミリ秒単位）がこの遷移よりも十分に長い場合、観測されるSTM像は3つの構造の時間平均となり、結果として見かけ上の3回対称性が回復します [5]。

このように、シミュレーションと実験結果の比較検討から、欠陥の静的な構造だけでなく、その動的な振る舞いまで推察することが可能です。

まとめ#

本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、単原子空孔を持つグラフェンのSTMシミュレーションを実施しました。その結果、Jahn-Teller効果による原子の再構成や、それに伴う局所的なスピン分極（磁気モーメント）の誘起を理論的に確認しました。さらに、バイアス電圧+0.2VでのSTM像シミュレーションにより、欠陥中心の非対称な輝点パターンと、電子散乱に起因する√3×√3-R30°超周期構造という、実験で観測される複数の特徴をよく再現しました。シミュレーションで得られた2回対称性の像と実験で観測される3回対称性の像との比較からは、後者が動的Jahn-Teller効果による時間平均の結果であるという物理的描像を強く支持する知見も得られました。これらの結果は、第一原理計算に基づくSTMシミュレーションが、ナノ材料における格子欠陥周りの複雑な電子物性を解明し、実験結果に潜む物理現象を深く理解するための強力なツールであることを示しています。

参考文献#

J. Tersoff and D. R. Hamann, "Theory of the scanning tunneling microscope", Phys. Rev. B 31, 805 (1985).
O. V. Yazyev and L. Helm, "Defect-induced magnetism in graphene", Phys. Rev. B 75, 125408 (2007).
M. M. Ugeda, I. Brihuega, F. Guinea, and J. M. Gómez-Rodríguez, "Missing atom as a source of carbon magnetism", Phys. Rev. Lett. 104, 096804 (2010).
Y. Zhang et al., "Scanning tunneling microscopy of the π magnetism of a single carbon vacancy in graphene", Phys. Rev. Lett. 117, 166801 (2016).
H. Amara, S. Latil, V. Meunier, P. Lambin, and J. C. Charlier, "Scanning tunneling microscopy fingerprints of point defects in graphene: A theoretical prediction", Phys. Rev. B 76, 115423 (2007).