代表的な2次元単層材料のSTM像の第一原理解析#

グラフェン、単層六方晶窒化ホウ素(h-BN)、単層二硫化モリブデン(MoS2)に代表される2次元単層材料は、そのユニークな物理的・化学的特性から、次世代のエレクトロニクスや触媒材料として世界中で精力的に研究されています。これらの材料の物性を原子レベルで理解する上で、走査型トンネル顕微鏡(STM)は極めて強力な分析ツールです。STMは表面の原子構造だけでなく、電子状態に関する情報も与えてくれますが、その像の解釈は必ずしも直感的ではありません。本解析では、第一原理計算ソフトウェアAdvance/PHASE を用い、代表的な2次元材料のSTM像をシミュレーションし、その見え方が材料のどのような電子状態を反映しているのかを明らかにします。
Keywords: 第一原理計算 (DFT), 2次元単層材料, グラフェン, h-BN, MoS2, STM像シミュレーション, 部分電荷密度
計算モデルと計算条件#
本解析では、代表的な3種類の2次元単層材料、(a)グラフェン、(b)h-BN、(c)MoS2を対象としました。それぞれの原子構造を図1に示します。これらの図は、視覚的な分かりやすさのために3x3のスーパーセルで表示していますが、実際の計算はより基本的な単位であるプリミティブセル(primitive cell)を用いて効率的に行われました。
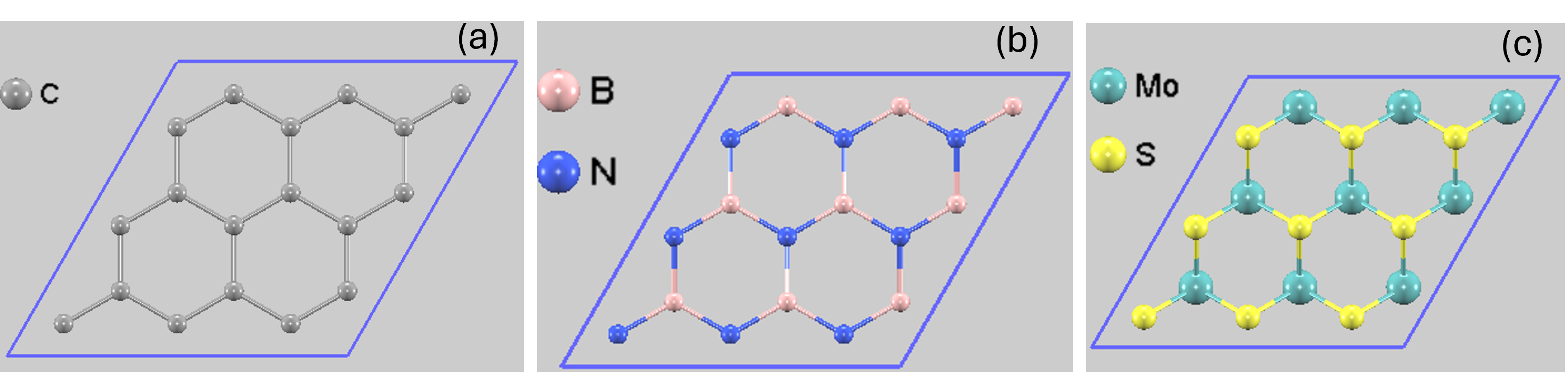
図1. 計算に用いた2次元単層材料の計算モデル: (a) グラフェン (b) 単層h-BN (c) 単層MoS2
STM像のシミュレーションは、Tersoff-Hamann理論 [1] に基づき行います。この理論では、トンネル電流は探針直下の電子状態密度に比例すると近似され、本解析ではフェルミ準位からバイアス電圧のエネルギー範囲に存在する電子の空間分布(部分電荷密度)を計算しました。今回は特に、サンプルから探針へ電子が流れる状態、すなわち試料の占有状態(occupied states)を反映する像に注目しました。具体的な計算条件は表1の通りです。
表1. 計算条件の概要
| 項目 | 設定 |
|---|---|
| 交換相関汎関数 | GGA (PBE) |
| 擬ポテンシャル | ウルトラソフト擬ポテンシャル |
| 波動関数のカットオフエネルギー | 25 Rydberg (約340 eV) |
| STM像のバイアス電圧 | -1.0 V (フェルミ準位から-1.0 eVまでの占有状態を積分) |
計算結果と考察#
グラフェン#
図2にグラフェンの計算結果を示します。上図は、バイアス電圧-1.0Vに対応する部分電荷密度の等値面(黄色い球状の領域)です。炭素原子の位置に電子が局在していることが分かります。これを反映し、下図のSTMシミュレーション像では、全ての炭素原子の位置に輝点(明るいスポット)が観察されます。これは、グラフェンを構成する炭素原子が全て化学的に等価であり、同じ電子状態を持つため、蜂の巣格子がそのままSTM像として現れることを示しています。
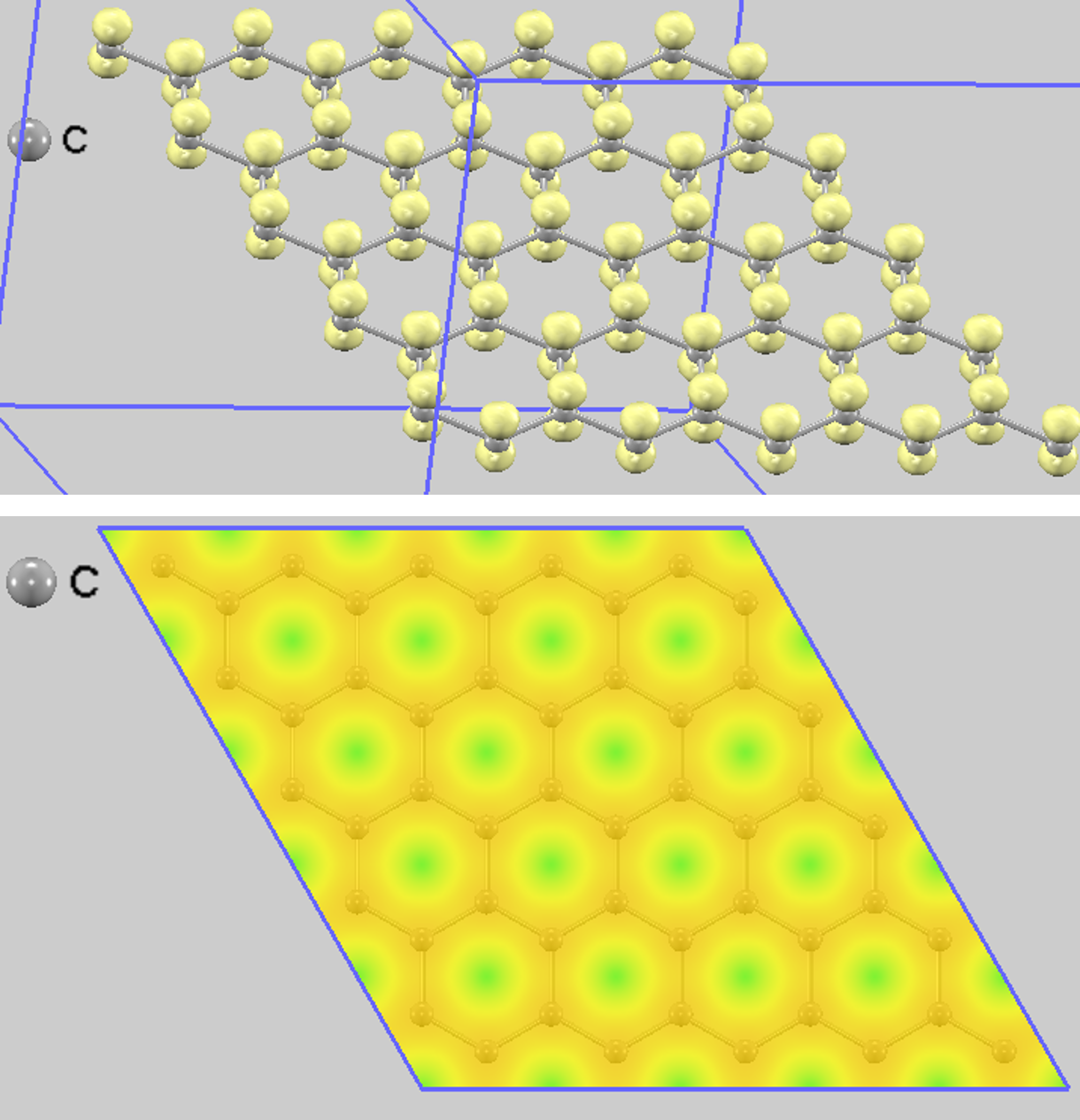
図2. グラフェンの計算結果。上:部分電荷密度の等値面、下:STMシミュレーション像。
単層h-BN#
次に、グラフェンと同じ蜂の巣構造を持つh-BNの結果を図3に示します。h-BNでは、ホウ素(B)と窒素(N)という2種類の原子が交互に配置されています。部分電荷密度(上図)を見ると、電子は主にN原子の周りに分布しており、B原子の周りにはほとんど存在しません。これは、N原子がB原子よりも電気陰性度が大きく、価電子を引きつける性質が強いためです。その結果、STMシミュレーション像(下図)では、N原子の位置のみが輝点として観察され、B原子の位置は暗く見えます。これにより、h-BNのSTM像はグラフェンとは対照的に、蜂の巣格子の一方の原子のみが光る三角形の格子模様として観察されます。
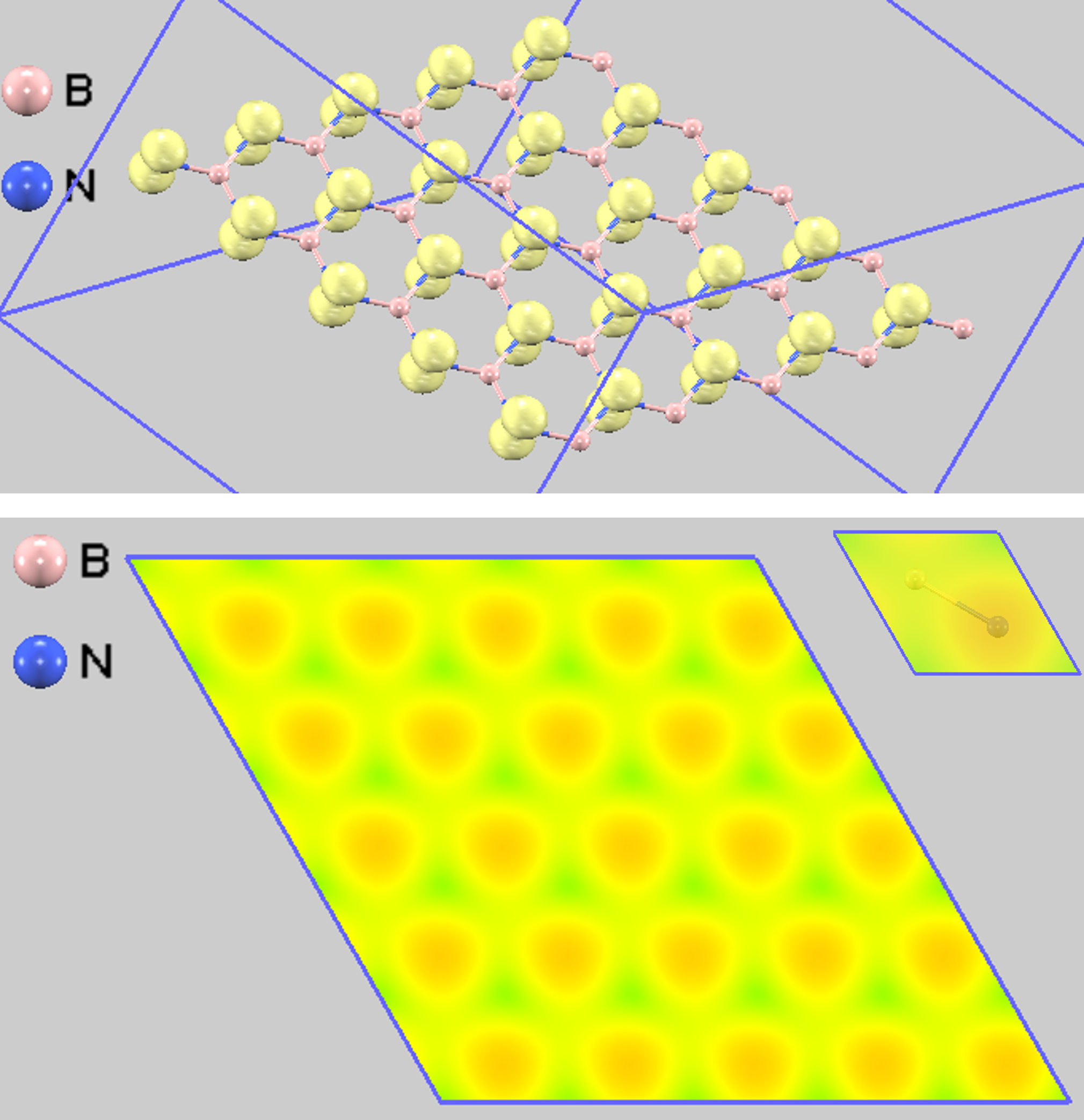
図3. 単層h-BNの計算結果。上:部分電荷密度の等値面、下:STMシミュレーション像。
単層MoS2#
最後に、遷移金属ダイカルコゲナイド(TMD)の一種であるMoS2の結果を図4に示します。MoS2は、Mo原子の層を上下からS原子の層が挟んだサンドイッチ構造をしています。上図の部分電荷密度を見ると、占有状態は主にMo原子のd軌道とS原子のp軌道から構成されていることが示唆されます。しかし、STMは表面から数Åの距離にある電子の染み出しを測定するため、最も表面に近い原子の情報が強く反映されます。その結果、STMシミュレーション像(下図)では、最上層に位置するS原子の配列に対応した輝点のみが観察されます。Mo原子はS原子の層の下に隠れているため、直接見ることはできません。
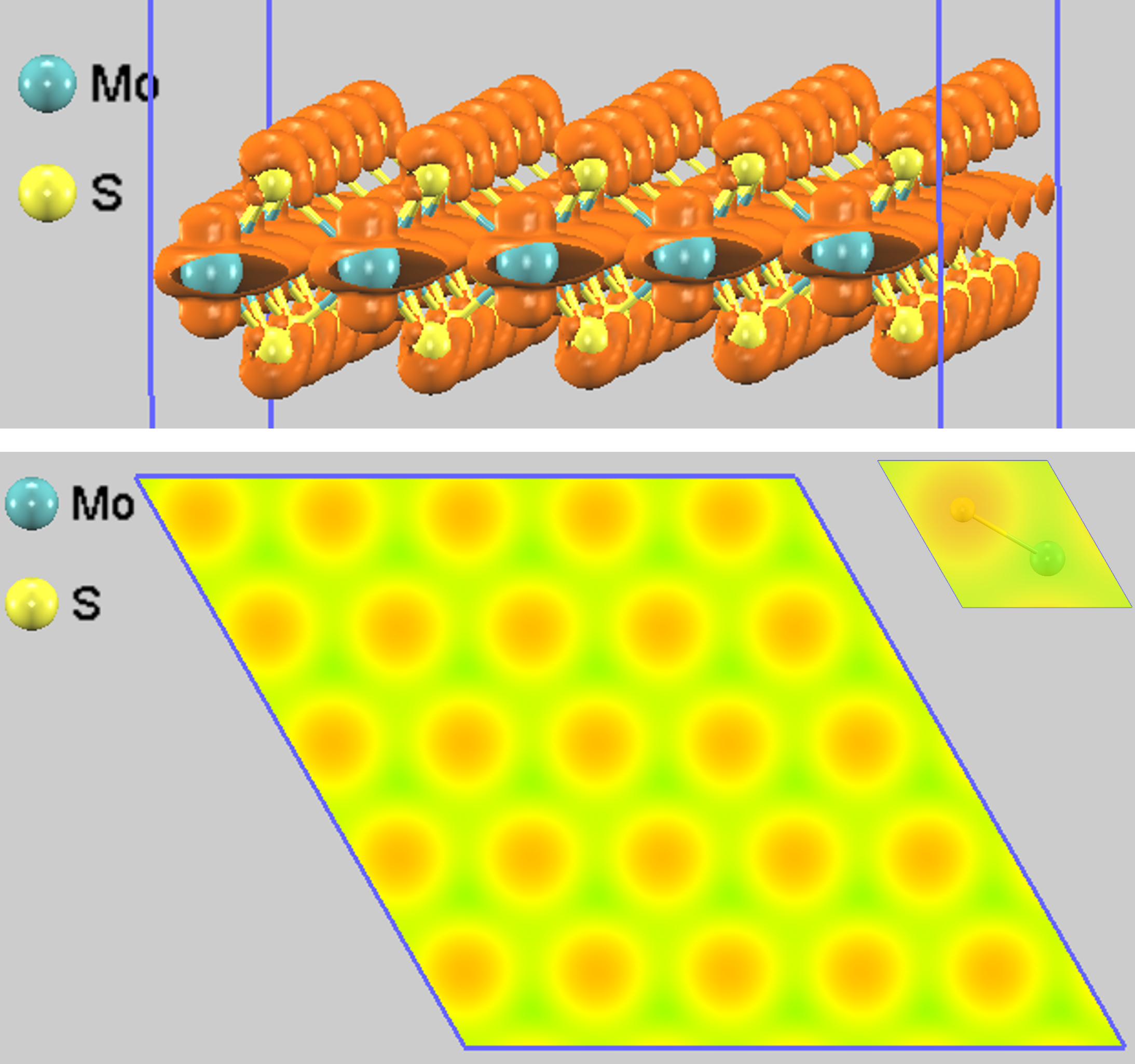
図4. 単層MoS2の計算結果。上:部分電荷密度の等値面、下:STMシミュレーション像。
考察:シミュレーションの妥当性と実在材料への展開#
今回のシミュレーションで得られたSTM像は、いずれも実験的に観測される特徴と非常によく一致しており、計算の妥当性を裏付けています。グラフェンの均一な蜂の巣格子、負バイアス下でのh-BNにおける窒素原子のみの可視化、そしてMoS2の最表面にある硫黄原子の配列といった特徴は、実験・理論の両面から確立された知見であり、本解析はこれらを正確に再現しました [2-4]。この結果は、STM像が原子の化学種(C, N, S)、電子状態(電気陰性度)、幾何学的配置(表面原子)をいかに敏感に反映するかを明確に示しています。
一方で、本解析は理想的な結晶を対象としましたが、実際のエピタキシャル成長させた試料には原子空孔(vacancy)や結晶粒界といった様々な「欠陥」が必ず存在します。これらの欠陥は局所的な電子状態を変化させ、STM像に特有のコントラストとして現れます。第一原理計算によるSTM像シミュレーションは、実験で観測された欠陥の正体を突き止め、その影響を解明する上で不可欠なツールとなります。
まとめ#
本解析では、第一原理計算ソフトウェアAdvance/PHASE を用いて、代表的な2次元単層材料であるグラフェン、h-BN、MoS2のSTM像シミュレーションを行いました。その結果、STM像に現れる輝点が、それぞれの材料の構成原子、化学結合、原子配列に由来する電子状態を敏感に反映していることを明らかにしました。具体的には、グラフェンでは全ての炭素原子が等価な輝点として、h-BNでは電子が豊富な窒素原子のみが輝点として、そしてMoS2では最表面に位置する硫黄原子のみが輝点として観察されました。これらの結果は、第一原理計算に基づくSTM像シミュレーションが、実験結果を解釈し、ナノスケールでの材料表面の電子状態を深く理解するための強力なツールであることを示しています。
本解析の詳細や、研究への適用可能性に関するご相談はこちら
お問い合わせ参考文献#
- J. Tersoff and D. R. Hamann, "Theory of the scanning tunneling microscope", Phys. Rev. B 31, 805 (1985).
- M. J. Allen, V. C. Tung, and R. B. Kaner, "Honeycomb carbon: a review of graphene", Chem. Rev. 110, 132 (2010).
- W. Auwärter, T. J. Kreutz, T. Greber, and J. Osterwalder, "XPD and STM investigation of hexagonal boron nitride on Ni (111)", Surf. Sci. 429, 229 (1999).
- P. Vancsó et al., "The intrinsic defect structure of exfoliated MoS2 single layers revealed by scanning tunneling microscopy", Sci. Rep. 6, 29726 (2016).
関連ページ#
- 第一原理計算ソフトウェア Advance/PHASE
- 解析分野:ナノ・バイオ
- 産業分野:材料・化学