希土類化合物の4f電子状態の解析#

PHASE logo

希土類元素を含む化合物は、そのf電子に由来する強い電⼦相関により、多彩な磁性や光学特性を示します。特に酸化ユウロピウム（EuO）は、強磁性半導体としての性質を持ち、スピントロニクス材料への応用が期待されています。これらの物性を正確に予測するためには、第一原理計算においてf電子の強い局在性を適切に取り扱うことが不可欠です。本解析では、第一原理計算ソフトウェアAdvance/PHASE を用い、EuOの電子状態と磁性をシミュレーションし、GGA+U法の有効性を検証します。

Keywords: 第一原理計算, GGA+U, 希土類, 4f電子, 酸化ユウロピウム, 磁気モーメント, 強磁性半導体

計算条件#

本解析では、低温で強磁性半導体として知られるEuO (岩塩型構造) [1] に対して、汎用的なGGA（PBE）汎関数を用いた計算と、GGAにオンサイト・クーロン相互作用Uを導入したGGA+U計算の2種類を⾏いました。U値を大きくするとバンドギャップは開く傾向がありますが、他の物性値との兼ね合いを考慮して適切な値を設定する必要があります。ここでUはEuの4f軌道に対して適⽤しました。その値は文献 [2,3] を参照して設定しました。主な計算条件は以下の通りです。

項目	設定
擬ポテンシャル	ウルトラソフト擬ポテンシャル
交換相関汎関数	GGA (PBE), GGA+U (Uf = 7.3 eV)
カットオフエネルギー	25 Rydberg
k点サンプリング (SCF)	8x8x8

計算結果と考察#

状態密度：GGAとGGA+Uの比較#

図1にGGA、図2にGGA+Uで計算されたEuOの状態密度（DOS）を⽰します。

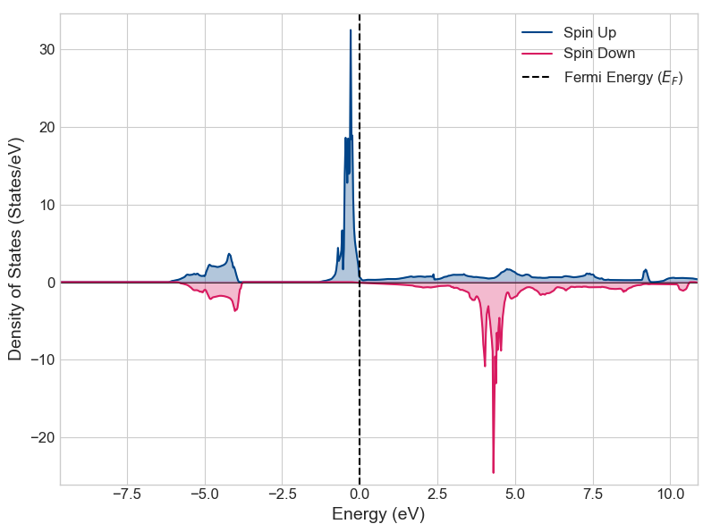
GGAによる状態密度

図1.　GGA計算による状態密度

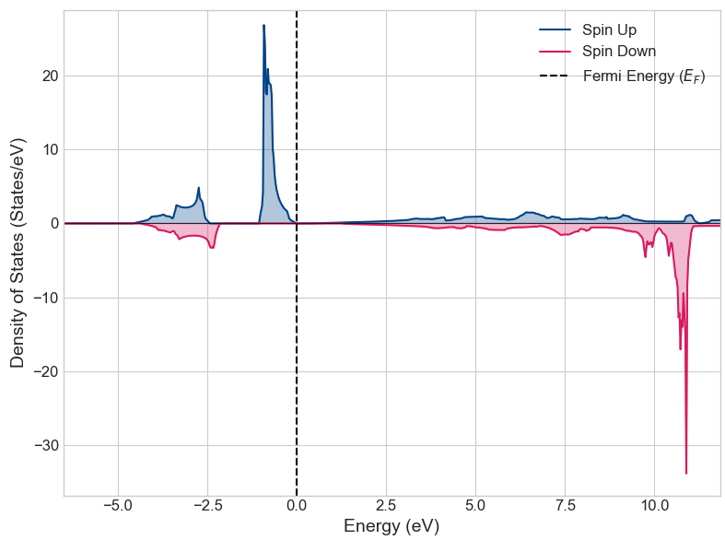
GGA+Uによる状態密度

図2.　GGA+U計算による状態密度

GGA計算（図1）: フェルミ準位（0 eV）で状態密度が有限の値を持ち、物質が金属的であることが示唆されます。これはEuOが半導体であるという実験結果と⼀致しません。
GGA+U計算（図2）: オンサイト・クーロン相互作⽤Uを導⼊することで、Euの4f電子の強い局在性が適切に記述されます。その結果、フェルミ準位にバンドギャップが開き、EuOが半導体であることが正しく再現されました。

この結果から、EuOのような強相関電子系材料の電子状態を正しく記述するには、GGA+U法が有効であることがわかります。

バンド構造と射影状態密度#

図3に、GGA+U法で計算したEuOのバンド構造を⽰します。価電⼦帯上端（VBM）がΓ点、伝導帯下端（CBM）がX点に位置しており、EuOが間接遷移型の半導体であることがわかります。計算されたバンドギャップは約0.41 eVでした。この「間接遷移」という結果は、実験やハイブリッド汎関数を用いた計算 [4] とも一致しており、本計算の妥当性を示唆しています。また、本計算で得られた強磁性状態におけるバンドギャップ値（0.41 eV）は、室温・常磁性状態での実験値（1.12 eV）[5] とは直接比較できないものの、ハイブリッド汎関数計算 [4] の予測範囲内にあり、定量的な妥当性も確認できます。

さらに、フェルミ準位近傍の電子状態の起源を探るため、Euの4f軌道に射影した状態密度（PDOS）を図4に示します。

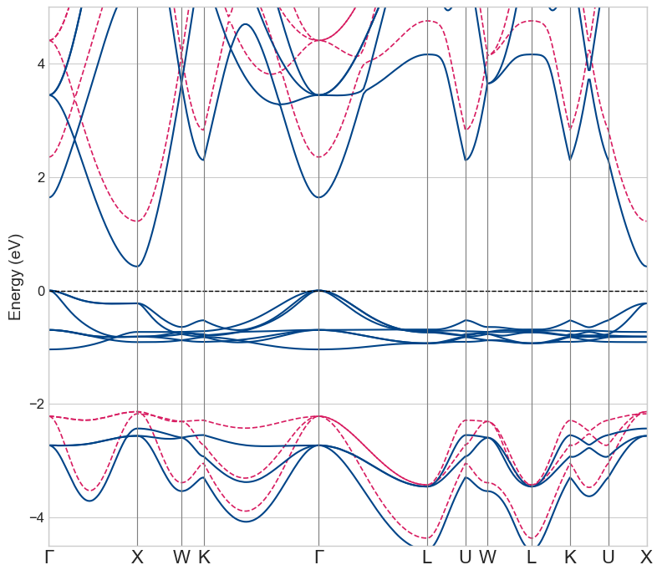
バンド構造

図3.　バンド構造 (GGA+U)

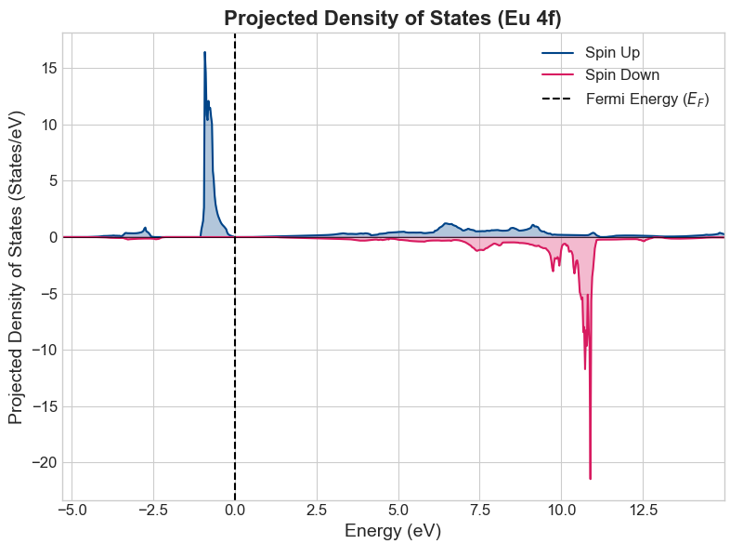
射影状態密度

図4.　射影状態密度 (Eu 4f)

図4から、価電子帯の最上部はアップスピンのEu 4f状態で構成されていることが明確にわかります。この4f電子の局在した性質が、EuOの物性を決定づけています。

磁気モーメントとスピン密度#

磁気モーメントは、アップスピンとダウンスピンの電子数の差から計算されます。計算された磁気モーメントは以下の通りで、GGAとGGA+Uで同じ値となりました。

表1.　計算された磁気モーメント（Eu原子あたり）

計算手法	磁気モーメント (μB)
GGA	6.955
GGA + U	7.000

この約7.0 μBという値は、Eu²⁺イオンの電⼦配置が[Xe] 4f⁷であることに起因します。フントの規則に従い、7つの4f電⼦がすべて同じ向き（アップスピン）に揃うことで、合計7 μBの磁気モーメントが⽣じます。Euの4f電子は非常に強く局在しているため、GGA計算でもこのスピン状態はよく再現されます。GGA+U法は電子の局在性をさらに強めますが、もともとほぼ完全にスピン偏極しているこの状態は変わらないため、磁気モーメントはほとんど変化しません。

図5は、スピン密度（アップスピン密度からダウンスピン密度を引いたもの）の分布を可視化したものです。等値面ではセル境界にあるEu原子が表示されていますが、断面図ではスピン密度分布の詳細を示すために境界にあるEu原子を表示していません。スピン密度の分布から、磁気モーメントがEu原子サイトに強く局在していることが視覚的に確認できます。

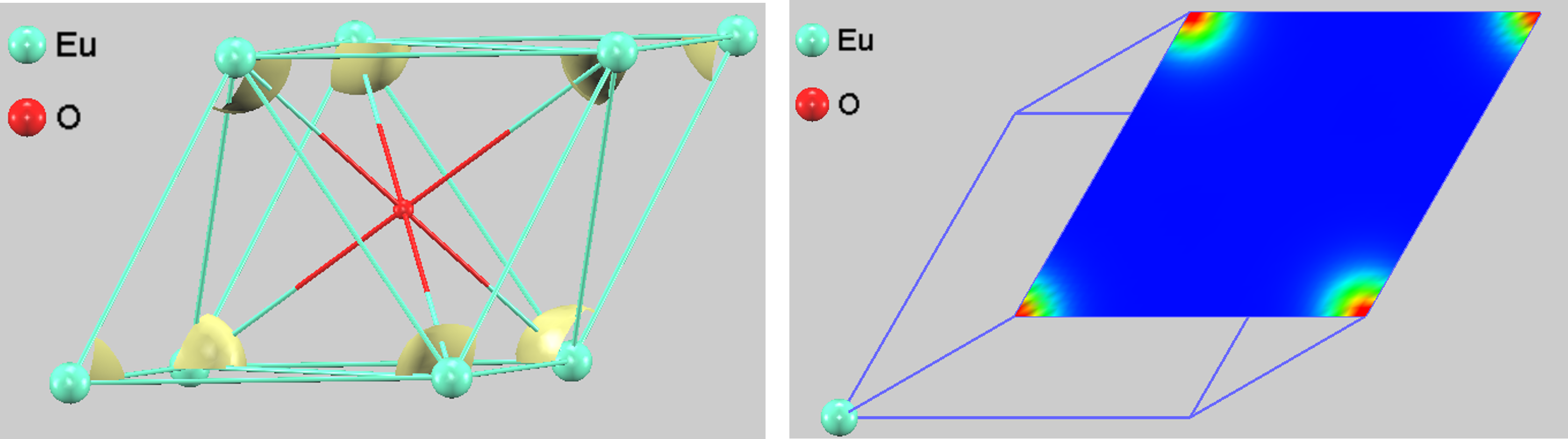
スピン密度（等値面と断面図）

図5.　基本単位格子におけるスピン密度分布。左：等値面 (境界原子の表示あり)、右：断面図（細部を見やすくするため境界原子の表示なし）。

部分電荷密度：結晶場分裂の可視化#

価電子帯を構成する4f電子の空間的な分布を調べるため、部分電荷密度を計算しました。図6では、2つの異なるエネルギー範囲で計算した部分電荷密度を比較しています。

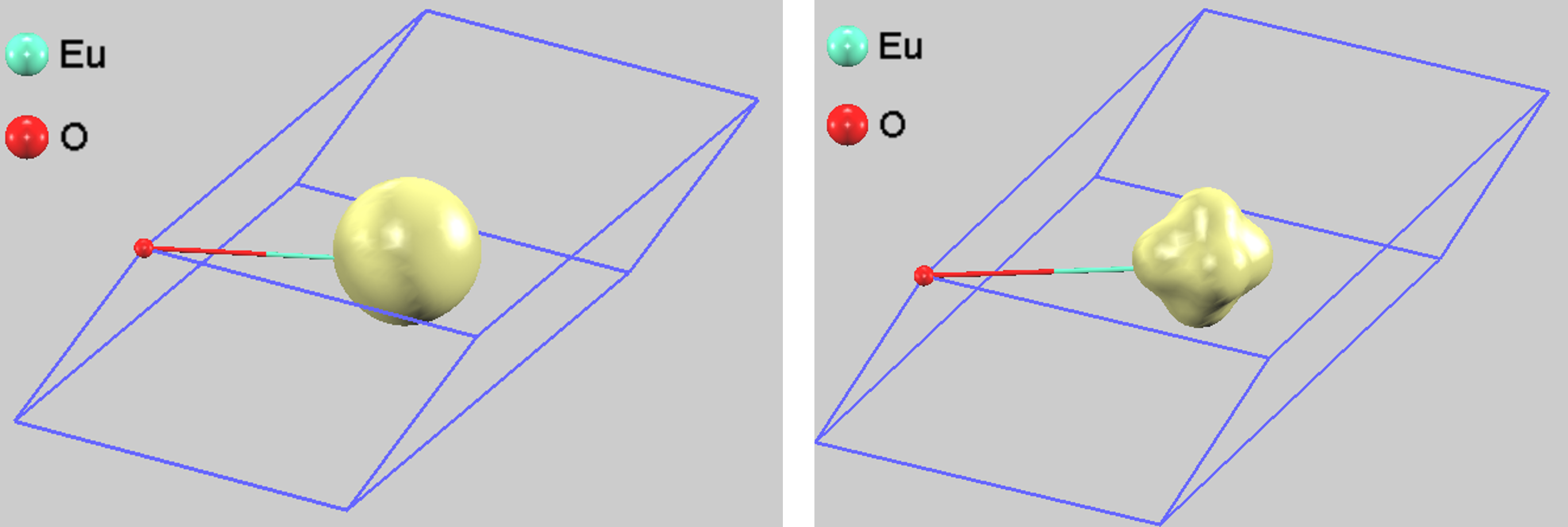
部分電荷密度の比較

図6.　Eu原子サイトを中心とした部分電荷密度（左：-1.0 eV ～ 0 eV、右：-0.5 eV ～ 0 eV）

左図（-1.0 eV ～ 0 eV）では、占有されたEu 4f状態のほぼ全域を含んでおり、電子密度は完全な球対称分布を示します。これは、電子が半分満たされた状態（半閉殻、4f⁷）の軌道を全て足し合わせると、合計の電子密度は必ず球対称になるというウンゼルトの定理 (Unsöld's theorem) [6] を反映した結果です。

一方、右図（-0.5 eV ～ 0 eV）は、価電子帯の最上部にある一部の4f状態のみを切り出したものです。結晶中では、周囲の酸素原子が作る結晶場の影響で7つの4f軌道のエネルギー準位が分裂します。このプロットでは分裂した準位の一部のみを足し合わせているため、個々の軌道の形状が反映された凹凸のある分布となり、完全な球対称性からのずれが生じています。

この2つの図の比較から、Eu²⁺の4f⁷電子状態の基本対称性は球形であること、そして結晶場がその縮退を解き、エネルギー準位によって電子分布を非等方にしている様子を明確に可視化できます。

まとめ#

本解析では、第一原理計算ソフトウェアAdvance/PHASEを用いて希土類化合物EuOの電子状態と磁性を解析しました。GGA計算では金属的な電子状態が予測されましたが、4f電子の強い相関を考慮するGGA+U法を適用することで、EuOが半導体であることが正しく再現されました。計算された磁気モーメントは7.0 μBであり、スピンが完全に整列したEu²⁺ (4f⁷) の電子状態と一致しました。状態密度や部分電荷密度の解析から、EuOの物性が強く局在した4f電子によって支配されていることが明確に示されました。GGA+U法は、このような強相関電子系の材料物性を解明するための有効な手法となります。

参考文献#

B. T. Matthias, R. M. Bozorth, and J. H. Van Vleck, "Ferromagnetic interaction in EuO", Phys. Rev. Lett. 7, 160 (1961).
P. Larson, W. R. Lambrecht, "Electronic structure and magnetism of europium chalcogenides in comparison withgadolinium nitride", J. Phys.: Condens. Matt. 18, 11333 (2006).
L. Petit, Z. Szotek, M. Lüders, and A. Svane, "Rare-earth pnictides and chalcogenides from first-principles", J. Phys.: Condens. Matt. 28, 223001 (2016).
M. Schlipf, M. Betzinger, M. Ležaić, C. Friedrich, and S. Blügel, "Structural, electronic, and magnetic properties of the europium chalcogenides: A hybrid-functional DFT study", Phys. Rev. B 88, 094433 (2013).
G. Güntherodt, P. Wachter, and D. M. Imboden, "Energy level scheme and the effect of magnetic order on the optical transitions in europium chalcogenides", Physik der kondensierten Materie 12, 292 (1971).
B. W. Pfennig, Principles of inorganic chemistry, John Wiley and Sons, 2015.