二成分密度汎関数法による陽電子シミュレーション：結晶中の原子空孔の解析#

PHASE logo

陽電子消滅法は、物質中の原子サイズの欠陥を鋭敏に検出できる強力な分析手法です。特に、原子空孔に陽電子が捕捉されると、その寿命が長くなる現象を利用して、欠陥のサイズや濃度を評価できます。空孔が複数個集まった「空孔クラスター」は、材料特性にさらに大きな影響を及ぼすため、その識別が重要となります。本解析では、第一原理計算ソフトウェアAdvance/PHASEに実装された二成分密度汎関数法を用い、半導体（Si）および金属（Al）における原子空孔と陽電子寿命の関係をシミュレーションし、欠陥サイズと寿命の相関を明らかにします。

Keywords: 第一原理計算, 陽電子寿命, 原子空孔, 空孔クラスター, 欠陥解析, 二成分密度汎関数法

計算手法と解析モデル#

陽電子寿命計算は、1個だけの陽電子の存在を想定して、電子と陽電子を量子力学的に取り扱う二成分密度汎関数法(Two-Component DFT) [1] に基づいて行います。まず通常の電子状態計算で系の電子密度 $\rho_e(r)$ を求め、その電子密度が作るポテンシャルの中で陽電子の状態（波動関数 $\psi_+(r)$ および密度 $\rho_p(r) = |\psi_+(r)|^2$ ）を計算します。

陽電子の消滅率 $1/\tau$ (寿命 $\tau$ の逆数)は、電子密度と陽電子密度の重なり積分によって、以下の式で評価されます。

$ \frac{1}{\tau} = \pi r_{e}^2 c \int{dr \rho_e \left( r \right) \rho_p \left( r \right) \Gamma \left( \rho_e \right)} $

ここで、 $r_e$ は電子の古典半径、 $c$ は光速です。 $\Gamma(\rho_e)$ は増大因子（enhancement factor）と呼ばれ、クーロン引力によって陽電子の周りに電子が引き寄せられ、局所的な電子密度が高まる効果を補正するものです。この式が示すように、陽電子が存在する場所の電子密度が低いほど、消滅率は小さく（寿命は長く）なります。

本解析では、Siの64原子、Alの108原子スーパーセルモデルをベースに、以下のモデルを対象としました。

完全結晶（Si, Al）
単原子空孔(V1)（Si, Al）
多原子空孔(V2, V3)（Si）

計算結果と考察#

Si完全結晶における電子・陽電子分布#

陽電子寿命を理解する上で、まず基準となる完全結晶中での電子と陽電子の分布を知ることが重要です。図1は、Si完全結晶における(a)価電子、(b)陽電子、(c)電子・陽電子対の分布を等値面で示しています。

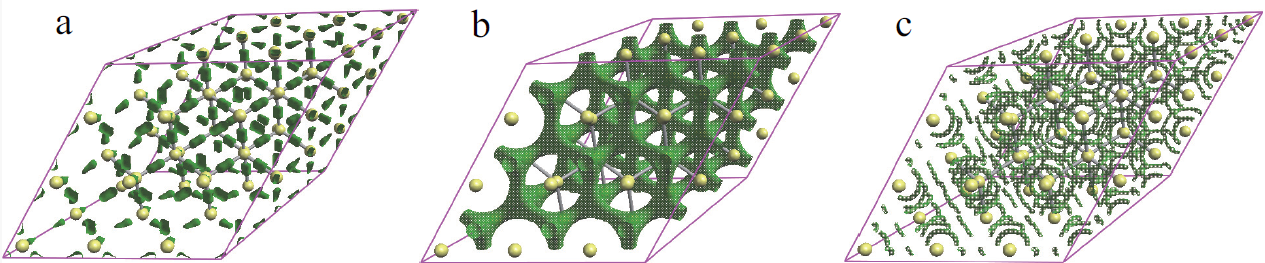
Si結晶における各種分布
図1.　Si完全結晶：(a) 価電子分布 (b) 陽電子分布 (c) 電子・陽電子対分布

価電子分布(a): Si原子間の共有結合を反映し、原子間に電子が密に存在しています。
陽電子分布(b): 正の電荷を持つ陽電子は、原子核との反発を避けるため、原子が存在しない格子間の空間（間隙サイト）に非局在的に分布します。
電子・陽電子対分布(c): これは電子と陽電子の分布の積で表され、陽電子が実際に消滅する確率が高い場所を示します。電子が豊富な結合領域と陽電子が存在する間隙領域の境界で、対分布が大きくなっていることがわかります。

Si原子空孔クラスターにおける陽電子のトラップ#

結晶中に原子空孔が存在すると、陽電子の状態は劇的に変化します。図2は、Si結晶中の空孔の数（1個、2個、3個）が増えるにつれて、陽電子の分布がどう変わるかを示したものです。

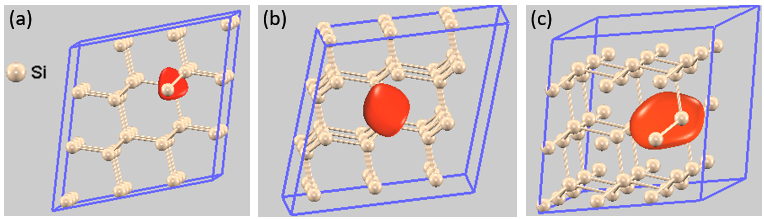
原子空孔1個(V1)の場合の陽電子分布
図2.　Si原子空孔クラスターにおける陽電子分布を示す等値面: (a) 原子空孔１個、(b) 原子空孔2個、(c) 原子空孔3個。等値面の色は、陽電子密度の最大値に対する相対的な割合を示します。

完全結晶では格子間に広がっていた陽電子が、単原子空孔(V1)があると、その欠陥サイトに強く束縛（トラップ）されます。これは、空孔が電子密度の低い「ポテンシャルの井戸」として機能するためです。さらに、空孔が2個(V2)、3個(V3)と集合するにつれて、陽電子がトラップされる空間はより大きく広くなります。この「トラップされる空間の拡大」が、陽電子寿命の系統的な変化に直結します。

金属(Al)における陽電子のトラップと寿命#

この陽電子のトラップ現象は、半導体だけでなく金属においても同様に重要です。図3は、単原子空孔（V1）を持つAlスーパーセルでの陽電子分布を示しています。

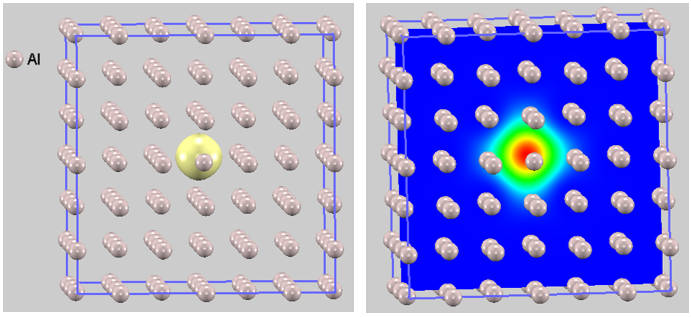
原子空孔を持つAlにおける陽電子分布
図3.　単原子空孔を持つAlスーパーセルにおける陽電子分布：(左) 等値面 (右) 断面図

Alの完全結晶中では陽電子が格子間に広く分布しますが、原子空孔が存在すると、Siの場合と同様に陽電子は欠陥サイトに強く局在化します。この局在化は陽電子が周囲の電子との遭遇確率が大幅に低下するため、陽電子寿命に劇的な影響を与えます。

陽電子寿命の定量評価：計算と実験の比較#

表1は各種欠陥における陽電子寿命を示しています。Si、Alのいずれにおいても、計算された陽電子寿命は実験値 [2, 3] と非常によく一致しています。

表1. 各種欠陥における陽電子寿命の計算値と実験値（単位: ps）

材料	状態	寿命 (計算)	寿命 (実験)
Si	完全結晶 (Bulk)	223	220
	V1 (空孔1個)	266	266±10
	V2 (空孔2個)	299	295~325
	V3 (空孔3個)	324	320±3
Al	完全結晶 (Bulk)	167	165
	V1 (空孔1個)	242	244

特にSiでは、空孔の数が増える（V1→V2→V3）につれて寿命が系統的に長くなる傾向が明確に捉えられています。空孔2個の場合、計算値 (299 ps)が実験値の範囲 (295~325 ps)に入っており、ほかの理論値（306 ps [4], 309 ps [5]）とも非常によく一致しています。Alの単原子空孔においても、計算値は実験値と極めて良好な一致を示しています。

構造緩和の効果に関する考察#

本解析事例では、原子の構造緩和（最適化）を行わずに計算した陽電子寿命が、実験値と非常に良い一致を示しました。一般に、欠陥が存在すると周囲の原子は構造緩和を起こすため、この結果は一見すると不思議に思えるかもしれません。しかし、これには明確な物理的背景が存在します。

欠陥周りの構造緩和を考える際には、主に2つの相反する効果を考慮する必要があります。

陽電子不在時の構造緩和： 原子空孔が形成されると、周囲の原子は不安定な結合（ダングリングボンド）を再構成しようとして内側へ移動します。これにより空孔の体積は縮小し、この状態で計算される陽電子寿命は短くなります。
陽電子による構造緩和： 空孔に捕捉された陽電子は、その正電荷によって周囲の原子核（こちらも正電荷）と静電的に反発します。この反発力は原子を外側へ押し出し、空孔の体積を拡大させます。この効果は陽電子寿命を長くします。

このように、「内向き緩和」と「外向き緩和」は互いに打ち消し合う方向に働きます。特にSiの中性空孔のような系では、これらの効果がほぼ相殺されることが知られています [5]。そのため、「構造緩和なし」という一見単純な計算が、結果的に物理的に妥当な寿命を与えるのです。

より厳密なアプローチとしては、陽電子の存在とそれによる力を考慮しながら原子の構造緩和を自己無撞着に行う計算手法があります。この手法は計算コストが高いものの、最も信頼性の高い結果をもたらすと期待されます [5, 6]。

まとめ#

本解析では、Advance/PHASEを用いて半導体Siと金属Alにおける原子空孔の陽電子シミュレーションを行いました。完全結晶中では格子間に分布する陽電子が、原子空孔の存在によって欠陥サイトに強くトラップされる様子が可視化されました。Si結晶において、空孔クラスターが大きくなるほど陽電子寿命が系統的に長くなるという、欠陥サイズと寿命の明確な相関を示しました。半導体Si、金属Alのいずれにおいても、計算された陽電子寿命は実験値と高い精度で一致しました。第一原理計算に基づく陽電子シミュレーションは、材料内部のナノスケールの欠陥構造を特定し、そのサイズや種類を定量的に評価するための有力な予測ツールとなります。

参考文献#

E. Boroński and R. M. Nieminen, "Electron-positron density-functional theory", Phys. Rev. B 34, 3820 (1986).
河裾厚男、長谷川雅幸、 "バルク半導体中の欠陥"、まてりあ 35, 130 (1996).
J. C. Robles, E. Ogando, and F. Plazaola, "Positron lifetime calculation for the elements of the periodic table", J. Phys.: Conden. Matt. 19, 176222 (2007).
M. J. Puska and C. Corbel, "Positron states in Si and GaAs", Phys. Rev. B 38, 9874 (1988).
M. Saito and A. Oshiyama, "Lifetimes of positrons trapped at Si vacancies", Phys. Rev. B 53, 7810 (1996).
M. J. Puska, A. P. Seitsonen, and R. M. Nieminen, "Electron-positron Car-Parrinello methods: self-consistent treatment of charge densities and ionic relaxations", Phys. Rev. B 52, 10947 (1995).