ペロブスカイト酸化物 CaTiO3 の構造相転移とソフトモード解析#

チタン酸カルシウム(CaTiO3)は、ペロブスカイト構造を持つ代表的な酸化物であり、誘電体材料や地球深部科学の分野で広く研究されています。この物質は高温(> 1580 K)では理想的な立方晶構造(Cubic)をとりますが、室温では構造歪みを伴う斜方晶(Orthorhombic)として安定化することが知られています。この構造相転移の起源を理解することは、材料の物性制御において極めて重要です。本解析では、第一原理計算ソフトウェアAdvance/PHASE を用い、高温相である立方晶に対して状態方程式(EOS)およびフォノン解析を行うことでその不安定性(ソフトモード)を特定し、さらにそのモードに沿った構造変形シミュレーションを行うことで、室温の安定構造である斜方晶への相転移過程を実験値と一致する高精度で再現しました。
Keywords: 第一原理計算, DFTシミュレーション, 構造相転移, フォノン解析, ソフトモード, ペロブスカイト, 格子歪み, 状態方程式
計算モデルと計算条件#
DFT計算は以下の手順で行いました。
(1) 理想的な立方晶 Pm-3m 構造に対し、体積を変化させながらエネルギーを計算し、状態方程式(EOS)を作成して平衡格子定数を決定しました。
(2) 得られた平衡構造を用いて 2x2x2 スーパーセル(40原子)を作成し、有限変位法によるフォノン計算を行いました。
(3) 検出された不安定モードに沿って原子を変位させたモデルに対し、セル形状を含む構造最適化を行い、最終的な安定構造を得ました。
DFTシミュレーションの主な計算条件は表1に示します。なお、セル形状の最適化(応力計算)における精度を確保するため、カットオフエネルギーは高めの設定(標準の1.5倍)としています。
表1. 計算条件の概要
| 項目 | 設定 |
|---|---|
| 擬ポテンシャル | ウルトラソフト擬ポテンシャル |
| 交換相関汎関数 | GGA (PBE) |
| カットオフエネルギー | 35 Rydberg |
| k点サンプリング | 各構造に対し十分に収束する点を設定 |
計算結果と考察#
1. 立方晶の状態方程式 (EOS)#
まず、高温相である理想的な立方晶構造について、体積に対する全エネルギー変化(EOS)を計算しました(図1)。
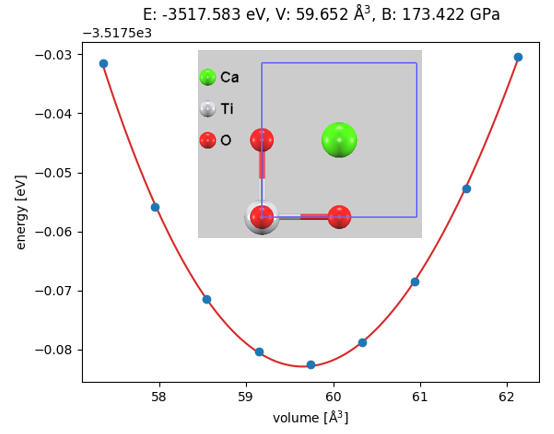
図1. 立方晶 CaTiO3 の状態方程式 (EOS)。計算値をBirch-Murnaghan方程式でフィッティングしています。
エネルギー曲線は綺麗な放物線を描いており、計算された平衡格子定数は a = 3.907 Å、体積弾性率 B = 173.4 GPa となりました。これは既存の実験値や理論値とよく一致しており、体積の変化(圧縮・膨張)に対してはこの構造が安定であることを示しています [1]。しかし、この状態方程式の計算では結晶の対称性を保っているため、局所的な構造歪みに起因する不安定性は現れません。そこで、構造の動的な安定性を調べるためにフォノン計算を行いました。
2. フォノンバンド分散とソフトモード#
平衡体積における立方晶のフォノンバンド分散を図2に示します。グラフの縦軸は振動数であり、0 cm-1 より下の負の値(虚の振動数)は、構造が不安定であることを意味します。
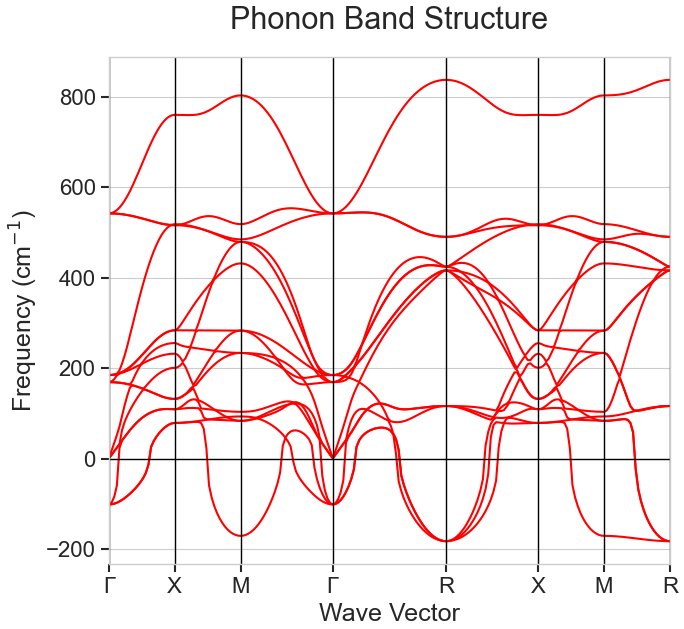
図2. 立方晶 CaTiO3 のフォノンバンド図。R点とM点において顕著な虚の振動数(ソフトモード)が確認できます。
計算の結果、ブリュアンゾーンの境界である R点 (1/2, 1/2, 1/2) および M点 (1/2, 1/2, 0) において、大きな虚の振動数が観測されました。これは、立方晶 CaTiO3 がポテンシャル曲面の「鞍点(サドル点)」に位置しており、特定の変形モードに対して自発的な対称性の破れが生じることを示唆しています。
3. 不安定モードの可視化と解析#
最も大きな不安定性を示したR点の振動モードを可視化したものを図3に示します。
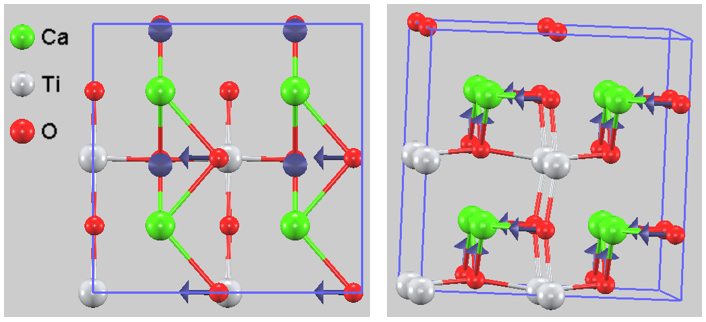
図3. R点における不安定モード(ソフトモード)の可視化(左:正面図、右:斜視図)。矢印は原子の変位方向を示します。酸素原子(赤)がTi原子(銀)を中心として回転しようとしている様子がわかります。
この図から、不安定性の起源は酸素八面体(TiO6)の回転運動 (Rotational instability)であることが明らかになりました [2] (関連する議論については [3] を参照)。特にR点のモードは、隣り合う八面体が互い違いに逆方向へ回転する「逆位相の回転(Anti-phase tilting)」に対応します。Caイオンのサイズが相対的に小さいため、大きな隙間を埋めるように酸素骨格が折れ曲がろうとする力が、この相転移の駆動力となっています。
4. 最適化された斜方晶構造と考察#
最後に、R点のソフトモードに沿って原子を微小に変位させた構造を作成し、セル形状(格子定数)を含む構造最適化を行いました。これにより、エネルギー的に最も安定な基底状態の構造が得られました(図4)。
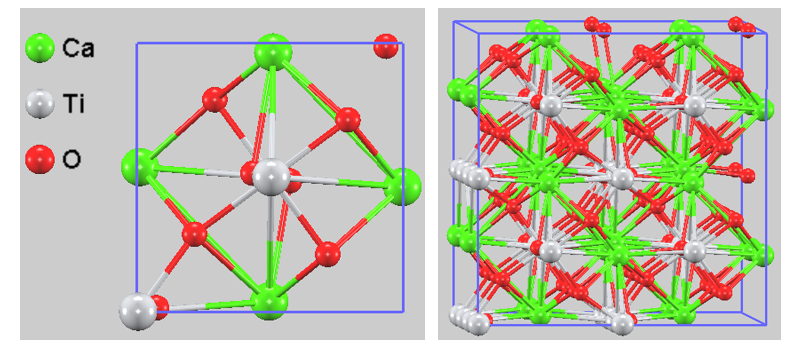
図4. 最適化された斜方晶 CaTiO3 の結晶構造。(左) 正面図、(右) 斜視図。立方晶では直線だった Ti-O-Ti 結合が折れ曲がり、酸素八面体が傾斜(Tilt)していることが明瞭に確認できます。
図4を見ると、理想的な立方晶ではすべての原子が直交するライン上に配置されていましたが、最適化後には酸素八面体(TiO6)が互い違いに大きく傾いていることがわかります。この構造歪みは、物理的には以下の2つの効果をもたらし、系を安定化させています。
- Caイオンの安定化: 立方晶の隙間はCaイオンにとって広すぎるため、八面体が傾くことで酸素原子がCaイオンに近づき、最適な配位環境(結合距離)が実現されました。
- パッキング効率の向上: 八面体の回転に伴い、不要な空隙が埋められ、単位胞全体の体積が収縮しました。
最終的に得られた格子定数を実験値 [4] と比較した結果を表2に示します。
表2. CaTiO3 (斜方晶) の格子定数の比較 (単位: Å)
| パラメータ | 本計算値 (GGA-PBE) | 実験値 [4] | 誤差 |
|---|---|---|---|
| a | 5.400 | 5.380 | +0.37% |
| b | 5.460 | 5.442 | +0.33% |
| c | 7.674 | 7.640 | +0.45% |
最適化された格子定数は、a ≠ b ≠ c/√2 という斜方晶(空間群 Pbnm)特有の異方性を正しく記述できており、定量的に見てもすべての軸で実験値との誤差が 0.5% 以下という良好な一致を示しました。これらの結果は、第一原理計算によるソフトモード解析が、複雑な酸化物の構造相転移メカニズムを原子レベルで解明する上で、非常に強力な手法であることを示唆しています。
まとめ#
本事例では、第一原理計算ソフトウェアAdvance/PHASEを用いて CaTiO3 の構造相転移メカニズムを解析しました。高温相である立方晶の状態方程式(EOS)計算では妥当な平衡体積が得られたものの、フォノン解析により酸素八面体の回転に対応する顕著なソフトモード(R点・M点)が発見され、構造が本質的に不安定であることが明らかになりました。この不安定モードに沿って原子を変位させ、セル形状を含めた構造最適化を行った結果、自発的に斜方晶への相転移が進行し、実験値を高精度に再現する安定構造が得られました。本手法は、温度や圧力に誘起される結晶構造変化や、未知の物質の安定相探索において強力なツールとなります。
本解析の詳細や、研究への適用可能性に関するご相談はこちら
お問い合わせ参考文献#
- S. Tariq, A. Ahmed, S. Saad, and S. Tariq, "Structural, electronic and elastic properties of the cubic CaTiO3 under pressure: A DFT study", AIP Advances 5, 077111 (2015).
- E. Cockayne and B. P. Burton, "Phonons and static dielectric constant in CaTiO3 from first principles", Phys. Rev. B 62, 3735 (2000).
- Ph. Ghosez, E. Cockayne, U. V. Waghmare, and K. M. Rabe, "Lattice dynamics of BaTiO3, PbTiO3, and PbZrO3: A comparative first-principles study", Phys. Rev. B 60, 836 (1999).
- S. Sasaki, C. T. Prewitt, J. D. Bass and W. A. Schulze, "Orthorhombic perovskite CaTiO3 and CdTiO3: Structure and space group", Acta Crystallogr. C 43, 1668 (1987).
関連ページ#
- 第一原理計算ソフトウェア Advance/PHASE
- 解析分野:ナノ・バイオ
- 産業分野:材料・化学