第一原理計算による物質の安定性評価 - bcc Tiの低温における不安定性 -#

新規機能性材料の探索において、対象とする物質が特定の結晶構造で安定に存在できるかどうかの検証は、極めて重要な課題です。構造の安定性は、単純なエネルギー計算（構造最適化）だけで判断することはできず、多角的な評価が求められます。本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、チタン(Ti)の高温相である体心立方(bcc)構造を対象に、その低温での安定性を評価します。これにより、物質の構造安定性を判断する上で第一原理計算がいかに有用であるかを示します。

Keywords: 第一原理計算, 物質の安定性, フォノン分散, 弾性定数, ボルンの安定性条件, bccチタン, 相転移, 格子振動

計算モデルと計算条件#

本計算は絶対零度における基底状態を評価するものであり、低温の実験条件に相当します。計算モデルとして、チタン(Ti)の体心立方(bcc)構造を対象としました。図1に、本計算で用いたbcc Tiの慣習セル（conventional cell）と基本セル（primitive cell）を示します。エネルギー-体積曲線と弾性定数の計算には慣習セルを、フォノン分散の計算には計算コストを考慮し基本セルをそれぞれ使用しました。

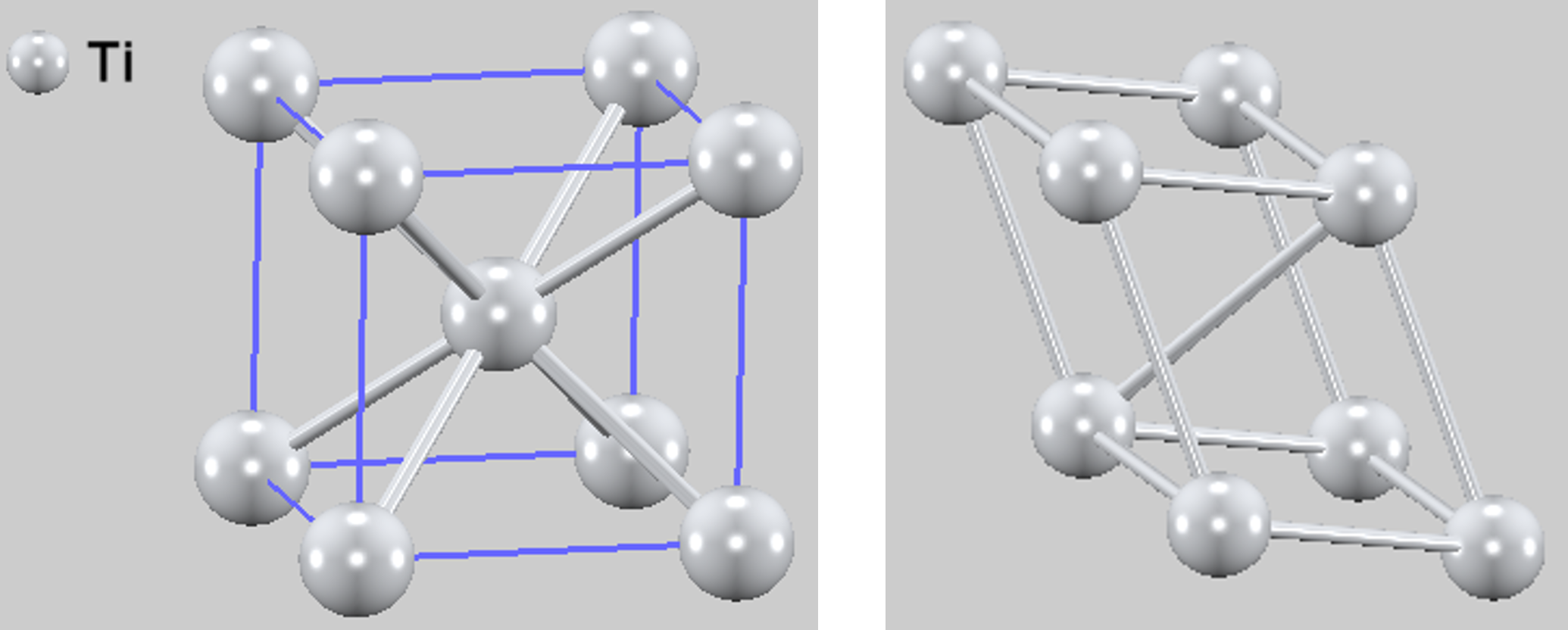
図1. bcc Tiの計算モデル。(左) 慣習セル、 (右) 基本セル

本解析で用いた主な計算条件は表1に示されています。

表1. 計算条件の概要

項目	設定
擬ポテンシャル	ウルトラソフト擬ポテンシャル (Tiの価電子配置：3s²3p⁶3d²4s²)
交換相関汎関数	GGA (PBE)
波動関数のカットオフエネルギー	エネルギー計算: 25 Rydberg ストレス計算: 40 Rydberg
k点サンプリング	慣習セル: 10x10x10 基本セル: 13x13x13

計算結果と考察#

ステップ1：エネルギー-体積曲線による評価#

まず、結晶の体積を等方的に変化させた際の全エネルギー変化（E-V曲線）を計算し、エネルギーが極小となる格子定数を求めました。図2に示すように、計算結果はきれいな曲線を描き、明確な極小点が存在します。この極小点における体積と曲率から、低温でのbcc Tiの格子定数は a = 3.2658 Å、体積弾性率は B = 108 GPaと算出されました。

E-V曲線に極小点が存在することは、その構造が体積変化に対しては安定であることを意味しますが、これだけでは物質が真に安定であると結論付けることはできません。

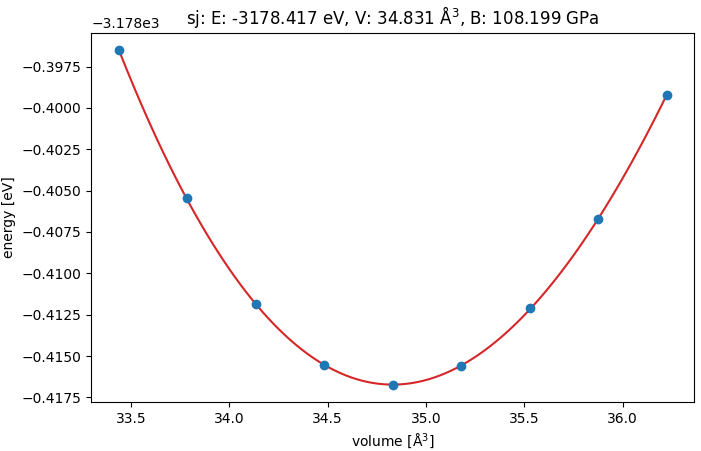
図2. bcc Tiのエネルギー-体積曲線。フィッティングにはsj (stabilized jellium)モデルを使用しました。

ステップ2：弾性定数による力学的安定性の評価#

次に、体積変化だけでなく、格子の形状変化（せん断ひずみなど）に対する安定性を評価するため、弾性定数を算出しました。結晶が力学的に安定であるためには、あらゆる微小なひずみに対してエネルギーが増加する必要があり、これはボルンの安定性条件 [1] として知られています。立方晶の場合、C₁₁ - C₁₂ > 0 および C₄₄ > 0 を満たすことが安定性の必要条件となります。

計算された弾性定数を表2に示します。本計算値は文献値 [2] と良い一致を示しています。しかし、C₁₁ (93.8 GPa) が C₁₂ (111.4 GPa) よりも小さく、C₁₁ - C₁₂ = -17.6 GPa < 0 となり、ボルンの安定性条件を満たさないことが明らかになりました。これは、bcc Tiが特定のせん断変形に対して抵抗できずに構造が崩壊することを示唆しており、力学的に不安定であることの明確な証拠です。

表2. bcc Tiの格子定数と弾性定数

	a (Å)	C₁₁ (GPa)	C₁₂ (GPa)	C₄₄ (GPa)
本計算値	3.2658	93.8	111.4	40.8
文献値 [2]	3.264	87.8	112.2	39.8

ステップ3：フォノン計算による動的安定性の評価#

最後に、原子の集団的な振動である格子振動（フォノン）を計算し、構造の動的な安定性を評価しました。構造が動的に安定である場合、全ての振動モードの周波数は実数となります。一方、不安定な構造では、周波数が虚数となるモード（虚数周波数モード）が出現します。

図3にbcc構造の第一ブリルアンゾーンと、フォノン分散の計算に用いた高対称k点経路（Γ-H-N-Γ-P-H-P-N）を示します。図4は、この経路上で計算したbcc Tiのフォノン分散曲線です。

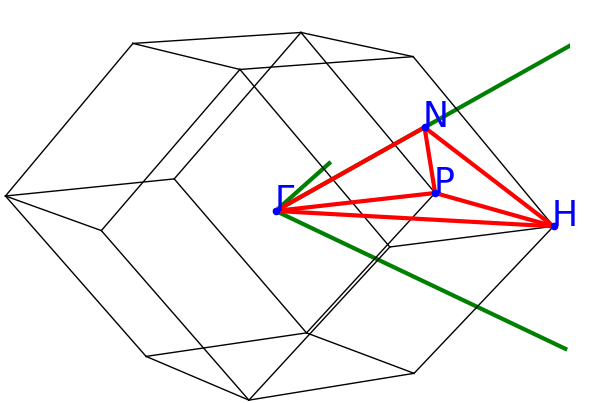
図3. bcc構造の第一ブリルアンゾーンとフォノン計算で用いた高対称k点経路

図4のフォノン分散曲線を見ると、N点やP点に向かう途中で周波数がゼロを通り抜け、負の値（グラフ上ではマイナスの周波数として表示）になっている領域がはっきりと確認できます。これが虚数の周波数を持つ不安定な振動モード（虚数振動モード）の存在を示しており、bcc Tiが格子振動に対して不安定（動的に不安定）であることを決定的に示しています。特に、N点での横波の不安定モードは、原子が(110)面を[1 $\bar{1}$ 0]方向に滑る変位に対応しており、これはbccからω（オメガ）相や六方最密充填構造(hcp)相への相転移経路の一部として知られています。この結果は、文献 [3] で示されているbcc Tiの格子不安定性の特徴とよく一致しています。

【NOTE】計算結果の解釈について

「N点での横波の不安定モード...」という記述は、フォノン計算の結果から導かれる物理的な結論であり、以下の専門的な背景と知見に基づいています。

N点：基本セル(primitive cell)の逆格子ベクトルを基底として定義されるブリルアンゾーン上の高対称点であり、その座標は(0, 0, 1/2)です。これは慣習セル(conventional cell)のデカルト座標系における波数ベクトル k = (2π/a)(1/2, 1/2, 0) に対応し、格子振動の波が[110]方向へ伝播していることを意味します。
横波 (Transverse mode)：フォノン計算では、各波数ベクトルkに対して動力学行列の固有値問題を解きます。その結果得られる固有ベクトルのうち、原子の変位方向が波数ベクトルkの方向と直交するものが横波モードです。本計算では、N点における不安定モードの固有ベクトルが[110]方向と直交していることが確認されました。
不安定モード：動力学行列の固有値は振動数の2乗(ω²)に対応します。この固有値が負の値を取ると、対応する振動数(ω)が虚数となります。これは、その変位に対して原子を元の位置に戻そうとする復元力が働かず、逆に変位を助長する力が働くことを示しており、構造がその変位に対して不安定であることを意味します。

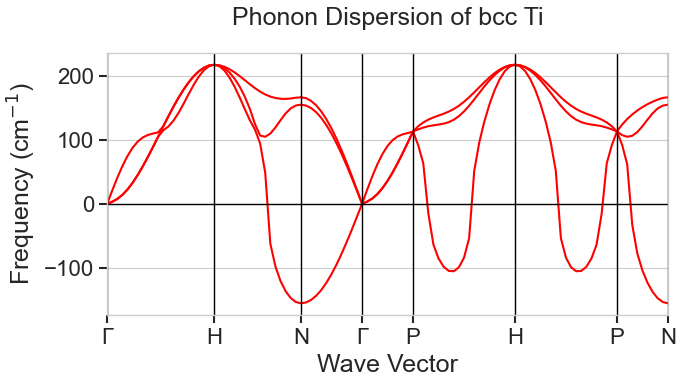
図4. bcc Tiのフォノン分散曲線。縦軸の負の領域は、格子が不安定であることを示す虚数周波数を表します。

まとめ#

本解析では、第一原理計算ソフトウェアAdvance/PHASEを用いて、高温相であるbcc Tiの低温における安定性を、E-V曲線、弾性定数、フォノン計算という3つの観点から多角的に評価しました。E-V曲線ではエネルギーの極小点が見られ、体積変化に対しては安定に見えましたが、弾性定数の計算からボルンの安定性条件(C₁₁-C₁₂ > 0)を満たさず、力学的に不安定であることが示されました。さらに、フォノン計算によって虚数振動モードの存在が確認され、構造が動的にも不安定であることが決定的となりました。これらの結果から、bcc Tiは低温では安定に存在しないと結論付けられます。このbcc構造の格子不安定性は、低温で安定なhcp構造へのマルテンサイト変態の起源と深く関連しています。本事例が示すように、物質の真の安定性を評価するには、単純なエネルギー計算だけでなく、力学的および動的安定性の多角的な検証が不可欠です。第一原理計算は、こうした評価を行うための強力なツールとなります。

参考文献#

F. Mouhat, and F. X. Coudert, "Necessary and sufficient elastic stability conditions in various crystal systems", Phys. Rev. B 90, 224104 (2014).
H. Ikehata, N. Nagasako, T. Furuta, A. Fukumoto, K. Miwa, and T. Saito, "First-principles calculations for development of low elastic modulus Ti alloys", Phys. Rev. B 70, 174113 (2004).
G. Grimvall, B. Magyari-Köpe, V. Ozoliņš, and K. A. Persson, "Lattice instabilities in metallic elements", Rev. Mod. Phys. 84, 945 (2012).