結晶対称性が支配する非線形光学応答：SHGとTHGの第一原理計算#

Advance/PHASE logo

レーザー光のような強い光を物質に入射した際に、入射光の周波数の整数倍の周波数を持つ光が発生する現象は「高調波発生」と呼ばれ、非線形光学効果の代表例です。特に、周波数が2倍になる第二次高調波発生（SHG）や3倍になる第三次高調波発生（THG）は、レーザーの波長変換技術などに応用される重要な現象です。これらの効果の発現は、物質の結晶構造が持つ「対称性」によって厳しく支配されます。本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、対照的な結晶対称性を持つ窒化アルミニウム（AlN）とシリコン（Si）の非線形光学応答を計算し、対称性と物性の相関を明らかにします。

Keywords: 第一原理計算, 非線形光学, 第二次高調波発生(SHG), 第三次高調波発生(THG), 結晶対称性, 空間反転対称性

計算手法：非線形感受率の第一原理計算#

物質の分極 $\vec{P}$ が、入射光の電場 $\vec{E}$ に対して非線形に応答する割合は、非線形感受率テンソル $\chi^{(n)}$ によって記述されます。

$P_i = \sum_j \chi^{(1)}_{ij} E_j + \sum_{jk} \chi^{(2)}_{ijk} E_j E_k + \sum_{jkl} \chi^{(3)}_{ijkl} E_j E_k E_l + \dots$

ここで、SHGは二次非線形感受率 $\chi^{(2)}$ に、THGは三次非線形感受率 $\chi^{(3)}$ に対応します。

Advance/PHASEでは、これらの感受率テンソルを、物質の電子バンド構造に基づいた量子力学的な摂動論から直接計算することができます。このアプローチにより、特定の材料がどの程度のSHG・THG応答を示すかを、実験に先立って高精度に予測することが可能です。

本計算では、交換相関汎関数としてGGA-PBE法を用いていますが、この手法は一般的に半導体のバンドギャップを実験値よりも過小評価する傾向があります。光学特性、特に共鳴ピークの位置はバンドギャップエネルギーに強く依存するため、この過小評価は結果の精度に直接影響します。そこで、この問題を補正するために「シザーオペレーター（Scissor Operator）」 [1, 2] と呼ばれる手法を適用しました。これは、計算されたバンド構造の伝導帯を一律にエネルギーシフトさせることで、バンドギャップを実験値に合わせる経験的な補正方法です。本解析では、AlNに対して 1.71 eV、Siに対して 0.60 eV のシザーオペレーターをそれぞれ適用し、より信頼性の高い光学スペクトルを得ています。

解析事例：AlNとSiにおける対称性の効果#

本解析では、代表的な半導体であるAlNとSiを取り上げます。この二つの物質は、非線形光学特性を決定づける上で重要な「空間反転対称性」に関して、正反対の性質を持っています。

結晶構造と空間反転対称性#

物質内のある点を中心に $\vec{r} \to -\vec{r}$ という反転操作を行ったとき、結晶構造が操作前と同一になる場合、その結晶は「空間反転対称性を持つ（中心対称）」と言います。

物質	結晶構造	空間反転対称性	光学応答
AlN (ウルツ鉱)	六方晶	無い (非中心対称)	$\chi^{(2)} \neq 0$ (SHG許容)
Si (ダイヤモンド)	立方晶	有る (中心対称)	$\chi^{(2)} = 0$ (SHG禁止)

上表に示すように、AlNのウルツ鉱構造は反転中心を持たないため、 $\chi^{(2)}$ がゼロにならずSHGが起こりえます。一方で、Siのダイヤモンド構造は反転中心を持つため、理論的にバルク（結晶内部）での $\chi^{(2)}$ は厳密にゼロとなり、SHGは禁止されます。その結果、Siで観測される最も低次の非線形効果は、 $\chi^{(3)}$ に由来するTHGとなります。

計算結果と考察#

AlNのSHGスペクトル#

図1に、AlNのSHGスペクトルのzzz成分 $\chi^{(2)}_{zzz}$ の計算結果を示します。虚部（赤線）はSHG過程におけるエネルギー吸収の大きさを表し、そのピークは物理的な共鳴現象に対応します。そして、このスペクトルはバンドギャップを境に二種類の共鳴が支配していると解釈できます。

まず、バンドギャップ以下のエネルギー領域では二光子共鳴が主役です。これは発生するSHG光のエネルギー（ $2\hbar\omega$ ）が電子遷移と共鳴する現象です。3.1 eV付近から応答が現れるのは、 $2\hbar\omega$ がバンドギャップ（約6.2 eV）に近づき「二光子吸収」が始まるためです。同様に、4.5 eV付近のピークも二光子共鳴であり、この場合はSHG光のエネルギー（ $2\hbar\omega \approx 9$ eV）が、より高エネルギーの電子遷移と強く共鳴していることを示しています。一方で、バンドギャップ以上のエネルギー領域では一光子共鳴が支配的になります。これは入射光のエネルギー（ $\hbar\omega$ ）自身が電子遷移と直接共鳴する現象です。7 eV付近に見られる非常に大きなピークは、まさに入射光が物質の電子遷移と強く共鳴していることに由来し、SHG現象を著しく増強させます。

本計算で得られたスペクトル形状と強度は、Rashkeevらが報告したAlNのSHGスペクトルの第一原理計算結果 [3] と類似しています。特に、スペクトルの虚部に注目すると、両者の計算ともに、低エネルギー側に負のピーク、高エネルギー側に正のピークを持つ特徴的な二重の共鳴構造を再現しています。

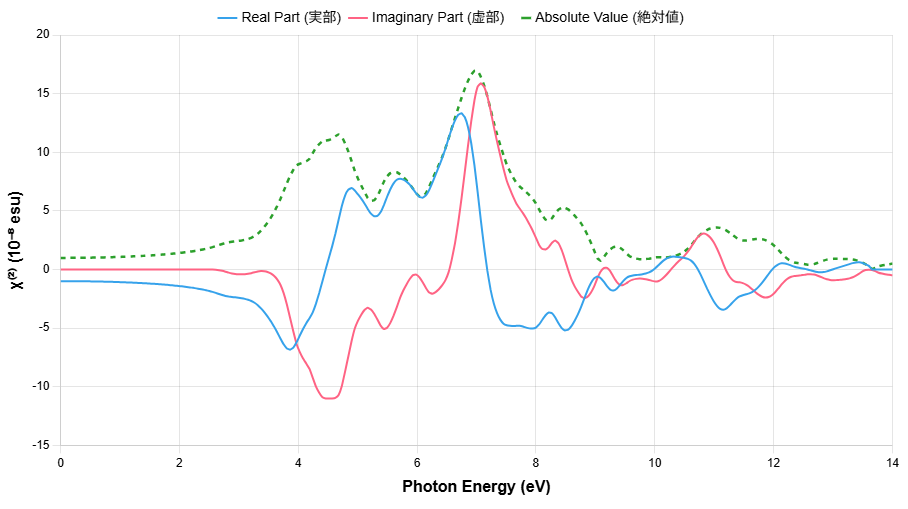
AlNのSHG感受率スペクトル（実部・虚部・絶対値）

図1. AlNの第二次非線形感受率 $\chi^{(2)}_{zzz}$ のスペクトル。実部（青）、虚部（赤）、絶対値（緑破線）をプロットしています。

SiのTHGスペクトル#

図2は、SiのTHGスペクトルのxxxx成分 $\chi^{(3)}_{xxxx}$ の計算結果です。前述の通り、Siは空間反転対称性を持つため $\chi^{(2)}$ はゼロになり、THGが主要な非線形応答となります。まず静的な値（ $\omega=0$ ）に着目すると、本計算による $\chi^{(3)}_{xxxx}(0)$ の値は $59.2\times10^{-12}$ esu となりました。これは、経験的タイトバインディング法による文献値 $48\times10^{-12}$ esu [4] と同程度のオーダーです。また、近年の別の第一原理計算（実時間発展法）による報告値は約 $25\times10^{-12}$ esu [5] です。これらの理論値は、実験値 $24\pm14\times10^{−12}$ esu と比較可能な範囲にあります [4]。

このスペクトルで最も顕著な特徴は、1.15 eV付近に見られる鋭いピークです。このピークは、発生するTHG光のエネルギー ( $3\hbar\omega$ ) が、Siの直接バンドギャップ（約3.4 eV）と共鳴する「三光子共鳴」に由来します。この共鳴条件を満たす入力光エネルギーは、理論的に $\hbar\omega \approx 3.4 \text{ eV} / 3 \approx 1.13 \text{ eV}$ と見積もられます。本計算で得られたピーク位置は、この理論的な予測と良い一致を示しています。このスペクトルの全体的な形状は、Attaccaliteらによる実時間発展法を用いた計算結果[5]とも一致しており、どちらの第一原理計算アプローチも三光子共鳴という同じ物理現象を正しく捉えていることを示しています。

一方で、Siの間接バンドギャップが約1.12 eVとこの値に非常に近接していますが、間接遷移は格子の振動（フォノン）を介した弱いプロセスです。そのため、 $\chi^{(3)}_{xxxx}$ スペクトルに現れるこのような強いピークは、運動量保存則を満たす直接遷移との共鳴によって支配されていると考えるのが物理的に自然です。通信波長帯である0.8 eV（1.55 $\mu$ m）付近では、共鳴から外れるため虚部がほぼゼロ（低損失）でありながら、有限の応答（絶対値）があるため、Siが低損失なTHGデバイスに応用できる可能性を示唆しています。

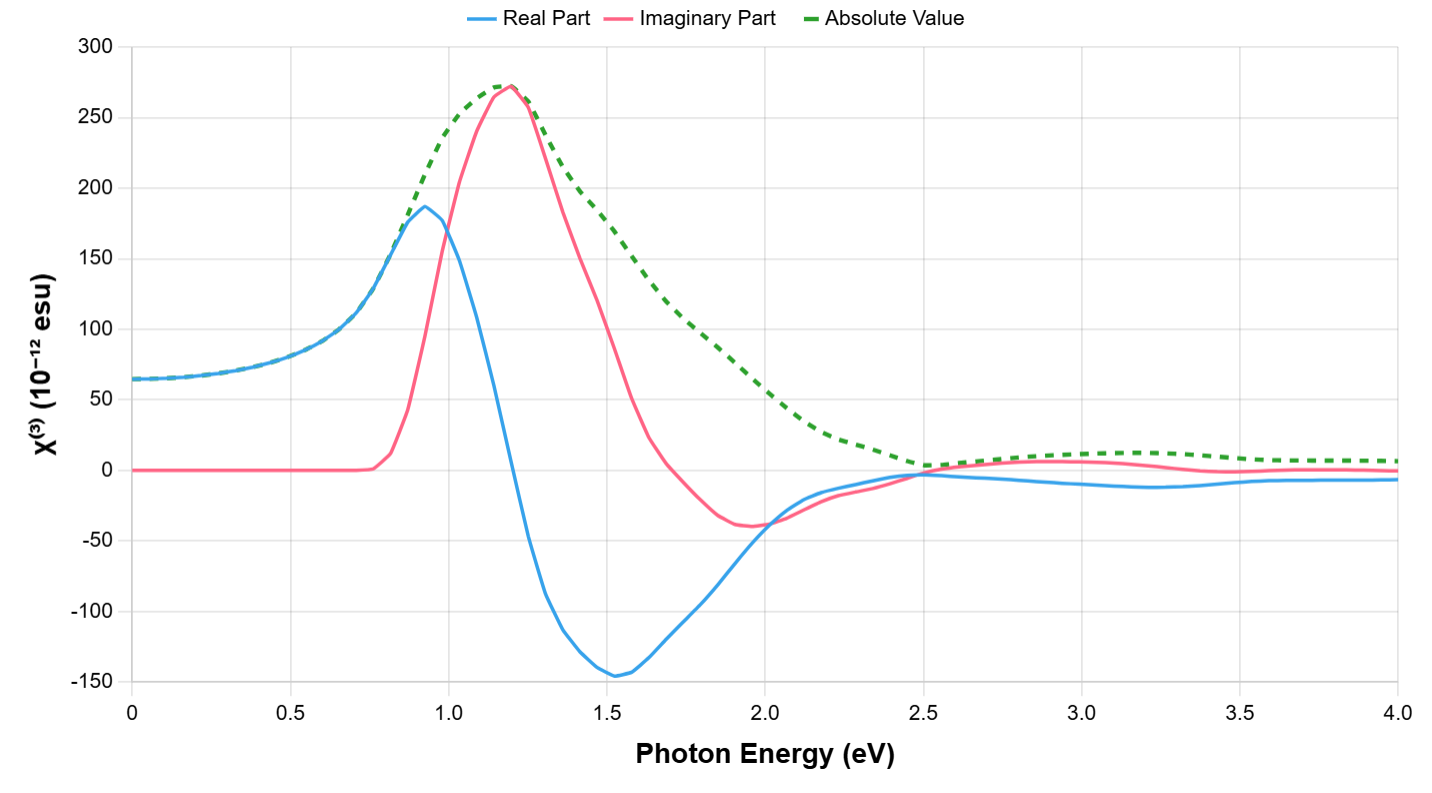
SiのTHG感受率スペクトル（実部・虚部・絶対値）

図2. Siの第三次非線形感受率 $\chi^{(3)}_{xxxx}$ のスペクトル。実部（青）、虚部（赤）、絶対値（緑破線）をプロットしています。

まとめ#

本解析では、第一原理計算ソフトウェアAdvance/PHASEを用いて、AlNとSiの非線形光学応答を計算しました。計算結果は、結晶の空間反転対称性の有無が、SHGやTHGといった非線形光学現象の発現を決定づけるという物理学の基本法則を明確に示しています。具体的には、空間反転対称性を持たないAlNではSHGが許容され、バンド構造を反映した鋭い共鳴ピークを持つスペクトルが得られました。これはAlNが紫外域の波長変換素子として有望であることを示唆します。一方、空間反転対称性を持つSiではSHGが禁止されるため、より高次の効果であるTHGが主要な応答となり、この結果はCMOSプロセスと親和性の高いシリコンフォトニクスにおける光信号の周波数操作の可能性を示します。

参考文献#

Z. H. Levine and D. C. Allan, "Linear optical response in silicon and germanium including self-energy effects", Phys. Rev. Lett. 63, 1719 (1989).
F. Nastos, B. Olejnik, K. Schwarz, and J. E. Sipe, "Scissors implementation within length-gauge formulations of the frequency-dependent nonlinear optical response of semiconductors", Phys. Rev. B 72, 045223 (2005).
S. N. Rashkeev, W. R. L. Lambrecht, and B. Segall, "Efficient ab initio method for the calculation of frequency-dependent second-order optical response in semiconductors", Phys. Rev. B 57, 3905 (1998).
D. J. Moss, E. Ghahramani, J. E. Sipe, and H. M. Van Driel, "Band-structure calculation of dispersion and anisotropy in χ(3) for third-harmonic generation in Si, Ge, and GaAs", Phys. Rev. B 41, 1542 (1990).
C. Attaccalite and M. Grüning, "Nonlinear optics from an ab initio approach by means of the dynamical berry phase: Application to second-and third-harmonic generation in semiconductors", Phys. Rev. B 88, 235113 (2013).