Advance/PHASEを用いたイオン拡散経路のシミュレーション#

第一原理計算を用いて、物質中の原子の拡散経路を Nudged Elastic Band 法を用いてシミュレーションした事例を紹介します。具体的には、グラファイト中にインターカレートされたリチウム原子の拡散過程をシミュレーションしました。第一原理計算ソフトウェア Advance/PHASE Ver.4.0 では、中間状態の構造を最適化するための時間積分法として Fast Inertial Relaxation Engine アルゴリズムを導入したので、その有効性を紹介します。

Keywords: 第一原理計算, 最小エネルギー経路計算, Nudged Elastic Band法, 障壁エネルギー, Li-GIC, リチウム拡散

Nudged Elastic Band法#

化学反応機構や物質の原子レベルでの拡散機構を理解するためには、その反応や拡散の経路を解析し、始状態と終状態、そして遷移状態の構造とエネルギーなどを調べることが有効です。始状態と終状態が決まっているときに、その間を結ぶ最小エネルギー経路と鞍点(遷移状態)を求める方法のひとつに、 Nudged Elastic Band (NEB) 法[1-3]があります。

NEB法では、始点と終点の間にいくつかの中間状態（イメージ）を仮定し、それらがバネで繋がっているかのようにして全体の構造を最適化します。初期の中間状態は、始点と終点を単純に分割して作ることが一般的です。しかし、このNEB 法には、中間状態同士が強く影響し合うため、最適化計算に時間がかかるという課題がありました。そこで、この問題を解決するために、Fast Inertial Relaxation Engine (FIRE) アルゴリズムという手法が開発されました。FIREアルゴリズムは、エネルギーの状態に応じて計算の進め方を調整することで、構造最適化を大幅に高速化でき、 Advance/PHASE にも採用されています。

計算結果#

リチウムイオン 2 次電池の負極に用いられているリチウムがインターカレートされたグラファイト (Li-GIC) 内でのリチウムの拡散経路のシミュレーションを例に、NEB 法を用いた計算結果を紹介します。

Li-GICの結晶構造#

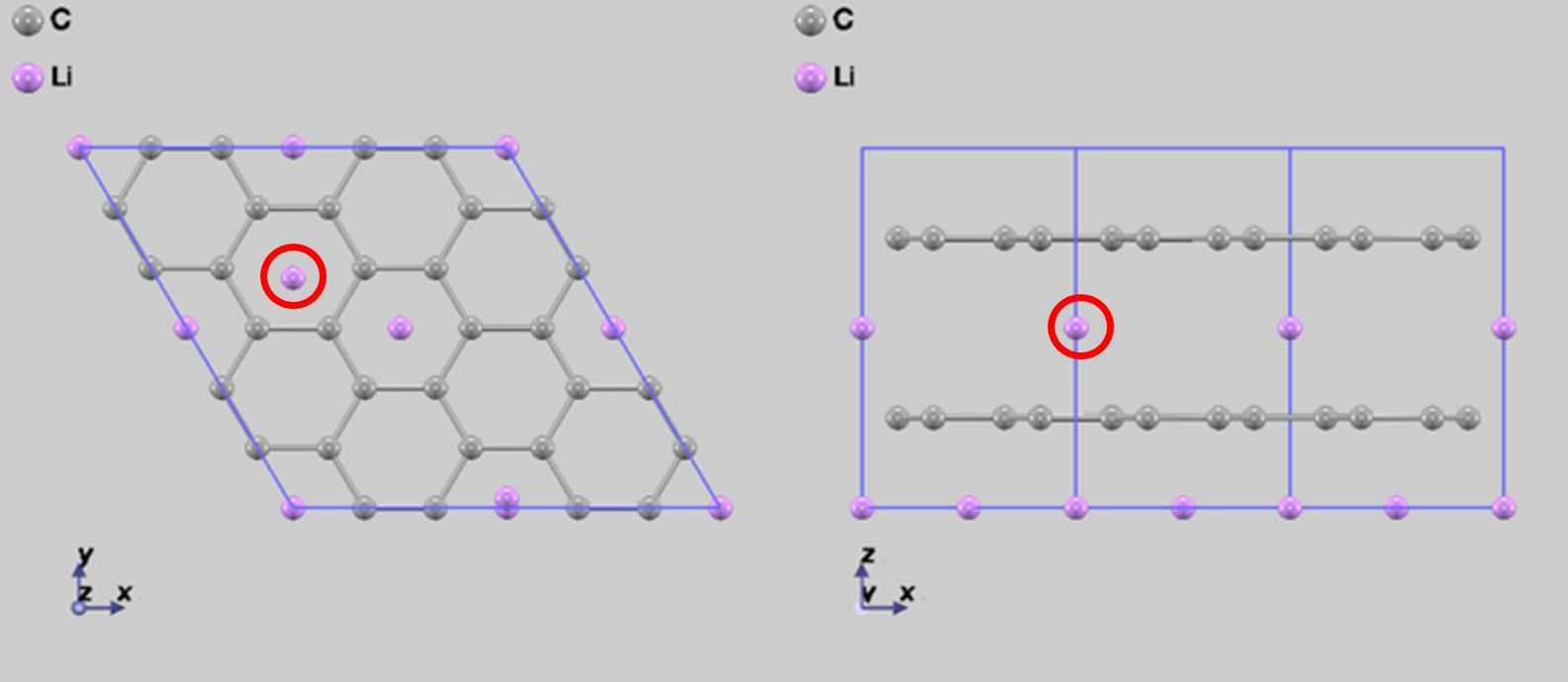
Li-GIC には、インターカレートされているリチウムの量に応じて、様々な構造があります。その中でも、リチウムが高濃度でインターカレートされている $LiC_6$ を用いてシミュレーションを行いました。図1 に、 $LiC_6$ の構造を示します。図1 のユニットセルで拡散のシミュレーションを行うと、ユニットセルには 1 個のリチウム原子が含まれているだけなので、周期境界条件を用いた計算では、全てのリチウム原子が同じ方向に同時に移動する計算を行うことになります。これでは、拡散の素過程をシミュレーションしていることにはならないので、ユニットセルを 2×2×2 に拡張した計算セルでシミュレーションを行います。この計算セル(詳細は後述の図2 参照)を用いると、炭素膜間には 4 個のリチウム原子が存在し、リチウム原子層は 2 層存在します。

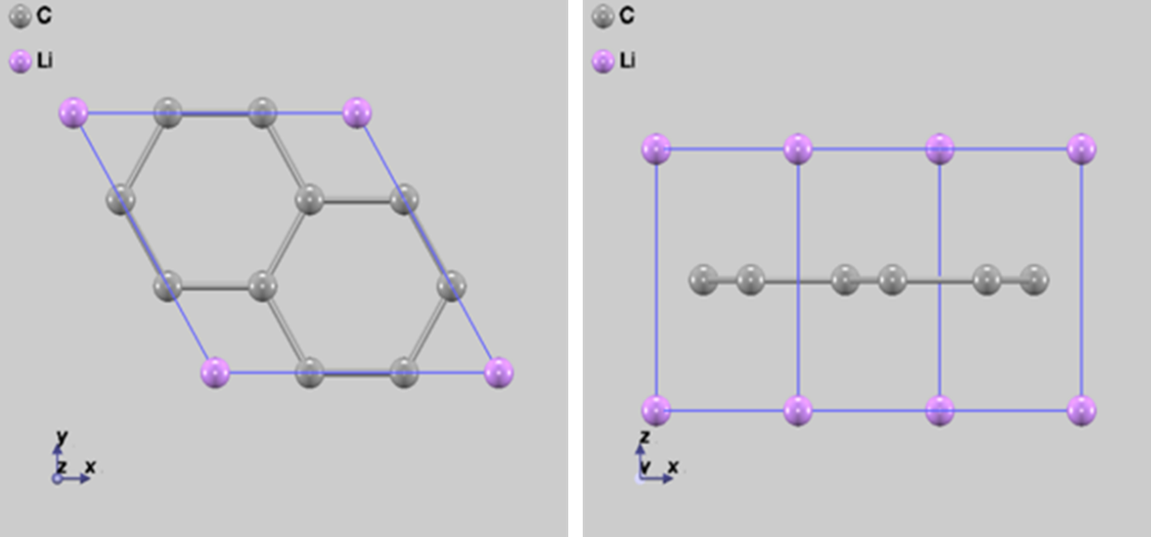
図1　 $LiC_6$ の結晶構造（ユニットセルで表示）

拡散経路のシミュレーション#

完全系での拡散#

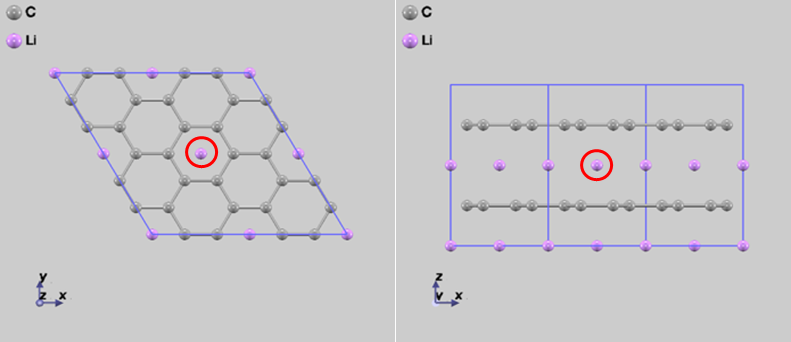
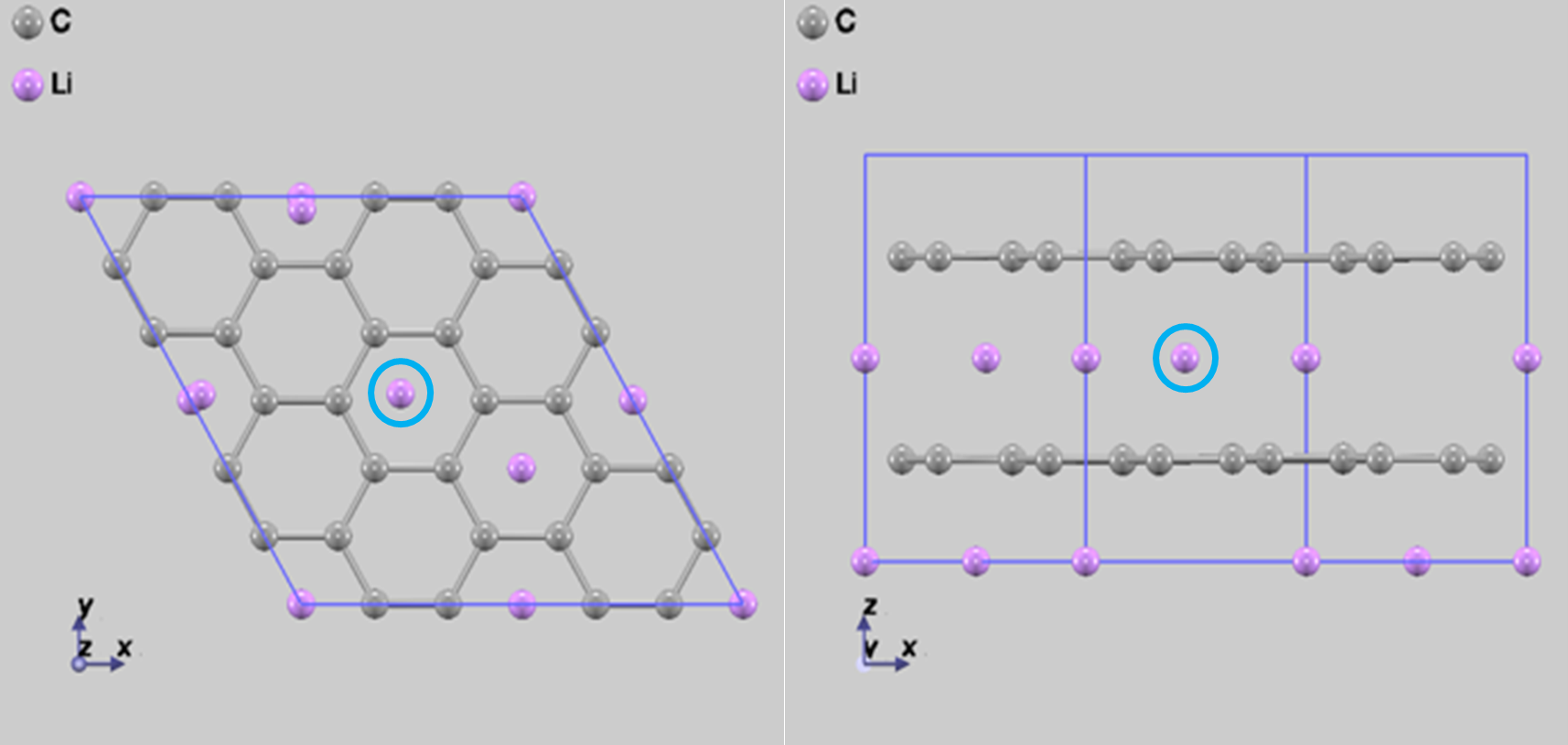
はじめに、NEB 法を用いて、図2(a)から(b)に赤丸で囲んだリチウム原子が拡散するときのシミュレーションを行いました。この経路を拡散 Step1 とします。このとき、通常の MD アルゴリズムを用いたところ、拡散経路が求まるまでに 1738 回の構造に対する繰り返し計算が必要でした。経路に沿ったエネルギー変化を図3 に示します。

(a)

(b)

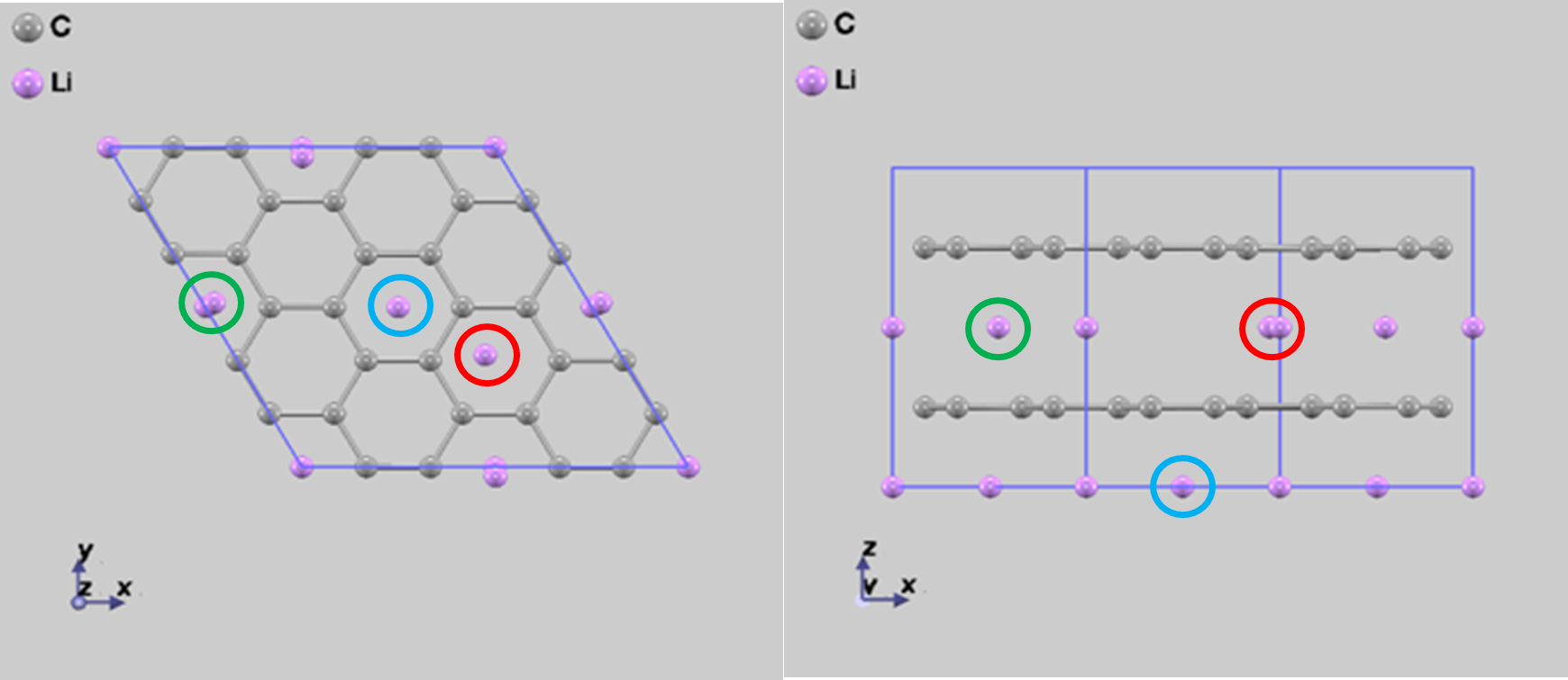
図2　完全系での拡散シミュレーション Step1。始状態(a)から終状態(b)へ赤丸で囲んだリチウム原子が拡散している

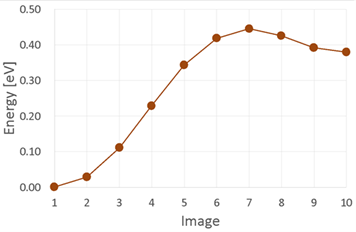
図3　図2の始状態から終状態に拡散したときのエネルギープロファイル

この拡散では、図3の経路上の7番目の中間状態（Image 7）で最大エネルギーとなり、このエネルギーを拡散の活性化障壁エネルギーと考えます。その際のエネルギー値は 0.44 eV でした。遷移状態は、図4の構造のときであることが分かり、これはグラファイトの炭素-炭素結合の上を通過した直後でした。

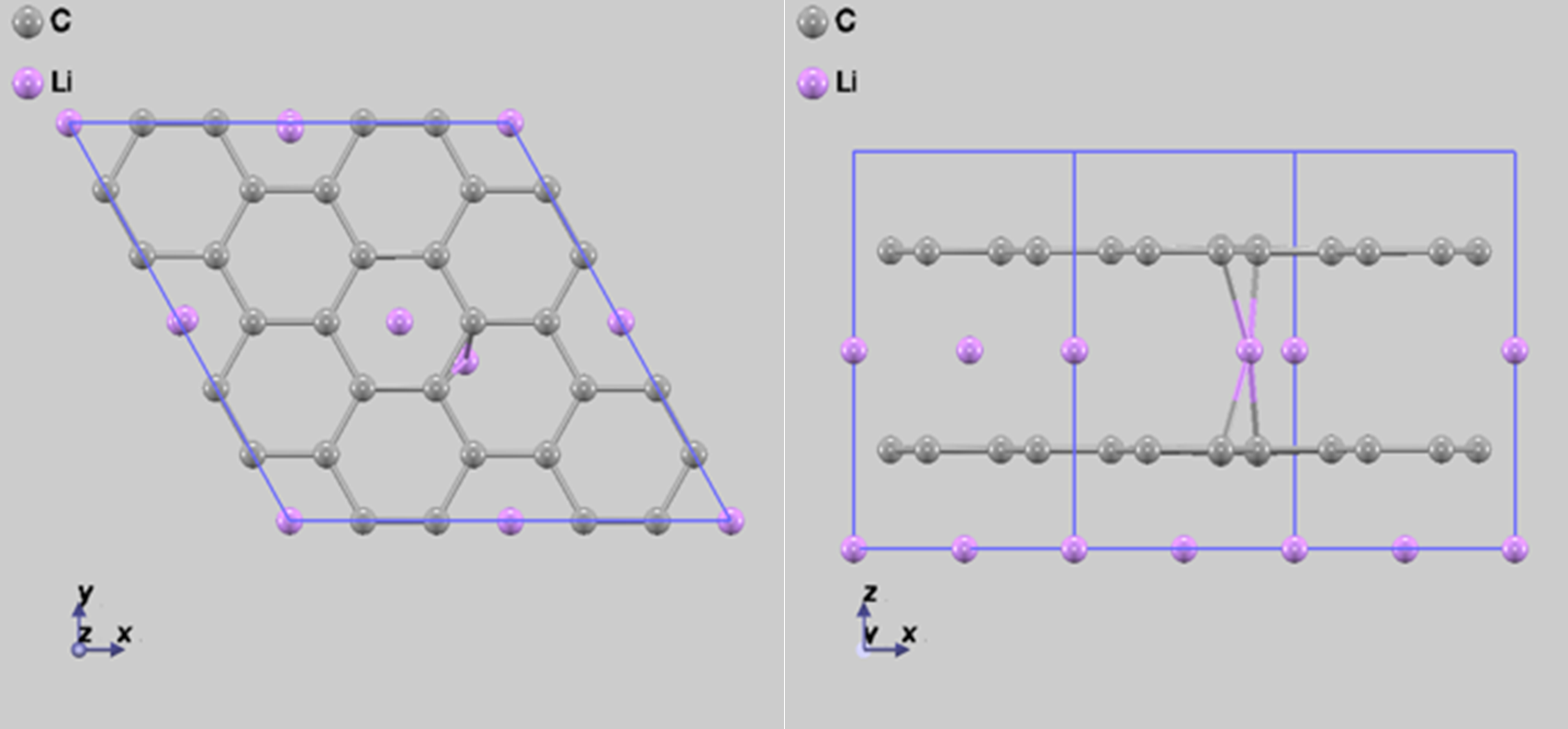
図4　拡散経路step 1の遷移状態の構造

(a)Step2-1

(b)Step2-2

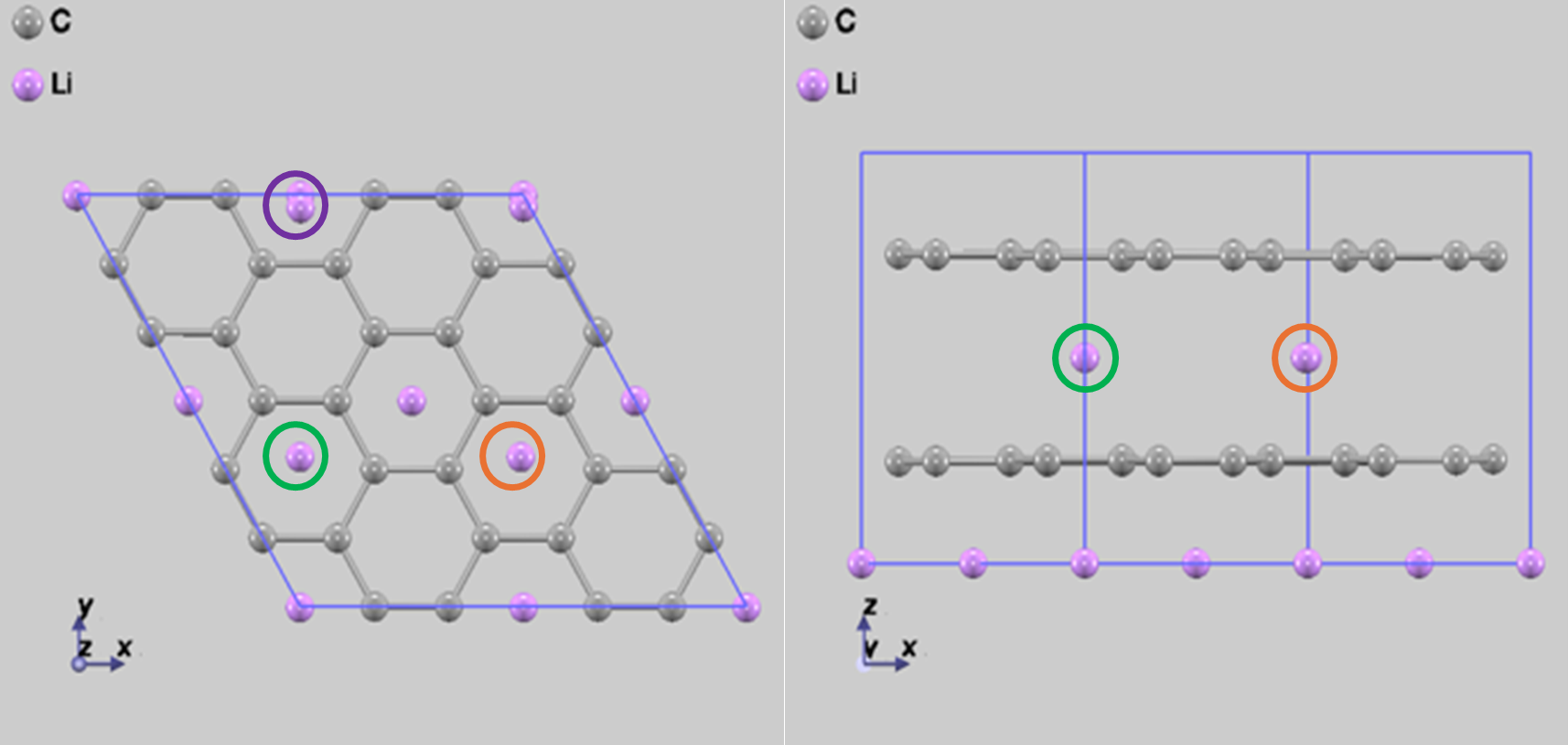
図5　拡散経路Step 2の２つの終状態

次に、拡散 Step1 の終状態（図2(b)）を始状態とし、図5のいずれかの構造を終状態となる2つの経路 (Step 2) を考えました。1つ目の拡散 (Step 2-1) は、下層のリチウム原子（図5(a)の青丸で囲んだ原子）が炭素の六員環を通り抜けて、Step1 の拡散で空いたサイトに移動する経路です。2つ目の拡散(Step 2-2)は、図2 (b)の緑丸で囲んだリチウム原子が移動する経路です。図6に経路に沿ったエネルギー変化を示します。ここから、Step 2-1（図6(a)のプロファイル）は非常に活性化障壁エネルギーが大きい (7.90 eV) ためこのような拡散は起こらず、また、遷移状態は炭素の六員環を通り抜けるときになると考えられます。Step 2-2 における活性化障壁エネルギーは、0.20 eV となっており、拡散が一度起こると、次の拡散は起こりやすくなることが分かります。この拡散経路の計算にも通常の MD アルゴリズムを用いており、3000 回以上の繰り返し計算が必要でした。

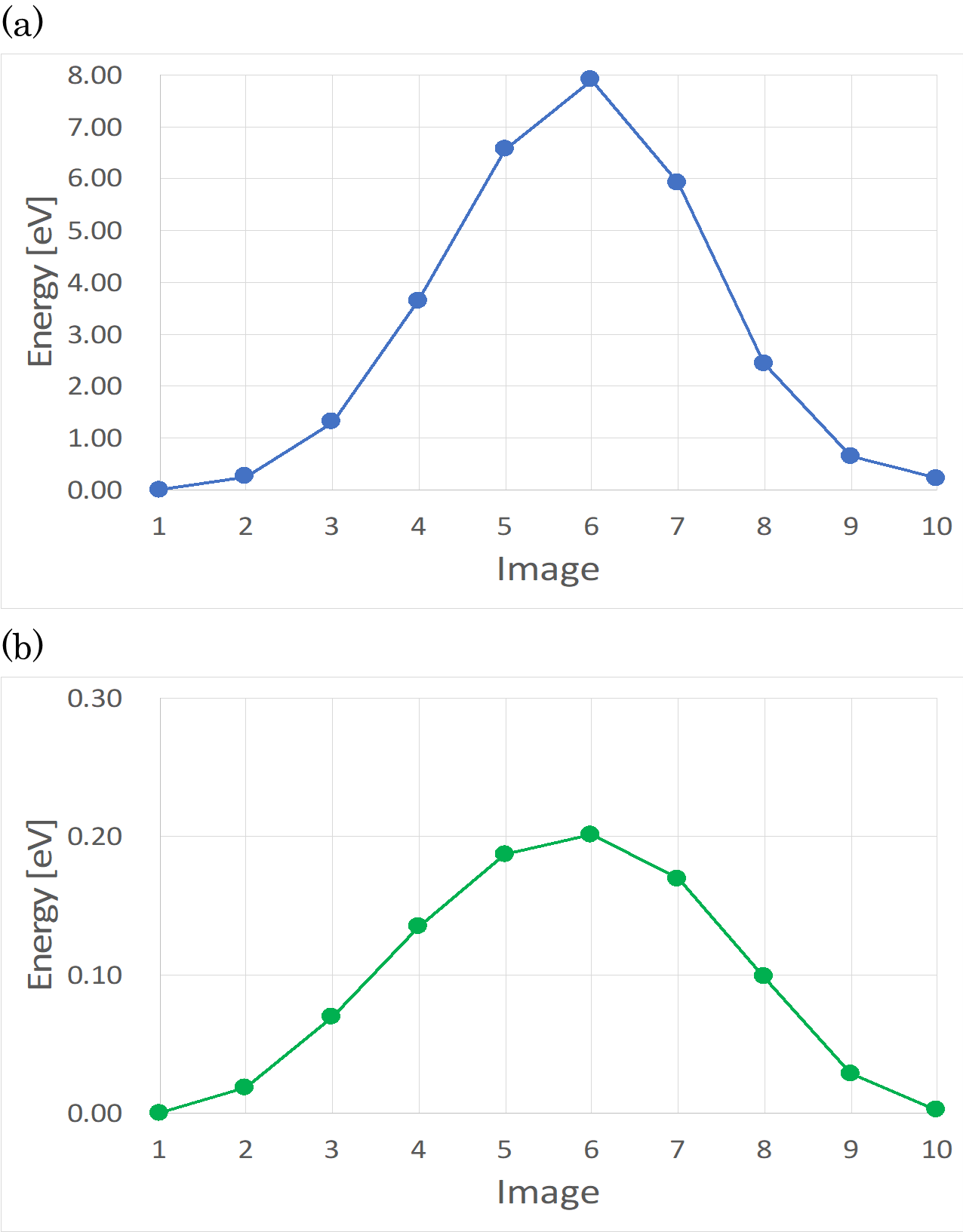
図6　図2(b)から図5に拡散したときのエネルギープロファイル

FIREアルゴリズムを用いた計算結果#

これまでのシミュレーションで、NEB 法を用いた計算では、中間状態の収束までに多くの繰り返し計算が必要であることが分かりました。そこで、次のステップからは、構造緩和計算を大幅に加速する FIRE アルゴリズムを用いて計算を行います。

考慮した経路は、図5(b)から図7になる拡散によるものです(Step 3-1、Step 3-2)。FIRE アルゴリズムを用いると、65 回の繰り返し計算で収束しました。これは、通常のMDを用いた場合の 1/50 以下です。このことから、新しく導入したFIREアルゴリズムが中間状態のシミュレーションに対して有効であることが明らかになりました。

この拡散経路に沿ったエネルギープロファイルを図8に示します。Step 3-1 では活性化障壁エネルギーは 0.23 eV となり、Step 3-2 では 0.20 eV となりました。Step 3 では、Step 3-2 の方が起こりやすく、その終状態のエネルギーも図7(b)の構造の方が低くなると分かりました。

(a)Step3-1

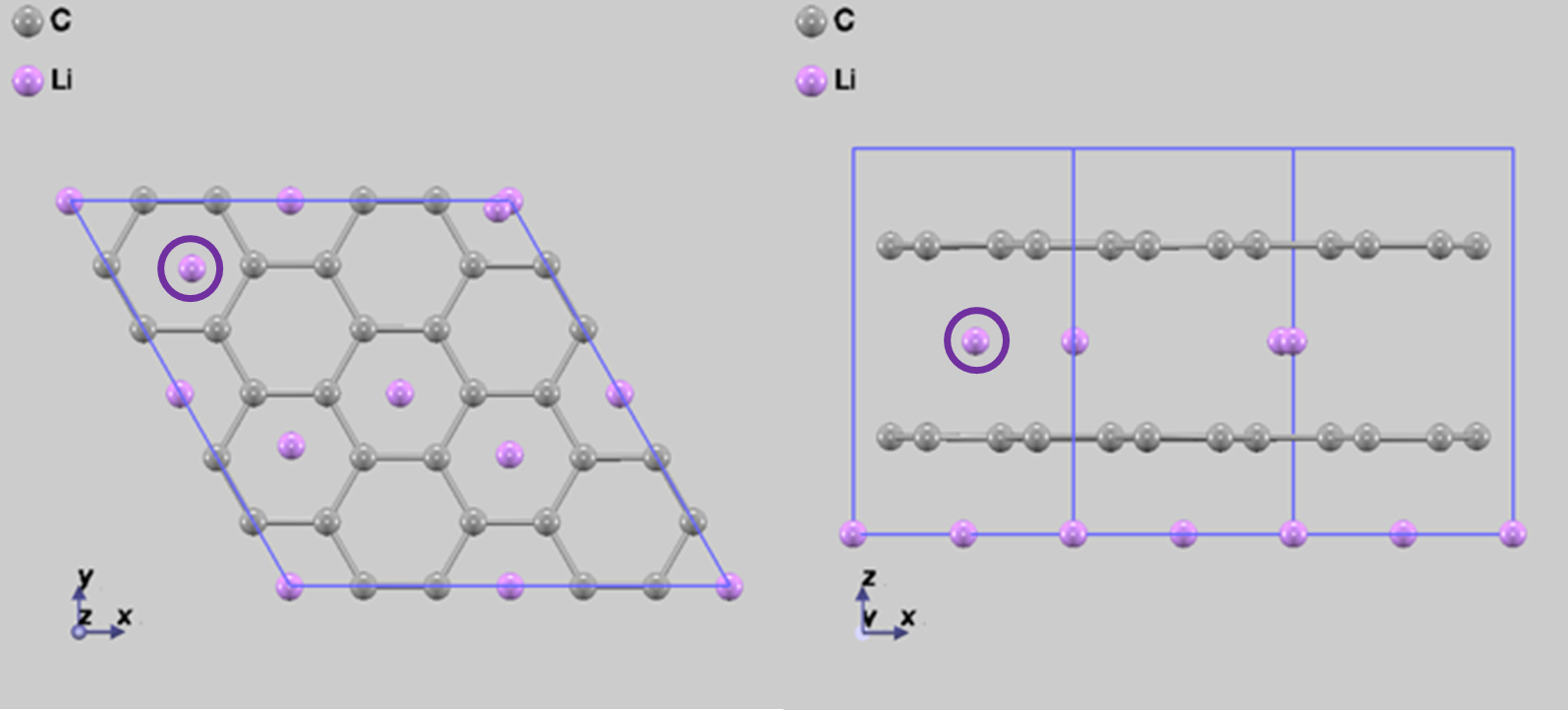
(b)Step3-2

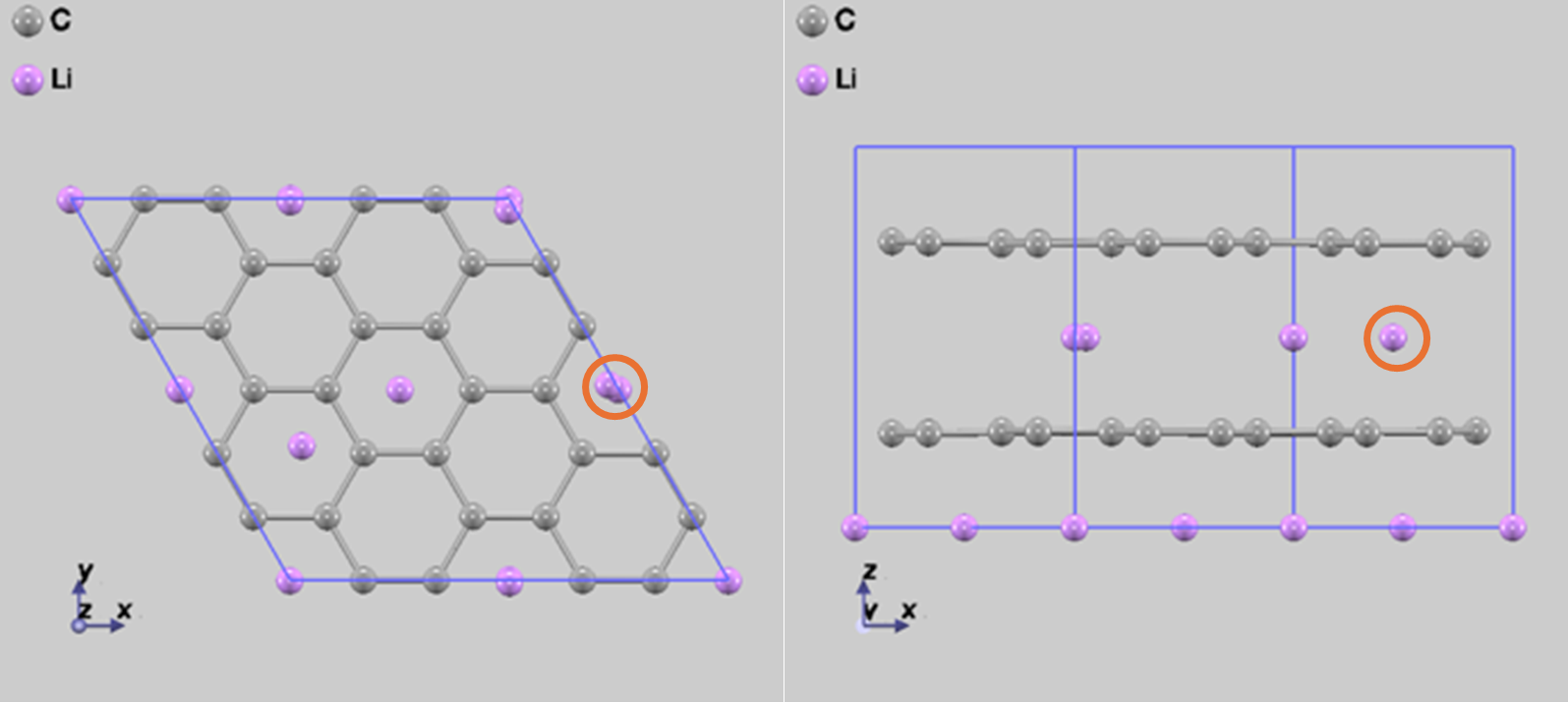
図7　拡散経路Step 3の２つの終状態

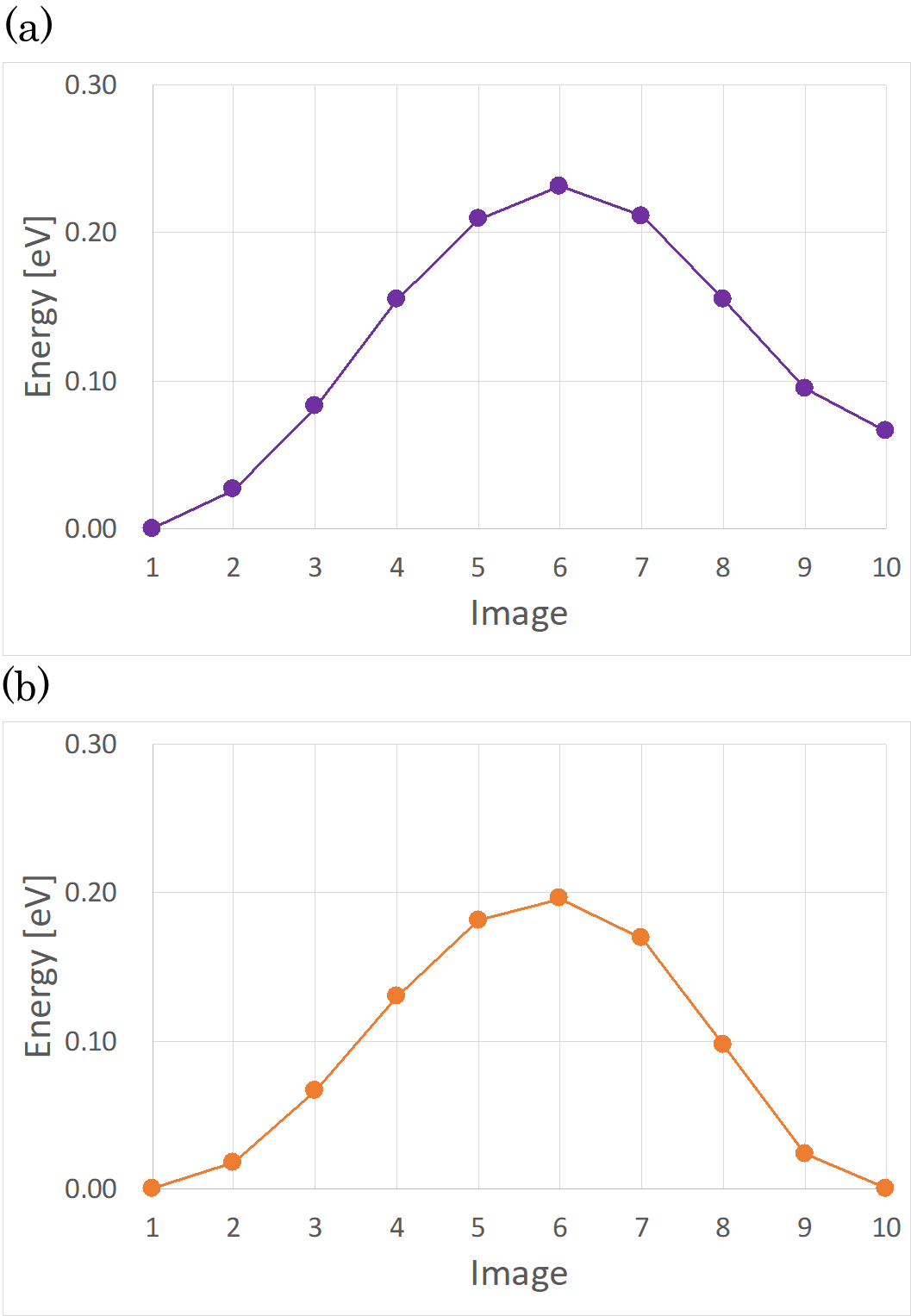
図8　図5(b)から図7に拡散したときのエネルギープロファイル

欠陥系での拡散#

$LiC_6$ では、完全系でもリチウム原子の間に隙間があるので、拡散することが可能です。しかし、リチウム原子がわずかに少なくなっている場合、拡散がどのように変化するかを知ることも重要です。別のグラファイト層間から炭素原子層を通り抜ける拡散が起こらないことは既に分かっているので、層内での拡散だけを考慮しました。そこで、NEB法を用いて図9(a) → (b) → (c)の順に拡散するときのシミュレーションを行いました。このとき、図9(a)の点線の黒丸で囲んだ一のリチウム原子が抜けており（リチウム原子空孔）、赤丸のリチウム原子が拡散しているとしました。この拡散により、リチウム原子とリチウム原子空孔が入れ替わったことになります。

図10に拡散経路に沿ったエネルギープロファイルを示します。この拡散経路での活性化障壁エネルギーは、(a) → (b)は 0.37 eV となり、(b) → (c)は 0.17 eV となりました。

(a)

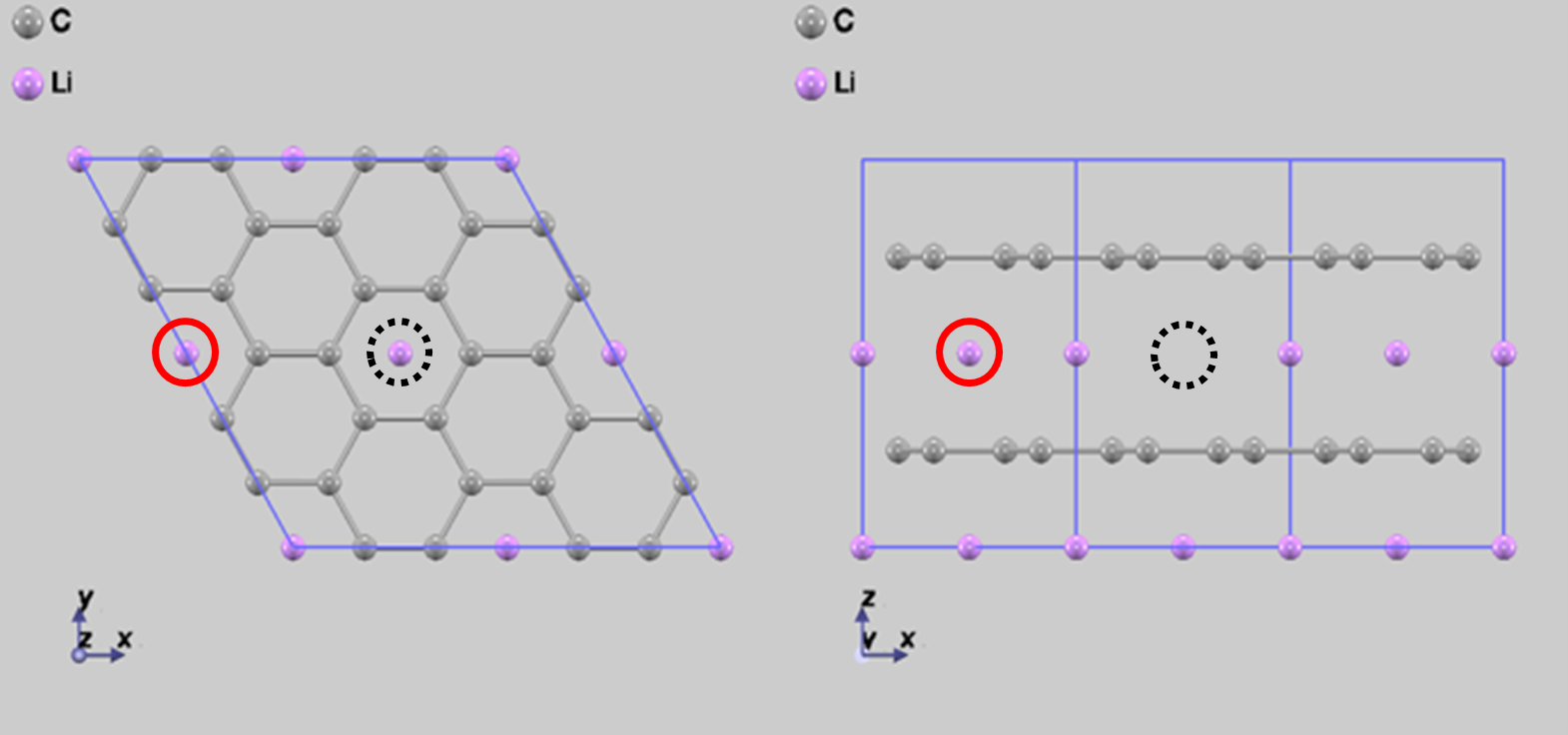
(b)

(c)

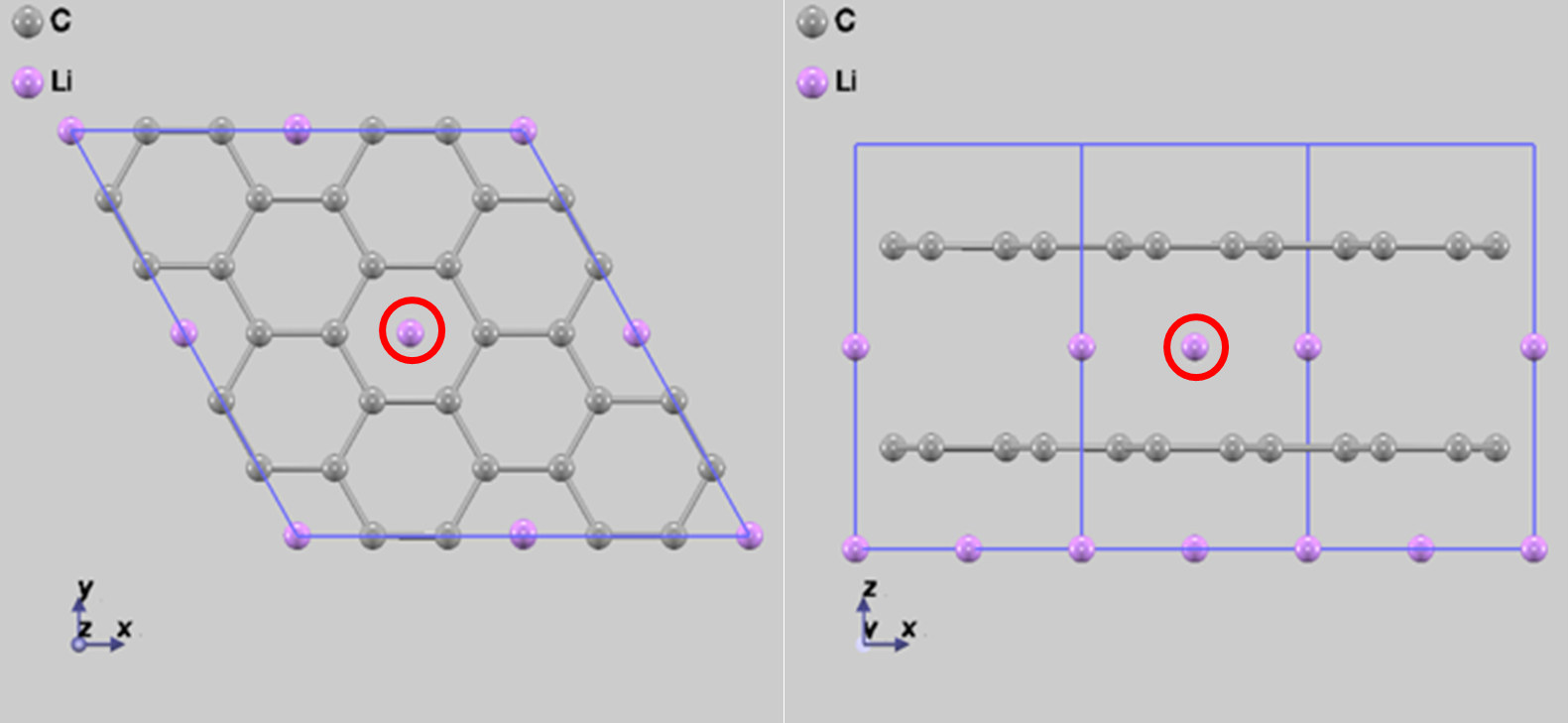
図9　1個のリチウム原子が抜けている((a)の黒点線の丸の位置)ときの拡散経路

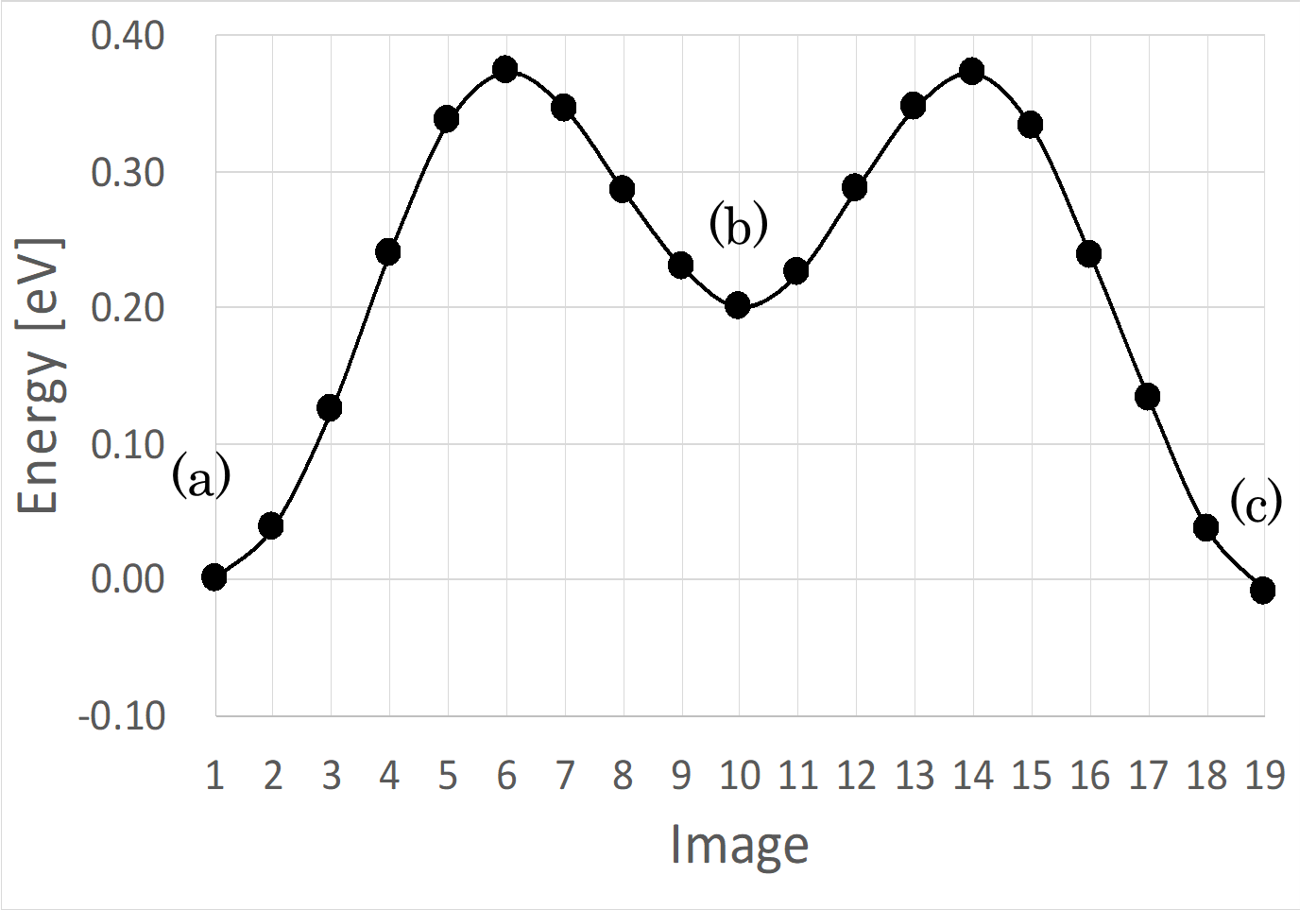
図10　1個のリチウム原子が抜けているときの拡散経路に沿ったエネルギープロファイル

(a)→(b)の活性化障壁エネルギーは、完全系での拡散の Step1 よりも小さい（完全系の Step1 では、0.44eV）という結果になりました。(b)→(c)の活性化障壁エネルギーが(a)→(b)よりも小さいのは、(b)のエネルギーが(a)や(c)よりも0.20 eV高い状態となっているためです。これらのことから、欠陥があるとリチウム原子の拡散が起こりやすくなることが分かります。この結果は、 Toyoura らの結果 [4] と一致します。

一方で、完全系にリチウム原子空孔を作るには、空孔生成エネルギー E(vac) =0.24 eV が必要となります。これらのことから、リチウム原子空孔が存在するとリチウム原子の拡散が起こりやすくなること（活性化障壁エネルギーが0.07 eV 低くなる）と、それ以上のエネルギーが空孔生成のために必要となることが分かります。

今回実施したNEB法での拡散経路の最適化には、FIRE アルゴリズムを用いました。繰り返しの回数は、(a) → (b)が 98 回、(b) → (c)が 86 回でした。

まとめ#

第一原理計算ソフトウェア Advance/PHASE を用いて、Li-GIC 中で Li 原子が拡散するときの経路に沿ったエネルギープロファイルと遷移状態をシミュレーションしました。

Li-GIC の中で、高濃度でリチウム原子がインターカレートされている $LiC_6$ で拡散経路を求めると、グラファイトの炭素層を通り抜ける拡散では、拡散障壁エネルギーが 7.90 eV となり、このような拡散はほとんど起こらないことが分かりました。続いて起こる拡散では、拡散障壁エネルギーが 0.20 eV 程度となり、リチウム原子が拡散し始めると、次のステップからは障壁エネルギーが小さくなることが分かりました。一連の経路に沿ったエネルギープロファイルを図11に示します。

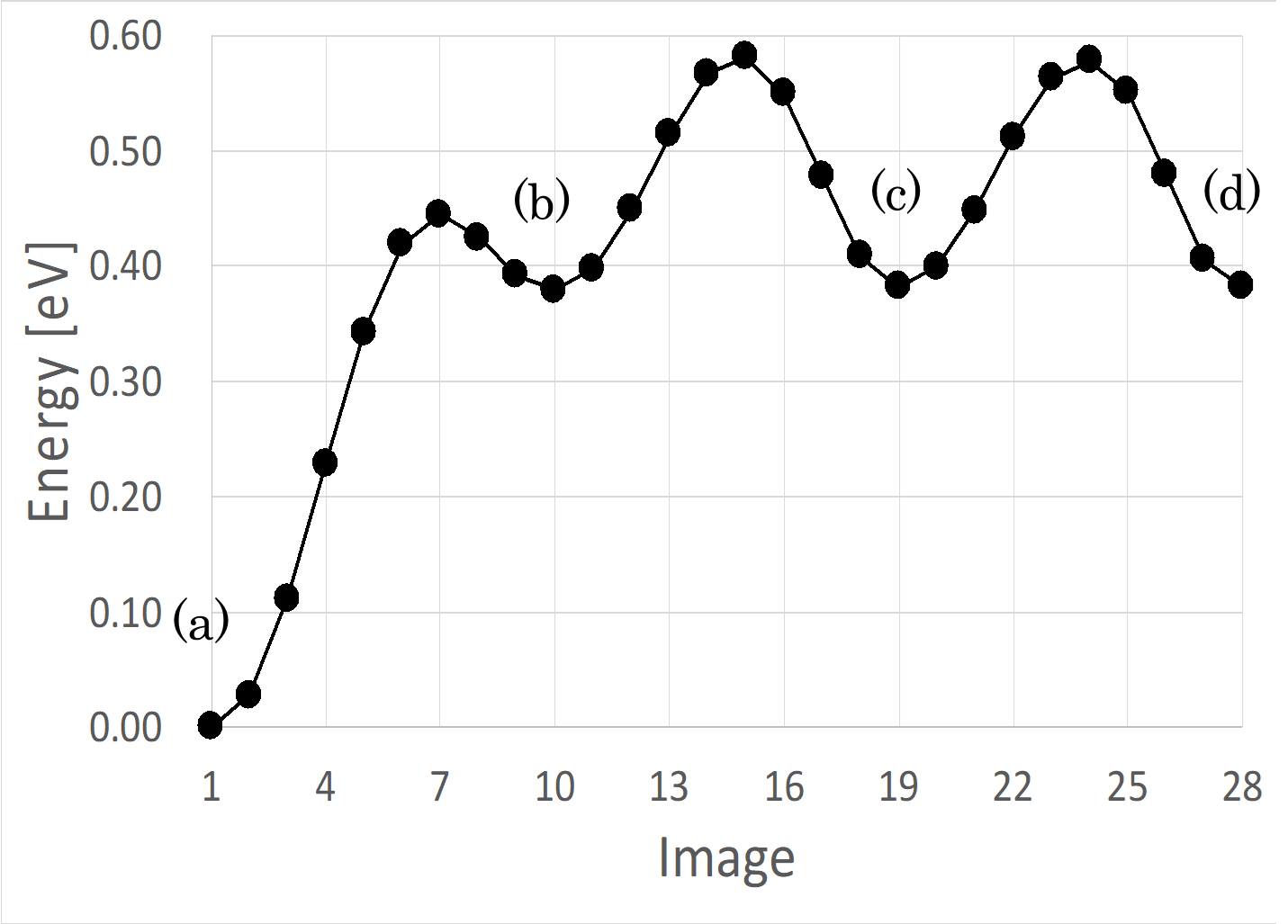
図11　欠陥がない(完全系) Li-GIC ( $LiC_6$ )でのリチウム原子が拡散するときのエネルギープロファイル

次に、1個のリチウム原子が抜けている場合での拡散を調べると、原子空孔がない場合と比較して、低い障壁エネルギーとなることが分かりました。しかし、原子空孔を作るには0.24 eVのエネルギーが必要であることも分かりました。また遷移状態は、すべての場合で、リチウム原子が炭素原子間結合の上を通過した直後（図4）であることが分かりました。

完全系の場合（図11）では(b) → (c)に移動するよりも(b) → (a)に戻る移動の方が低い活性化障壁となり、活性化障壁を越える確率がボルツマン分布に従うとすると、(b) → (a)に戻る移動の方が起こりやすい事象であることが分かります。一方で、欠陥系の場合では(b) → (a)の移動も(b) → (c)の移動もほぼ同じ活性化障壁となり（図10）、同じ確率で起こる事象であることが分かります。

NEB法による最小エネルギー経路探索において、これまでのアルゴリズム(quenched MD など)を用いた最適化では、1600〜3000 回の繰り返し計算が必要でした。NEB 法を用いた場合では、各構造に強い相関があるため構造の最適化が難しくなります。しかし、Advance/PHASE Ver.4.0 で新たに導入した FIRE アルゴリズムを用いると、60〜100 回程度の繰り返し計算で拡散経路を見つけることができます。

参考文献#

H. Jónsson, G. Mills, K. W. Jacobsen, “Classical and Quantum Dynamics in Condensed Phase Simulations”, edited by B. J. Berne, G. Ciccotti, D. F. Coker, World Scientific, Singapore, 1998, p. 385.
G. Henkelman, P. Uberuaga, H. Jónsson, J. Chem. Phys. 113 (2000) 9901.
G. Henkelman, H. Jónsson, J. Chem. Phys. 113 (2000) 9978.
K. Toyoura, Y. Koyama, A. Kuwabara, F.Oba, I. Tanak, Phys. Rev. B 78 (2008)214303.