表面官能基がMXeneの電子状態に与える影響の第一原理計算#

MXeneは、MAX相と呼ばれる導電性層状セラミックス材料から合成される二次元(2D)の遷移金属炭化物・窒化物であり、そのユニークな物理的・化学的特性から次世代の電子デバイスやエネルギー貯蔵材料として注目されています。MAX相は、一般式がMn+1AXn(M: 遷移金属, A: 主に第13族または第14族のAサイト元素, X: 炭素/窒素)で表され、金属的なM-X層と、化学的に反応しやすいA原子の層が交互に積層した結晶構造を持っています。このA層を選択的にエッチング(除去)することで、二次元シートであるMXeneが得られます。MXeneの特性は、合成過程で導入される表面官能基によって大きく変化することが知られています。本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、代表的なMXeneであるTi3C2に-O, -F, -OHの3種類の官能基を導入した際の構造、電子状態、仕事関数の変化を評価し、官能基が物性に与える影響を明らかにします。
Keywords: 第一原理計算, DFTシミュレーション, MXene, Ti3C2, 表面官能基, 構造最適化, 状態密度, バンド構造, 仕事関数
計算モデルと計算条件#
本計算では、MXeneの合成実験 [1] に対応して、Ti3C2の表面を-O, -F, -OHの官能基で終端した3種類のモデル、Ti3C2O2, Ti3C2F2, Ti3C2(OH)2を作成しました。文献 [2, 3] に基づき、官能基が最もエネルギー的に安定となる配置(Ti層のすぐ下にあるC原子に囲まれたホローサイト)を採用しました。図1~3に、構造最適化後の各モデルの原子配列を示します。
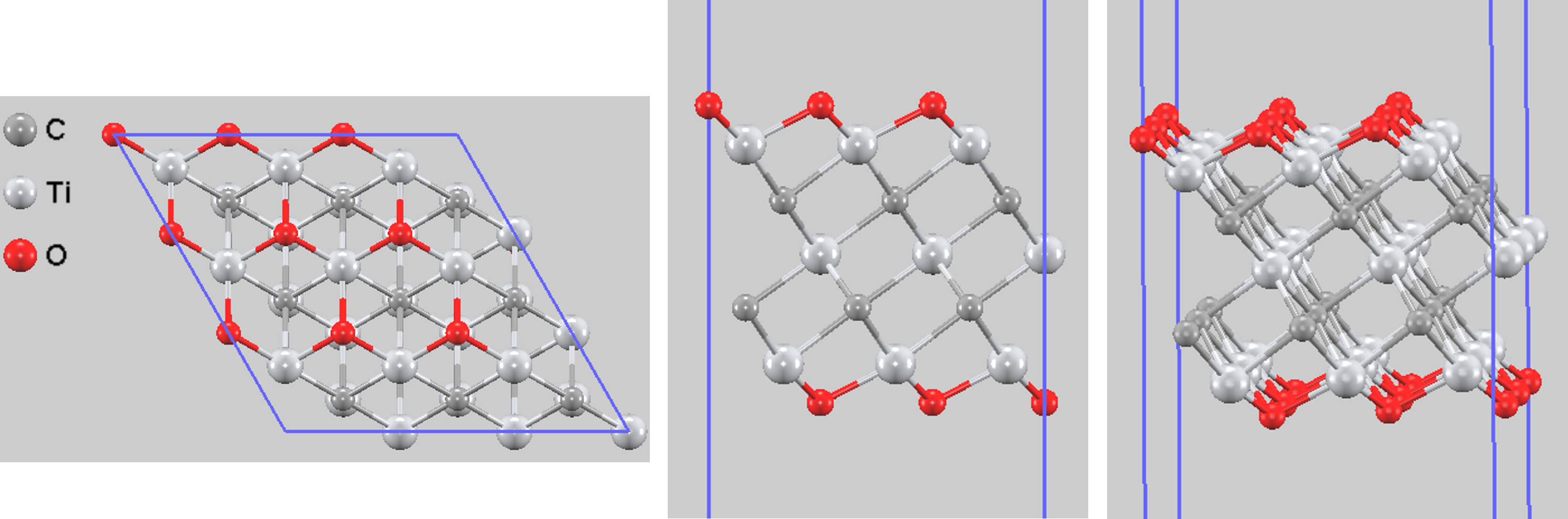
図1. 最適化されたTi3C2O2の構造。(左から)上面図、側面図、斜視図。
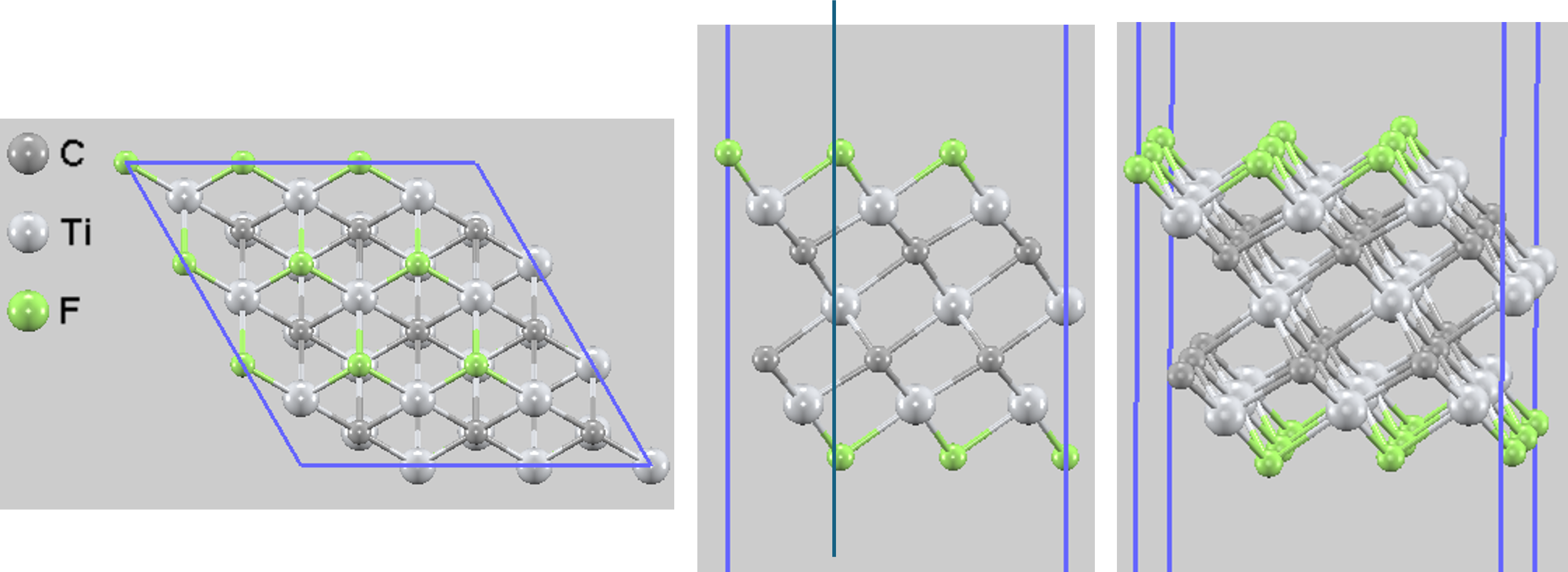
図2. 最適化されたTi3C2F2の構造。(左から)上面図、側面図、斜視図。
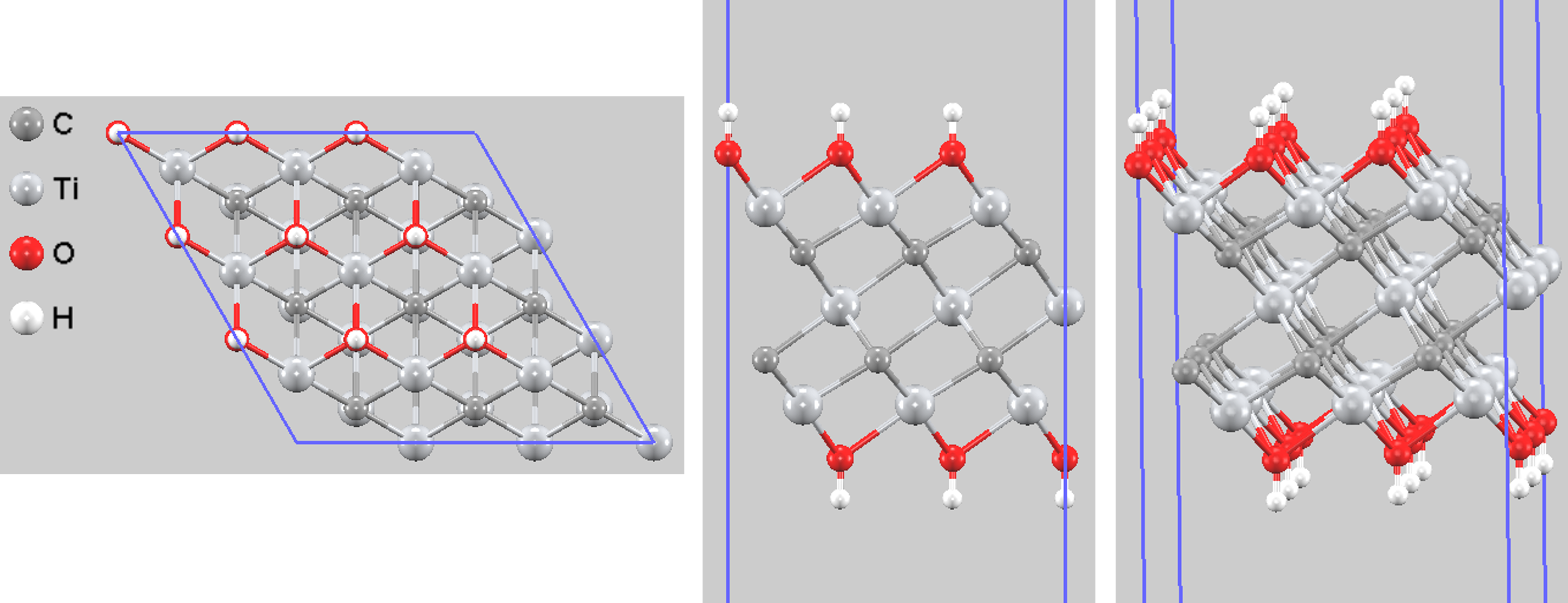
図3. 最適化されたTi3C2(OH)2の構造。(左から)上面図、側面図、斜視図。
本解析で用いた主な計算条件は表1に示されています。
表1. 計算条件の概要
| 項目 | 設定 |
|---|---|
| 擬ポテンシャル | ウルトラソフト擬ポテンシャル (H: ノルム保存) |
| 交換相関汎関数 | GGA (PBE) |
| 波動関数のカットオフエネルギー | 25 Rydberg (約340 eV) |
| k点サンプリング (SCF計算) | 10x10x1 |
| 真空層の厚さ | 15 Å以上 |
計算結果と考察#
格子定数の最適化#
各モデルについて、全エネルギーが最小となるように格子定数aを最適化しました(図4)。
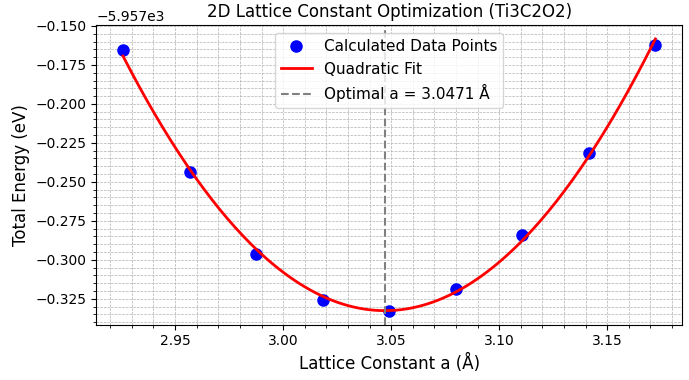
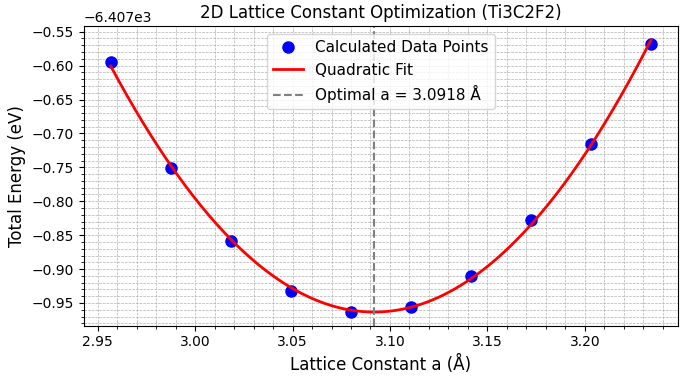
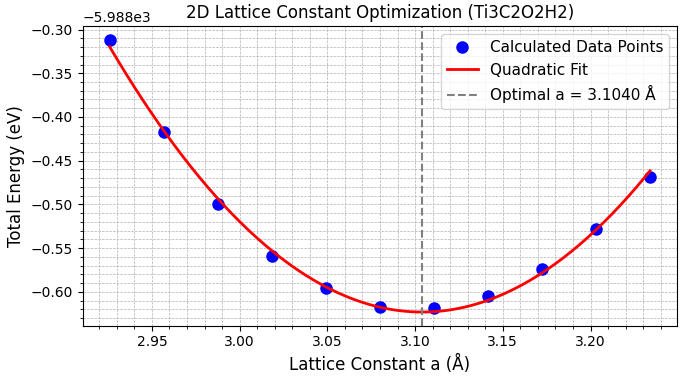
図4. (上から)Ti3C2O2、Ti3C2F2、Ti3C2(OH)2の格子定数最適化。全エネルギー(縦軸)と格子定数a(横軸)の関係をプロットし、二次関数でフィッティングして最適値を決定しました。縦軸の値に対して、軸の上端にオフセットが示されています。
得られた最適格子定数を文献値と比較したものを表2に示します。本計算で得られた格子定数の序列(Ti3C2O2 < Ti3C2F2 < Ti3C2(OH)2)および各値は、文献 [2] と非常によい一致を示しており、本計算の妥当性が確認できます。Ti-O結合は共有結合性が強くTi原子を引き付けるため格子定数が最も小さくなり、一方で-OH基は立体的要因から最も大きな格子定数を示すと考えられます。
表2. 最適化された格子定数a (Å)の比較
| モデル | 本計算値 | 文献値 [2] |
|---|---|---|
| Ti3C2O2 | 3.047 | 3.039 |
| Ti3C2F2 | 3.092 | 3.076 |
| Ti3C2(OH)2 | 3.104 | 3.086 |
電子状態#
計算されたバンド構造と状態密度(DOS)から、-O, -F, -OHで終端されたTi3C2はいずれもフェルミ準位にバンドが交差しており、金属的な性質を示すことがわかりました。図5に代表としてTi3C2F2の計算結果を示します。DOSの形状は、より高精度なハイブリッド汎関数(HSE06)を用いた文献 [3] の結果と定性的に良い一致を示しており、電子状態の主要な特徴を捉えられていることが確認できます。
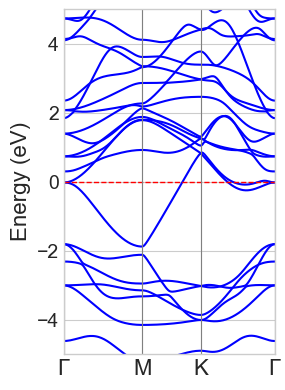
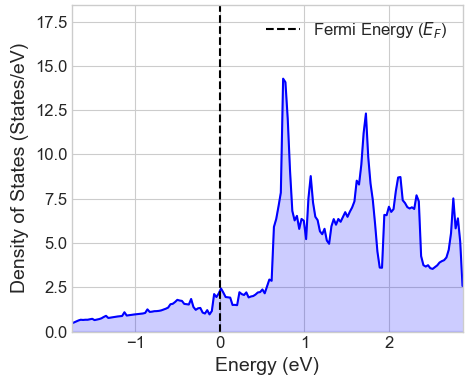
図5. Ti3C2F2のバンド構造(左)と状態密度(右)。
仕事関数#
仕事関数(Φ)は、真空準位(Evac)とフェルミ準位(EF)のエネルギー差(Φ = Evac - EF)として定義されます。本解析では、スラブモデルの表面におけるポテンシャルプロファイルを正確に計算できるESM法(Effective Screening Medium法)を用いて仕事関数を算出しました(図6)。
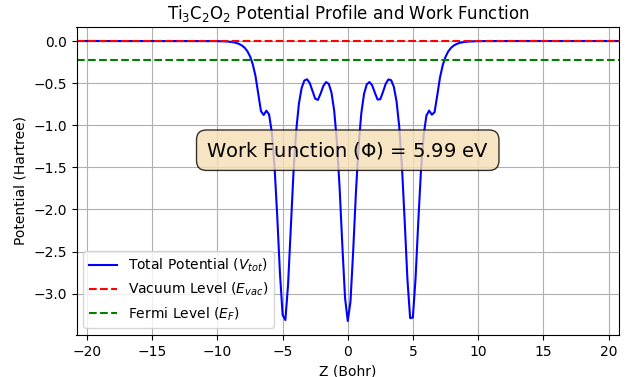
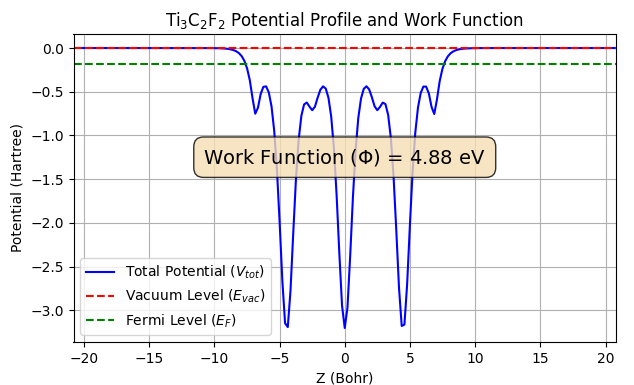
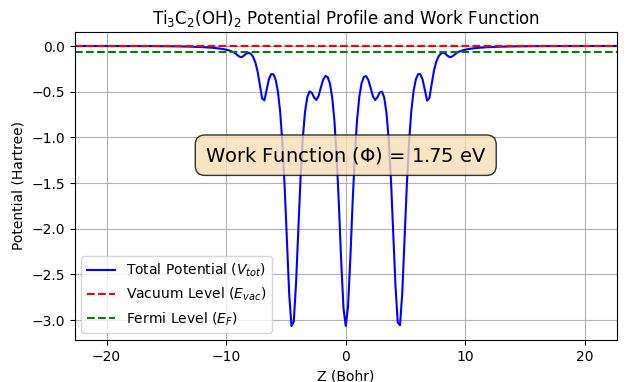
図6. (上から)Ti3C2O2、Ti3C2F2、Ti3C2(OH)2のポテンシャルプロファイルと仕事関数。
計算された仕事関数を表3にまとめ、文献値 [4] と比較します。
表3. 仕事関数 Φ (eV)の比較
| モデル | 本計算値 | 文献値 [4] |
|---|---|---|
| Ti3C2O2 | 5.99 | ~6.14 |
| Ti3C2F2 | 4.88 | ~4.83 |
| Ti3C2(OH)2 | 1.75 | ~1.86 |
考察:
計算結果は、表面官能基の種類が仕事関数に劇的な影響を与えることを明確に示しています。特にTi3C2(OH)2の仕事関数は1.75 eVと極めて低い値となりました。この傾向は文献 [4] の計算結果と非常によく一致しています。文献 [4] によれば、-OH終端MXeneの超低仕事関数は、表面に存在する-OH基が持つ固有の電気双極子モーメントが、材料表面から真空側へ向かう大きな表面双極子を形成し、結果として真空準位を大幅に引き下げるためであると説明されています。逆に、電気陰性度の高い酸素原子で終端されたTi3C2O2は、電子を強く引き付けるため仕事関数が最も大きくなります。フッ素はその中間の値を示しました。この結果は、表面官能基を制御することでMXeneの仕事関数を広範囲にチューニングできる可能性を示唆しています。
まとめ#
本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、代表的なMXeneであるTi3C2の表面を-O, -F, -OHで官能基化した際の構造および電子物性を調査しました。構造最適化によって得られた格子定数は文献値と良い一致を示し、計算の妥当性を確認しました。電子状態計算からは、いずれの官能基化モデルも金属的性質を維持することが示されました。仕事関数の計算では、表面官能基によって値が大きく変化し、特に-OH基で終端した場合に1.75 eVという極めて低い仕事関数が得られることを見出しました。この傾向は文献の報告と一致しており、-OH基の持つ電気双極子モーメントが仕事関数を低下させる主要因であることが示唆されます。本結果は、表面修飾によるMXeneの物性制御の可能性を明確に示しており、将来の電子デバイス応用へ向けた材料設計に有用な知見となります。
本解析の詳細や、研究への適用可能性に関するご相談はこちら
お問い合わせ参考文献#
- M. Naguib, M. Kurtoglu, V. Presser, J. Lu, J. Niu, M. Heon, L. Hultman, Y. Gogotsi, and M. W. Barsoum, "Two-Dimensional Nanocrystals Produced by Exfoliation of Ti3AlC2", Adv. Mater. 37, 4248 (2011).
- T. Hu, J. Wang, H. Zhang, Z. Li, M. Hu, and X. Wang, "Vibrational properties of Ti3C2 and Ti3C2T2 (T= O, F, OH) monosheets by first-principles calculations: a comparative study", Phys. Chem. Chem. Phys. 17, 9997 (2015).
- Y. Xie and P. R. C. Kent, "Hybrid density functional study of structural and electronic properties of functionalized Tin+1Xn (X= C, N) monolayers", Phys. Rev. B 87, 235441 (2013).
- M. Khazaei, M. Arai, T. Sasaki, A. Ranjbar, Y. Liang, and S. Yunoki, "OH-terminated two-dimensional transition metal carbides and nitrides (MXenes) as ultralow work function materials", Phys. Rev. B 92, 075411 (2015).
関連ページ#
- 第一原理計算ソフトウェア Advance/PHASE
- 解析分野:ナノ・バイオ
- 産業分野:材料・化学