Meta-dynamics法によるC4H6電子環状反応の自由エネルギー曲面解析#

PHASE logo

化学反応は、分子がエネルギーの山（活性化障壁）を越えて構造を変化させる現象です。このエネルギー地形を「自由エネルギー曲面」と呼び、その全体像を理解することは、反応のメカニズムを解明し、新しい物質を設計する上で極めて重要です。しかし、通常の分子動力学（MD）シミュレーションでは、系はエネルギーの低い安定な谷に留まりがちで、活性化障壁を越えるような稀な事象を効率的に再現するのは困難です。第一原理計算ソフトウェアAdvance/PHASEでは、このような課題を克服する「Meta-dynamics法」が実装されています。本解析では、この手法を用い、C₄H₆分子の電子環状反応を例として、複雑な反応経路と自由エネルギー曲面の探索を行います。

Keywords: 第一原理計算, Meta-dynamics, 自由エネルギー曲面, 反応経路探索, C4H6, 電子環状反応

計算手法：Meta-dynamics法#

Meta-dynamics法は、化学反応のようなエネルギー障壁が存在する過程を効率的にシミュレーションするための手法です [1, 2]。その基本的な考え方は、シミュレーションの進行とともにエネルギー地形を動的に変化させることにあります。

このプロセスは、エネルギーの谷を「砂」で埋めていく作業に例えることができます（図1）。シミュレーションが特定の構造（エネルギーの谷）を訪れるたびに、その場所に反発的なポテンシャル（バイアスポテンシャル、すなわち「砂」）を少しずつ加えていきます。これにより、一度訪れた場所には再訪しにくくなり、系はまだ探索していない新しい構造へと効率的に押しやられます。

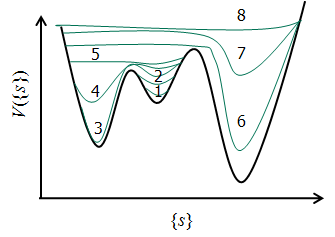
Meta-dynamics法の模式図

図1.　Meta-dynamics法の模式図。シミュレーションはエネルギーの谷(1)から始まり、バイアスポテンシャル(2, 3...)を追加することで徐々に谷を埋め、最終的に系はエネルギー障壁を越えて自由に動けるようになります(8)。

より具体的には、系のポテンシャルエネルギー $U(x)$ に、時間 $t$ と集団変数（Collective Variable, CV） $s$ に依存するバイアスポテンシャル $V_G(s, t)$ を加えます。

$U_{\text{meta}}(x, t) = U(x) + V_G(s(x), t)$

この $V_G(s, t)$ は、一定時間間隔 $\tau$ ごとに、その時点での系の位置 $s(t')$ にガウシアン関数を一つずつ積み重ねていくことで構築されます。

$V_G(s, t) = \sum_{t'=\tau, 2\tau, \dots}^{t} W \exp \left( - \dfrac{\|s - s(t')\|^2}{2\delta s^2} \right)$

ここで、 $W$ はガウシアンの高さ（盛る砂の量）、 $\delta s$ はガウシアンの幅（解像度）を表します。この式は、「系が訪れた場所 $s(t')$ を中心に、小さなポテンシャルの山（ガウシアン）を置いていく」操作そのものです。

この「砂埋め」を十分長い時間続けると、バイアスポテンシャル $V_G(s, t)$ は、元の自由エネルギー曲面 $F(s)$ のくぼみをちょうど埋め尽くすような形になります。その結果、最終的に蓄積されたバイアスポテンシャルは、元の自由エネルギー曲面を反転させたものに近づくため、以下の式で自由エネルギー曲面そのものを得ることができるのです。

$F(s) \approx -V_G(s, t \to \infty) + A$

ここで $A$ は定数です。Meta-dynamicsを用いた計算では、反応を特徴づける幾何学的変数として定義される「集団変数」の選択が非常に重要です。Advance/PHASEには、Meta-dynamics 法に対応したGUIが設けられているため、上記の計算手順をスムーズに実行できます。図2に、Meta-dynamics法を使用する際の設定画面および結果解析のスナップショットを示します。本解析では、C₄H₆の開環・閉環反応を記述するために、特定の原子間距離と二面角を集団変数として設定しました。

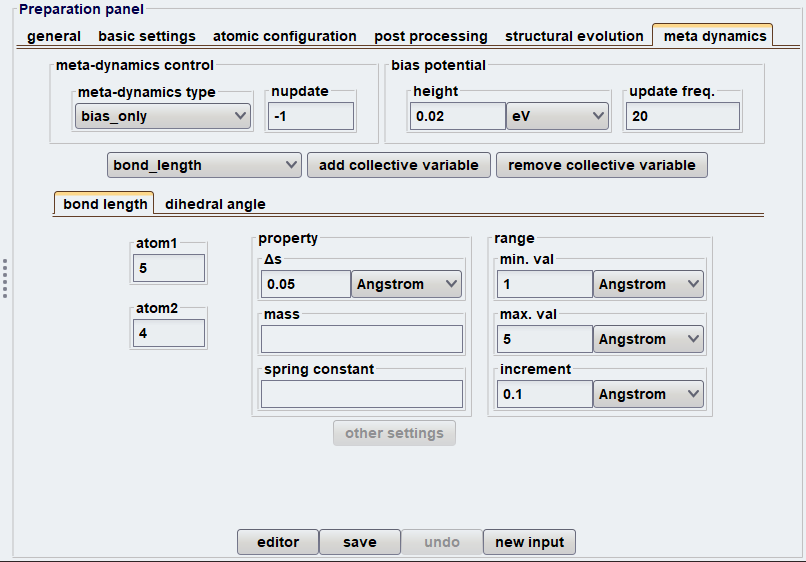
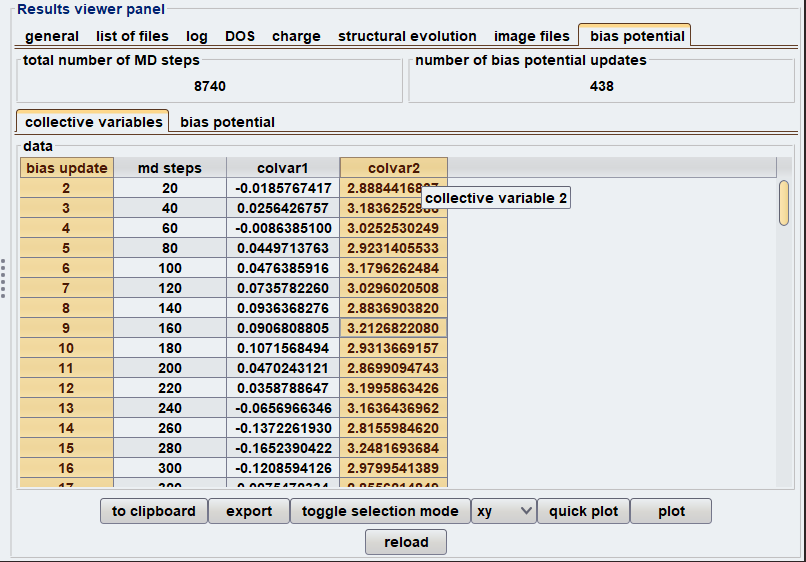
Meta-dynamics法使用時のGUI画面: (a)入力設定

　図2　Meta-dynamics法使用時のGUI画面(上：入力設定、下：結果解析)

計算モデル#

本解析の対象は、C₄H₆分子です。この分子には、図3に示すように、環状構造のシクロブテンと、鎖状構造のcis-1,3-ブタジエン、trans-1,3-ブタジエンという3種類の主要な安定構造（異性体）が存在します。これらの異性体間の変換、特にシクロブテンの開環反応は、炭素-炭素結合の切断と生成を伴うため、高いエネルギー障壁を持つ複雑な反応です。

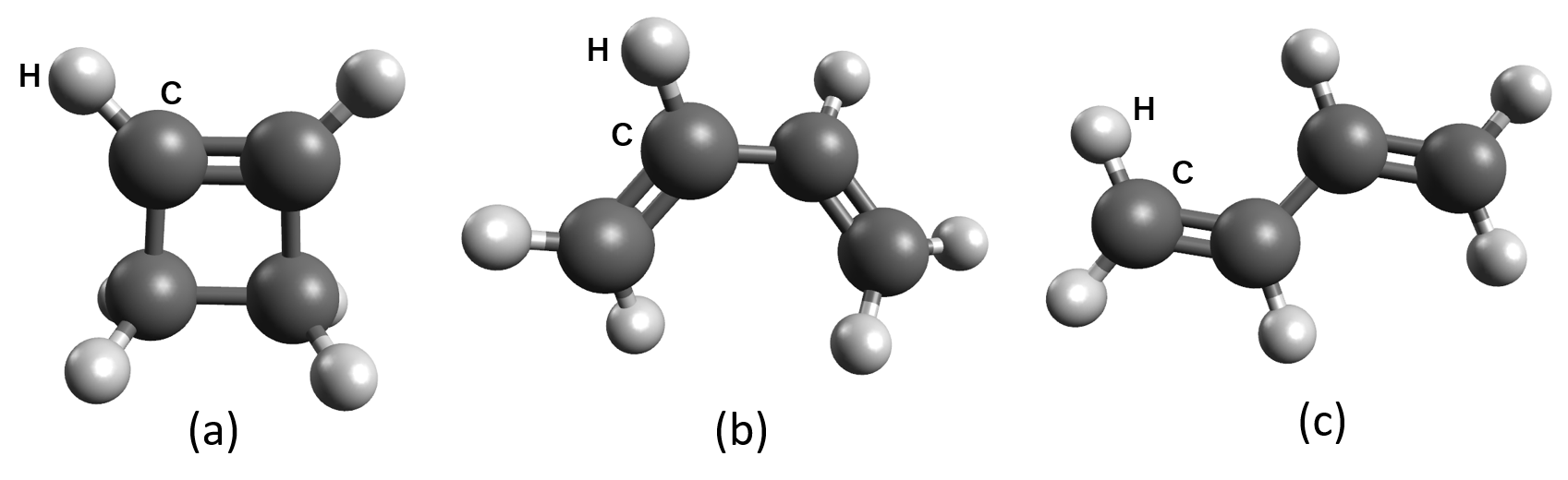
C4H6分子の各構造

図3.　C₄H₆分子の安定構造。 (a)シクロブテン、 (b)cis-1,3-ブタジエン（gauche配座）、(c)trans-1,3-ブタジエン。

シミュレーションは、図4に示すシクロブテンの最適化構造から開始しました。反応経路を探索するための集団変数として、以下の2つを定義しました。

集団変数1： 結合が切断される炭素原子間の距離（図4のC1-C2間）。
集団変数2： 分子骨格のねじれを表す二面角（図4のC1-C4-C3-C2）。

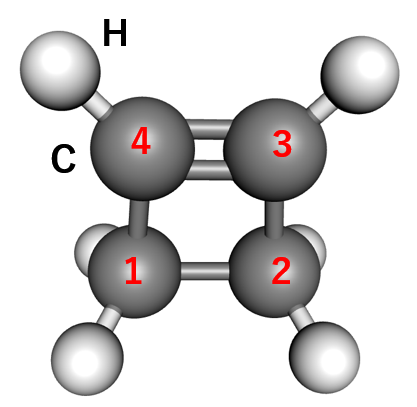
シクロブテンの初期構造

図4.　計算に用いたシクロブテンの初期構造と集団変数の定義に用いたC原子の番号。

計算結果と考察#

自由エネルギー曲面#

図5は、約18,000回のバイアスポテンシャル更新を経て得られたC₄H₆の自由エネルギー曲面です。横軸は二面角、縦軸は炭素間距離に対応し、色の濃淡が自由エネルギーの高さを示しています。

この曲面には、明確に4つのエネルギーの谷（安定点）が現れています。

A (C-C距離 ≈ 1.5 Å, 二面角 ≈ 0) : シクロブテンに対応する初期状態。
B (C-C距離 ≈ 3.3 Å, 二面角 ≈ 0) : cis-1,3-ブタジエン。
C, D (C-C距離 ≈ 3.7 Å, 二面角 ≈ ±3 rad) : 最も安定なtrans-1,3-ブタジエン。

なお、安定点Bは平面的なcis配座に対応していますが、これはより安定な「gauche配座」（ねじれ構造）と、今回の300Kのシミュレーション条件では明確に区別できなかった状態と解釈されます。この結果は、Meta-dynamics法によって、複数の安定構造とそれらを隔てるエネルギー障壁からなる複雑なエネルギー地形が、1回のシミュレーションで見事に描き出されたことを示しています。シクロブテン(A)からブタジエン(B, C, D)への反応は、高いエネルギーの鞍点（図中の黄色い領域）を越える必要があることも一目瞭然です。

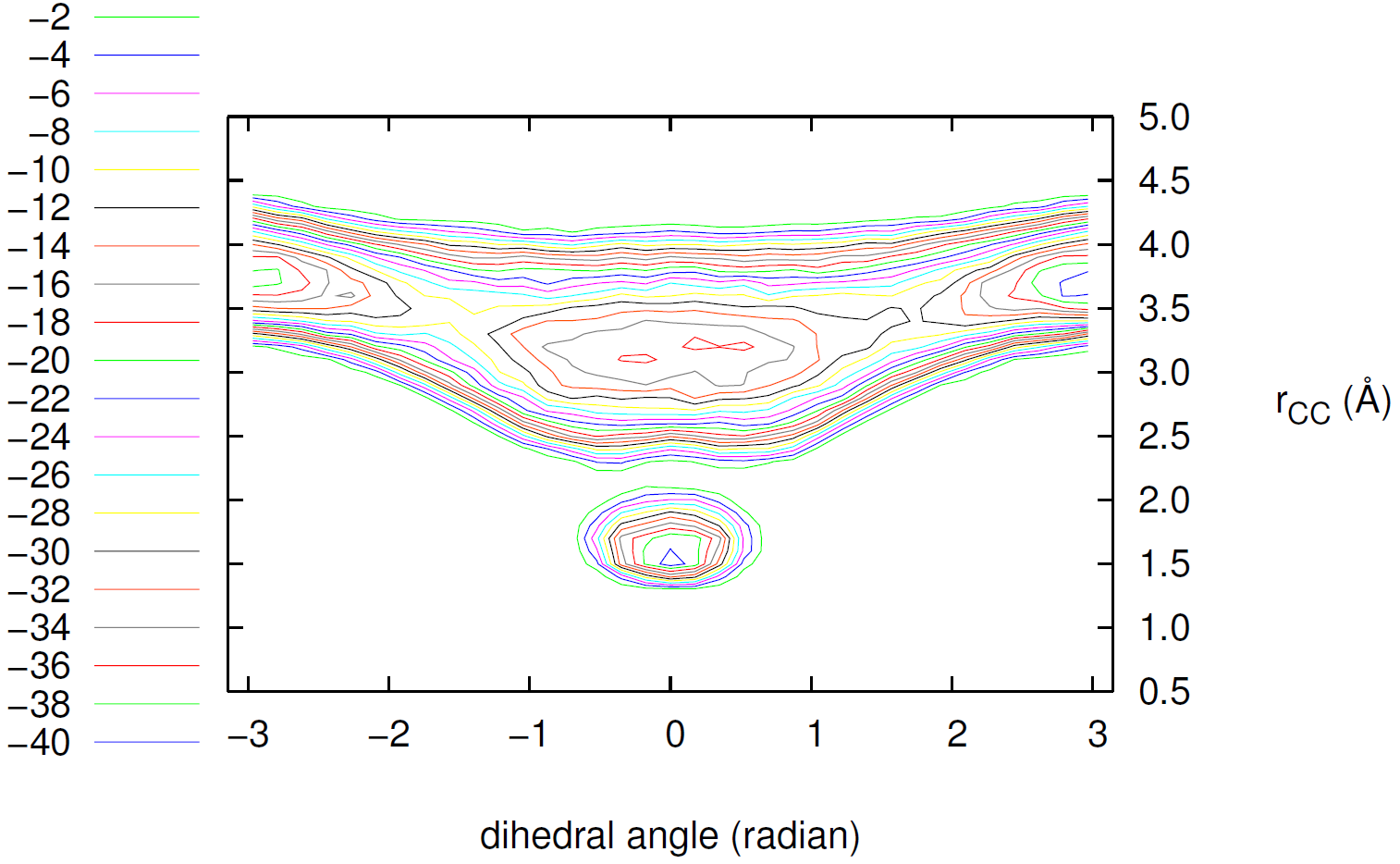
C4H6の自由エネルギー曲面

図5.　Meta-dynamics法で計算されたC₄H₆の自由エネルギー曲面（エネルギー単位: kcal/mol）。A, B, C, Dはエネルギーが極小となる安定構造を示しています。

反応経路の時系列#

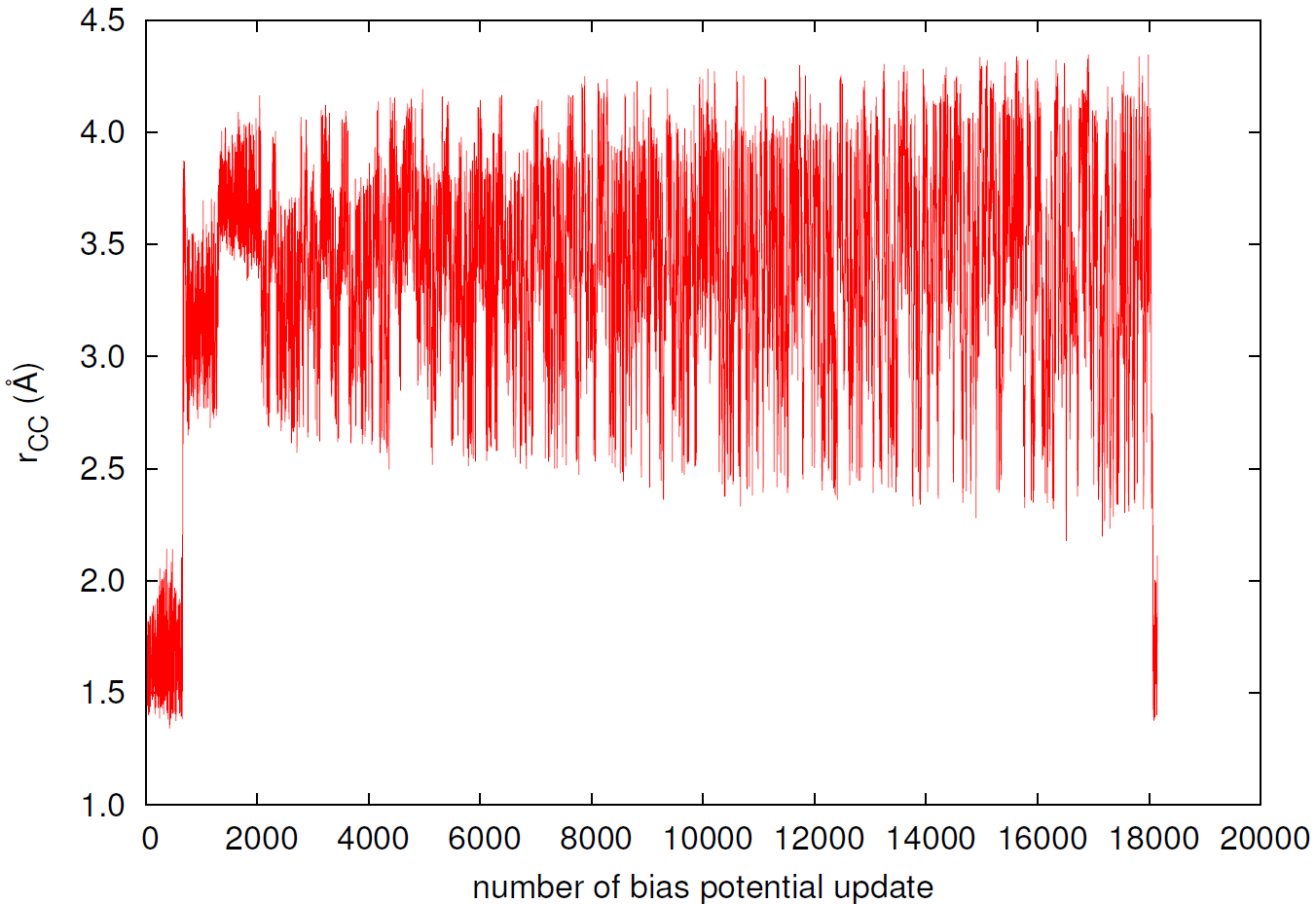
図6と図7は、シミュレーション中に集団変数（炭素間距離と二面角）がどのように時間変化したかを示しています。炭素原子間距離の時間変化

図6.　炭素原子間距離の時系列変化。

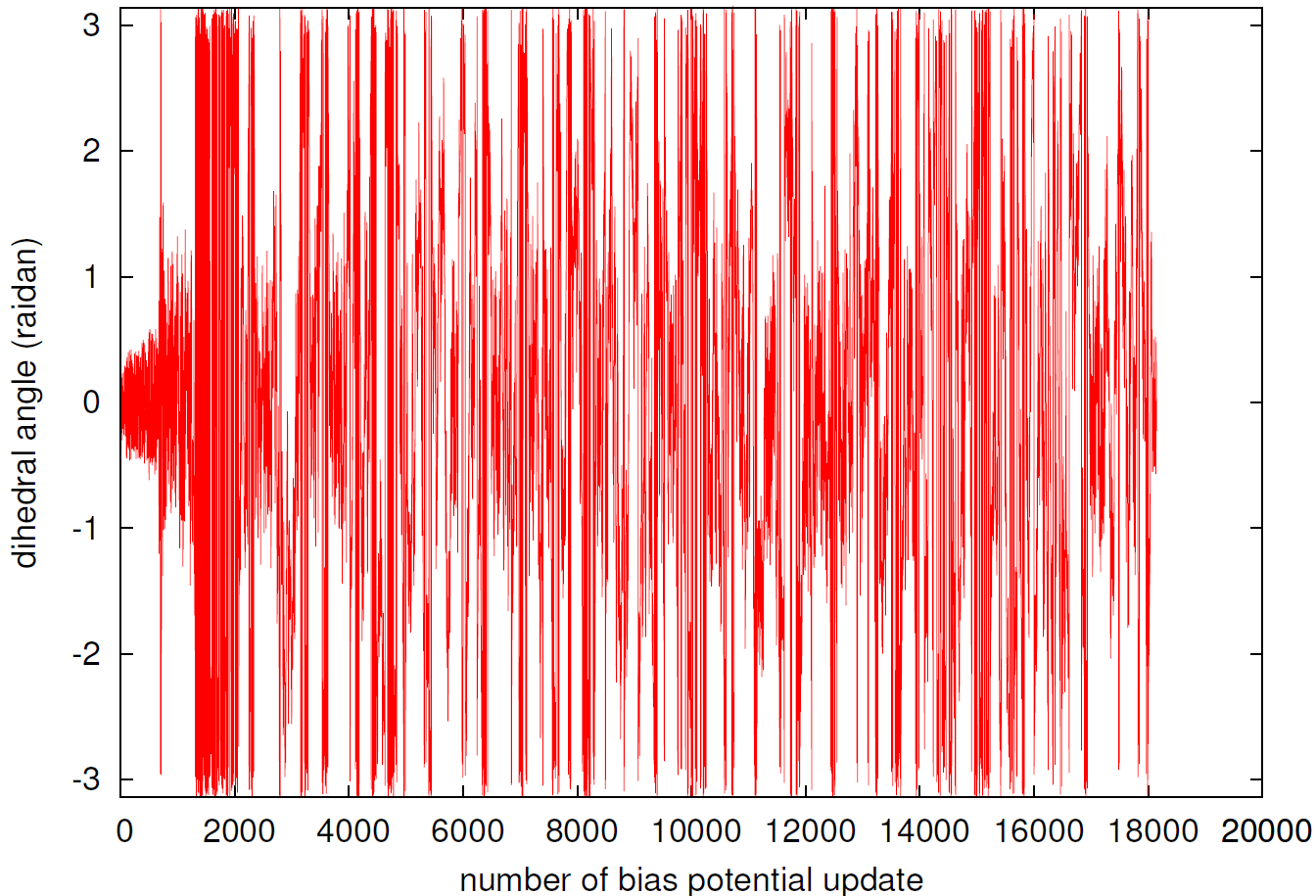
二面角の時間変化

図7.　二面角の時系列変化。

シミュレーション開始後、バイアス更新回数が約700回に達した時点で、炭素間距離が急激に増大し（図6）、系が最初の大きなエネルギー障壁を乗り越えてシクロブテンからブタジエンへと変化したことが分かります。その後、系はブタジエンの広いエネルギーの谷を広範囲に探索し、最終的に約18,000回目の更新で再びシクロブテンの状態へと戻っています。

特に、二面角の時間変化（図7）に注目すると、反応の様子をより詳細に理解できます。開環後、二面角は-πから+πまでの非常に広い範囲を活発に動き回ります。これは、環状で動きが制限されていたシクロブテンとは対照的に、鎖状のブタジエン分子が中心の単結合周りで自由に回転し、cis体やtrans体など多様な構造を取りうることを示しています。この幅広い探索により、ブタジエンが取りうる様々な配座（コンフォメーション）が網羅的にサンプリングされており、約18,000回目の更新で再び二面角が0付近のシクロブテン構造に戻ることで、反応サイクルが一巡したことが確認できます。

図8は、シミュレーション中に見られた分子構造のスナップショットです。初期の環状構造(a)から、遷移状態に近い構造(b)を経て、多様な鎖状構造(c)が実現され、最終的に元の環状構造(d)に回帰している様子が分かります。

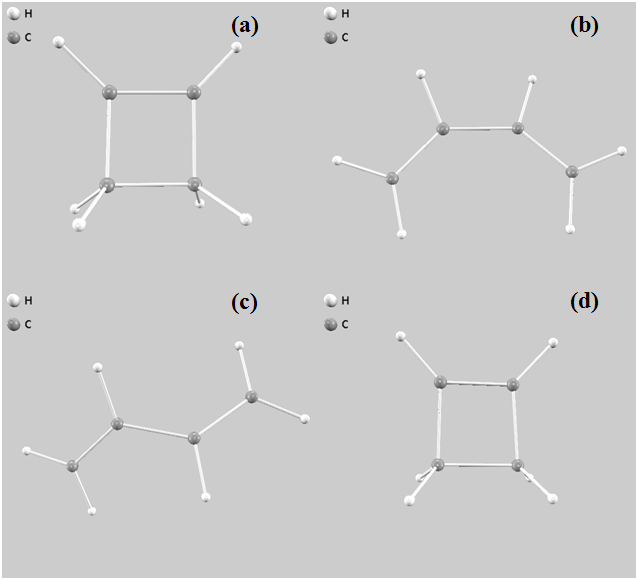
Meta-dynamicsシミュレーション中のスナップショット

図8. シミュレーション中の分子構造スナップショット。(a)バイアスポテンシャル2回更新 (b)バイアスポテンシャル690回更新 (c)バイアスポテンシャル1,500回更新 (d) バイアスポテンシャル18,070回更新。

まとめ#

本解析では、第一原理計算ソフトウェアAdvance/PHASEに実装されていたMeta-dynamics手法を用いて、C₄H₆分子の電子環状反応における自由エネルギー曲面を明らかにしました。この手法により、通常のシミュレーションでは到達困難なエネルギー障壁を乗り越え、反応物、生成物、そしてそれらの間の遷移経路を含む広範な構造空間を効率的に探索することができました。計算により得られたポテンシャルエネルギー曲面において、既知の安定異性体に対応する複数のエネルギーの谷が再現され、反応メカニズムの解明に重要な情報となります。

参考文献#

A. Laio and M. Parrinello, "Escaping free-energy minima", Proceedings of the National Academy of Sciences 99, 12562 (2002).
A. Laio and F. L. Gervasio, "Metadynamics: a method to simulate rare events and reconstruct the free energy in biophysics, chemistry and material science", Reports on Progress in Physics 71, 126601 (2008).