DFTによるMoS2ナノチューブの構造・電子状態の第一原理解析#

二硫化モリブデン(MoS2)ナノチューブは、そのユニークな半導体特性から、ナノエレクトロニクスや触媒分野での応用が期待されています。特にナノチューブの直径やカイラリティ(巻き方)によって電子状態が大きく変化することが知られています。本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、密度汎関数理論(DFT)に基づいてArmchair型 (6, 6) MoS2ナノチューブの構造最適化を行い、その電子的特性(状態密度、バンド構造、電荷密度)を詳細に解析しました。
Keywords: 第一原理計算, DFTシミュレーション, MoS2ナノチューブ, Armchair (6, 6), 構造最適化, 電子状態, バンドギャップ, 状態密度, 電荷密度
計算モデルと計算条件#
計算モデルとして、Armchair型のMoS2 (6, 6) ナノチューブを採用しました。チューブ軸方向(Z軸)に周期境界条件を適用するため、ユニットセル(単位胞)モデルを使用します。ナノチューブ間の相互作用を排除するため、XY方向には約18Åの十分な真空層を設けました。図1に、最適化されたMoS2 (6, 6) ナノチューブの構造を示します。
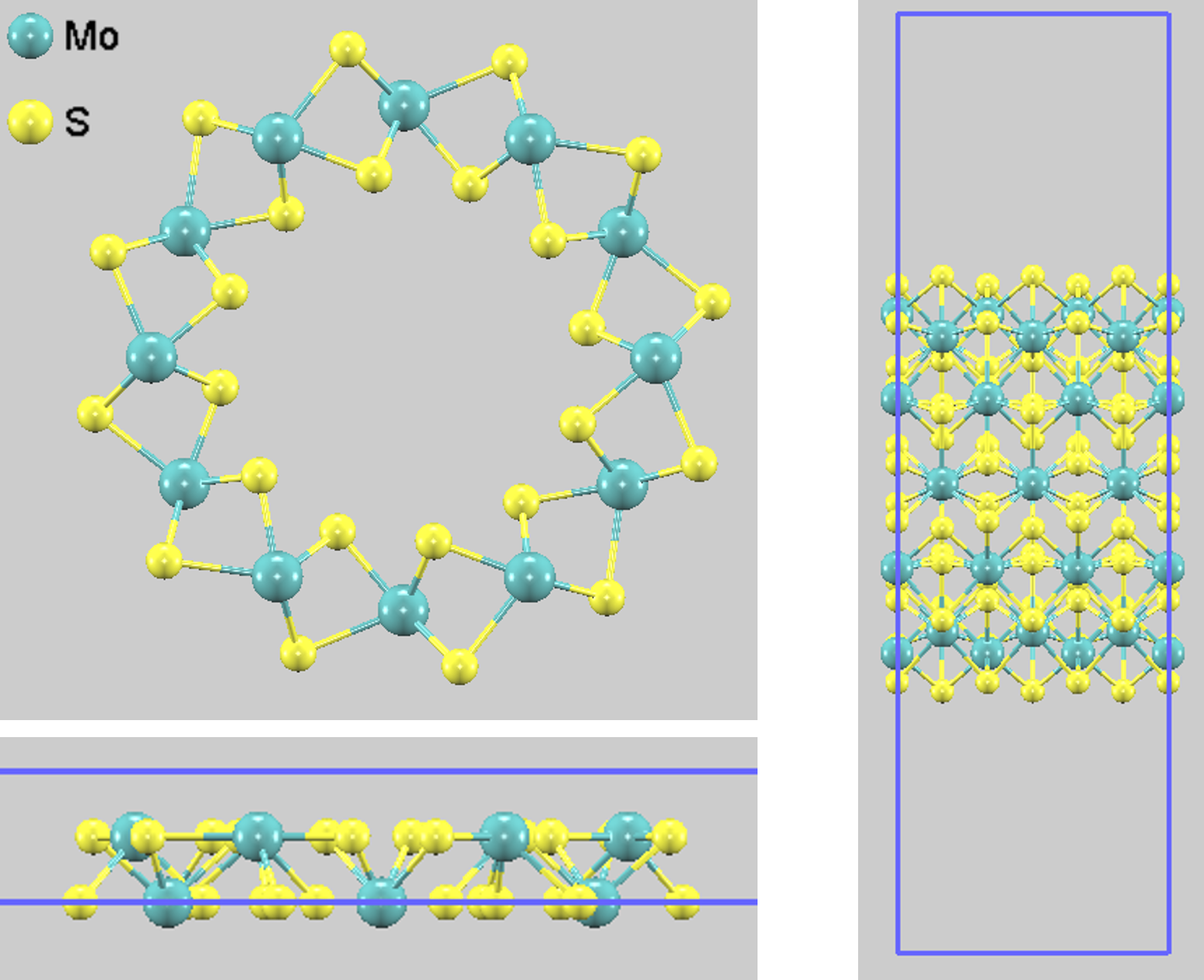
図1. Armchair MoS2 (6, 6) ナノチューブの最適化構造。左上: ユニットセルの正面図、左下: ユニットセルの上面図、右: 側面図(視認性のため、1x1x3スーパーセルで表示)。Mo原子を水色、S原子を黄色で示しています。
本解析で用いた主な計算条件は表1に示されています。
表1. 計算条件の概要
| 項目 | 設定 |
|---|---|
| 擬ポテンシャル | ウルトラソフト擬ポテンシャル |
| 交換相関汎関数 | GGA (PBE) |
| 波動関数のカットオフエネルギー | 25 Rydberg (約340 eV) |
| k点サンプリング (SCF) | 1x1x6 |
計算結果と考察#
構造最適化#
Advance/PHASEを用いてナノチューブの構造最適化計算を行いました。最適化されたArmchair (6, 6) ナノチューブの内径は 8.786 Å、外径は 14.841 Å となりました。
この結果は、文献 [1] で報告されている計算値(内径:8.7 Å、外径:14.784 Å)、および文献 [2] の計算値(内径:8.9 Å) と良好な一致を示しており、本計算の妥当性を裏付けています。
電子状態 (状態密度とバンド図)#
次に、最適化された構造を用いて電子状態を解析しました。図2に状態密度(DOS)を示します。フェルミエネルギー(、0 eV)近傍に状態が存在せず、明確なバンドギャップが形成されていることが確認できます。
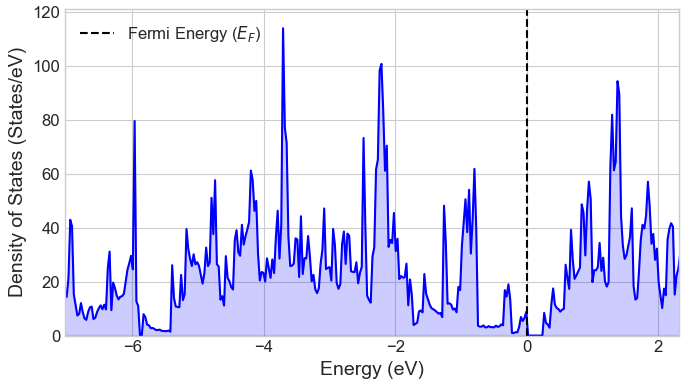
図2. MoS2 (6, 6) ナノチューブの状態密度(DOS)。フェルミエネルギー(、黒破線)は 0 eV に設定されています。
図3にバンド図を示します。バンド図は、チューブ軸方向(点からZ点)についてプロットしています。この結果から、価電子帯の頂上(VBM)は点付近に、伝導帯の底(CBM)は点とZ点の中間付近に位置しており、このナノチューブが間接遷移型の半導体であることがわかります。
バンドギャップの大きさは 約 0.238 eV と計算されました。この値は、文献 [3] で報告されている理論値(間接ギャップ:約 0.22 eV)ともよく一致しています。
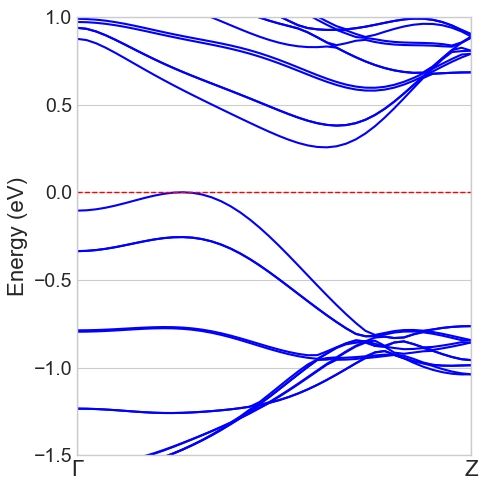
図3. MoS2 (6, 6) ナノチューブのバンド図。フェルミエネルギーを 0 eV(赤破線)としています。間接遷移型のバンド構造が確認できます。
電荷密度#
電子状態の理解を深めるため、電荷密度分布を可視化しました。図4に全電荷密度を示します。電荷(オレンジ色の等値面)は、主にS原子(黄)の周囲、およびMo原子(水色)とS原子の結合領域に局在しており、MoS2のS-Mo-Sの3層構造と共有結合的な性質を反映しています。
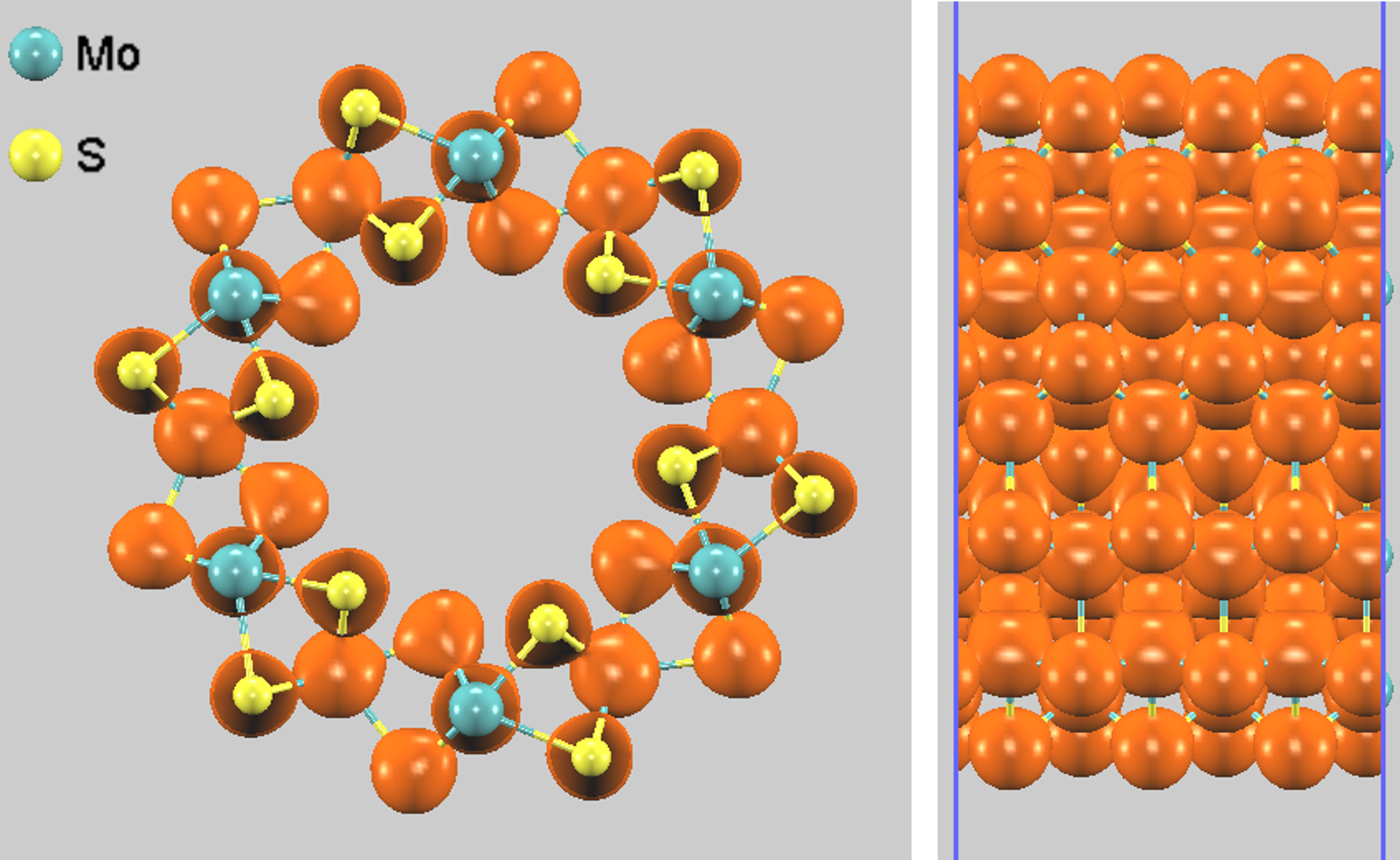
図4. MoS2 (6, 6) ナノチューブの全電荷密度の分布。
さらに、バンドギャップを挟んだ電子軌道の寄与を調べるため、VBM付近とCBM付近の部分電荷密度を解析しました(図5、図6)。
- VBM付近(図5): 主にMo原子の d 軌道と、S原子の p 軌道の混成によって形成されていることがわかります。
- CBM付近(図6): 主にMo原子の d 軌道によって構成されています。
これらのバンドギャップ近傍の電子状態(フロンティア軌道)は、主にMo原子のd軌道によって支配されています 。これらの軌道のエネルギー準位や空間的な広がり、対称性は、物質が光を吸収・放出する際の効率(光学的特性)や、電子や正孔が物質中をどの程度動きやすいか(電気伝導性、キャリア移動度)に直接関わってきます。 例えば、直接遷移型の半導体は発光デバイス(LEDなど)に適している一方、キャリア移動度はトランジスタなどの電子デバイスの性能を左右します。今回計算したArmchair (6, 6) ナノチューブは間接遷移型であり、この点はバルクのMoS2と類似しています。
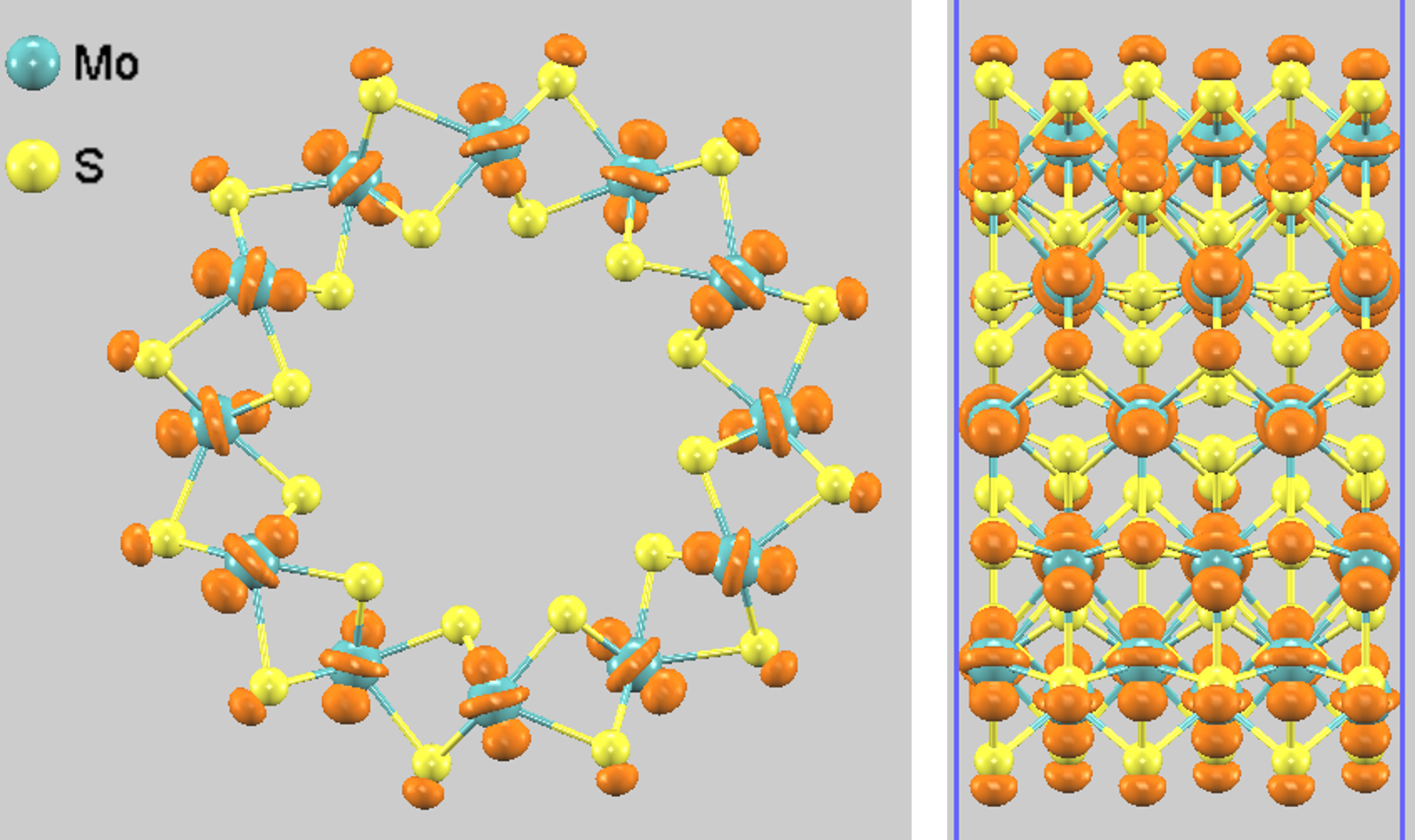
図5. MoS2 (6, 6) ナノチューブのVBM近傍の部分電荷密度の分布。
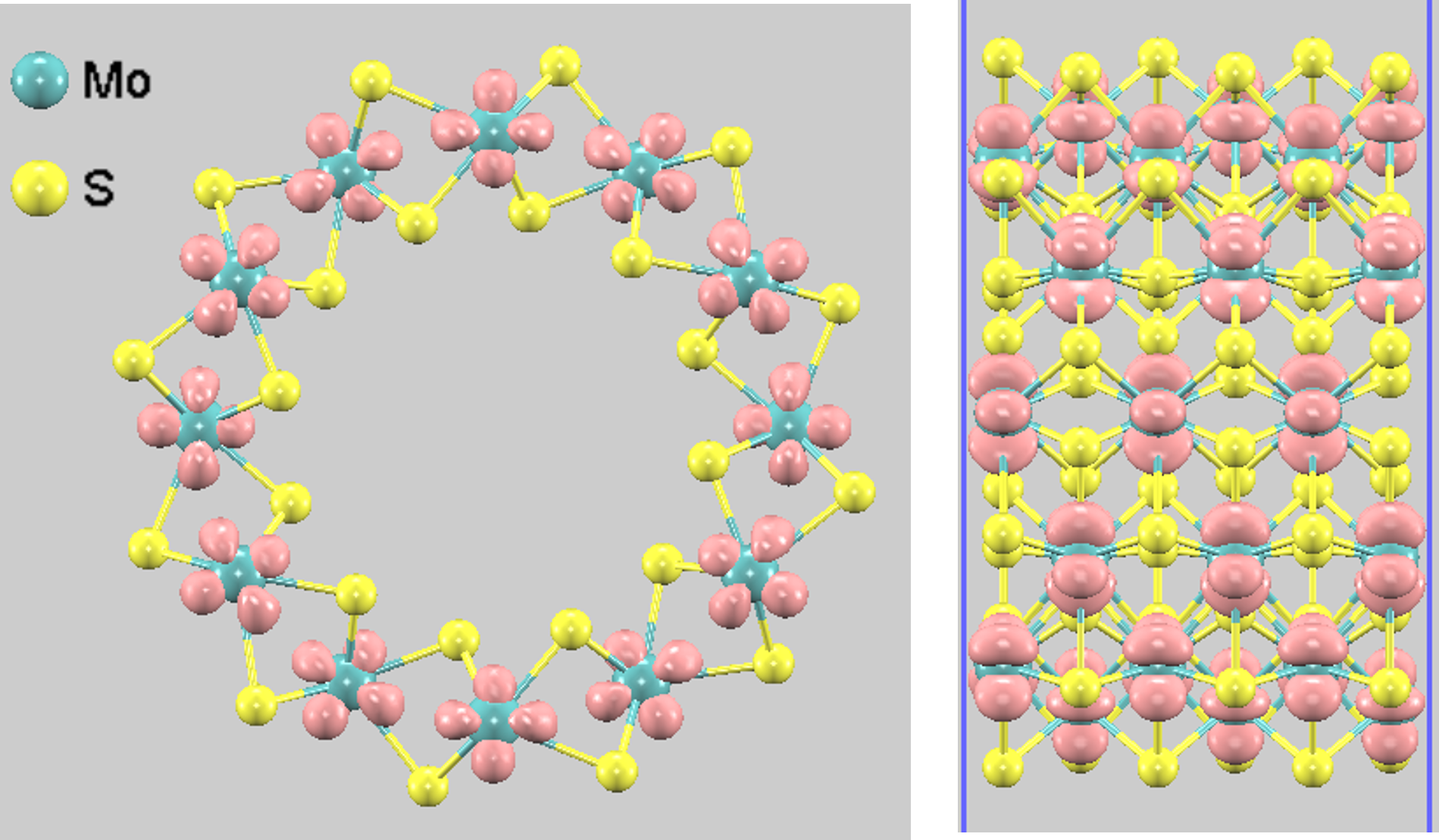
図6. MoS2 (6, 6) ナノチューブのCBM近傍の部分電荷密度の分布。
まとめ#
本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、Armchair型 (6, 6) MoS2ナノチューブの構造物性と電子状態を詳細に解析しました。構造最適化によって得られたナノチューブの直径は、過去の文献値とよく一致しました。電子状態解析の結果、(6, 6) MoS2ナノチューブは約 0.238 eV の間接バンドギャップを持つ半導体であることが示され、文献値と整合しています。さらに、電荷密度解析により、バンドギャップ近傍の電子状態が主にMo原子の d 軌道によって支配されていることが明らかになりました。DFTによる第一原理計算は、ナノ材料の複雑な構造と電子物性の関係性を高精度に解明できることが示されました。
本解析の詳細や、研究への適用可能性に関するご相談はこちら
お問い合わせ参考文献#
- R. Ansari, S. Malakpour, M. Faghihnasiri, and S. Sahmani, "An ab initio investigation into the elastic, structural and electronic properties of MoS2 nanotubes", Superlattices and Microstructures 82, 188 (2015).
- G. Seifert, H. Terrones, M. Terrones, G. Jungnickel, and T. Frauenheim, "Structure and electronic properties of MoS2 nanotubes", Physical Review Letters 85, 146 (2000).
- J. Xiao, M. Long, X. Li, H. Xu, H. Huang, and Y. Gao, "Theoretical prediction of electronic structure and carrier mobility in single-walled MoS2 nanotubes", Scientific Reports 4, 4327 (2014).
関連ページ#
- 第一原理計算ソフトウェア Advance/PHASE
- 解析分野:ナノ・バイオ
- 産業分野:材料・化学