MoS₂ナノリボンの第一原理計算: エッジ特性#

PHASE logo

MoS₂（二硫化モリブデン）は、グラフェンのような二次元層状物質であり、次世代のナノデバイス材料として注目されています。MoS₂をナノスケールのリボン状に加工した「ナノリボン」は、その端（エッジ）の原子配列によって特異な物性を示すことが期待されます。特に、リボンの端の形状が「ジグザグ(zigzag)」型か「アームチェア(armchair)」型かによって、電子的・磁気的特性が大きく変化することが理論的に予測されています。本解析では、第一原理計算ソフトウェアAdvance/PHASE を用い、ジグザグ型とアームチェア型のMoS₂ナノリボンの構造を最適化し、その磁性、バンド構造、状態密度を計算することで、エッジ形状が物性に与える影響を詳細に調査します。

Keywords: 第一原理計算, MoS₂, ナノリボン, エッジ特性, ジグザグ, アームチェア, 磁性, 電子状態

計算モデルと計算条件#

本解析では、代表的な2種類のエッジ構造を持つMoS₂ナノリボンモデルを構築しました。

1つ目は、ジグザグ(zigzag)エッジを持つナノリボン（5-ZNR）です。モデルの幅(Nz)は、リボン幅を横切るジグザグの線の数（このモデルでは5）で定義されます。図1に最適化後の構造（上面図、斜視図、および視認性を高めたスーパーセル）を示します。

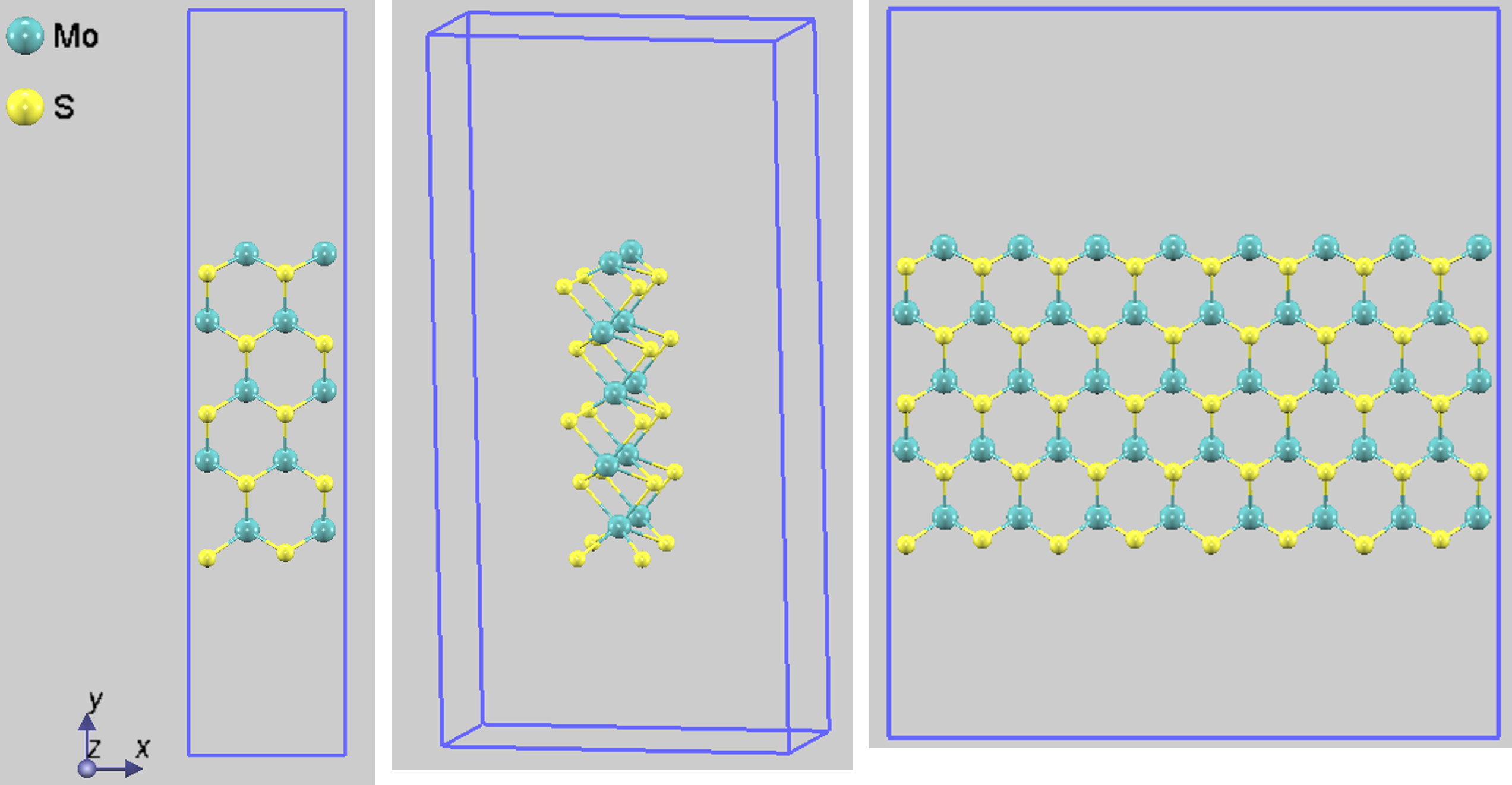
5-ZNRの最適化構造

図1.　ジグザグ(zigzag)エッジを持つ 5-ZNR の最適化構造。 (左) 単位胞の上面図、(中央) 斜視図、(右) 視認性向上のための4x1x1スーパーセル。

2つ目は、アームチェア(armchair)エッジを持つナノリボン（8-ANR）です。モデルの幅(Na)は、リボン幅を横切るダイマー線の数（このモデルでは8）で定義されます。図2に最適化後の構造を示します。

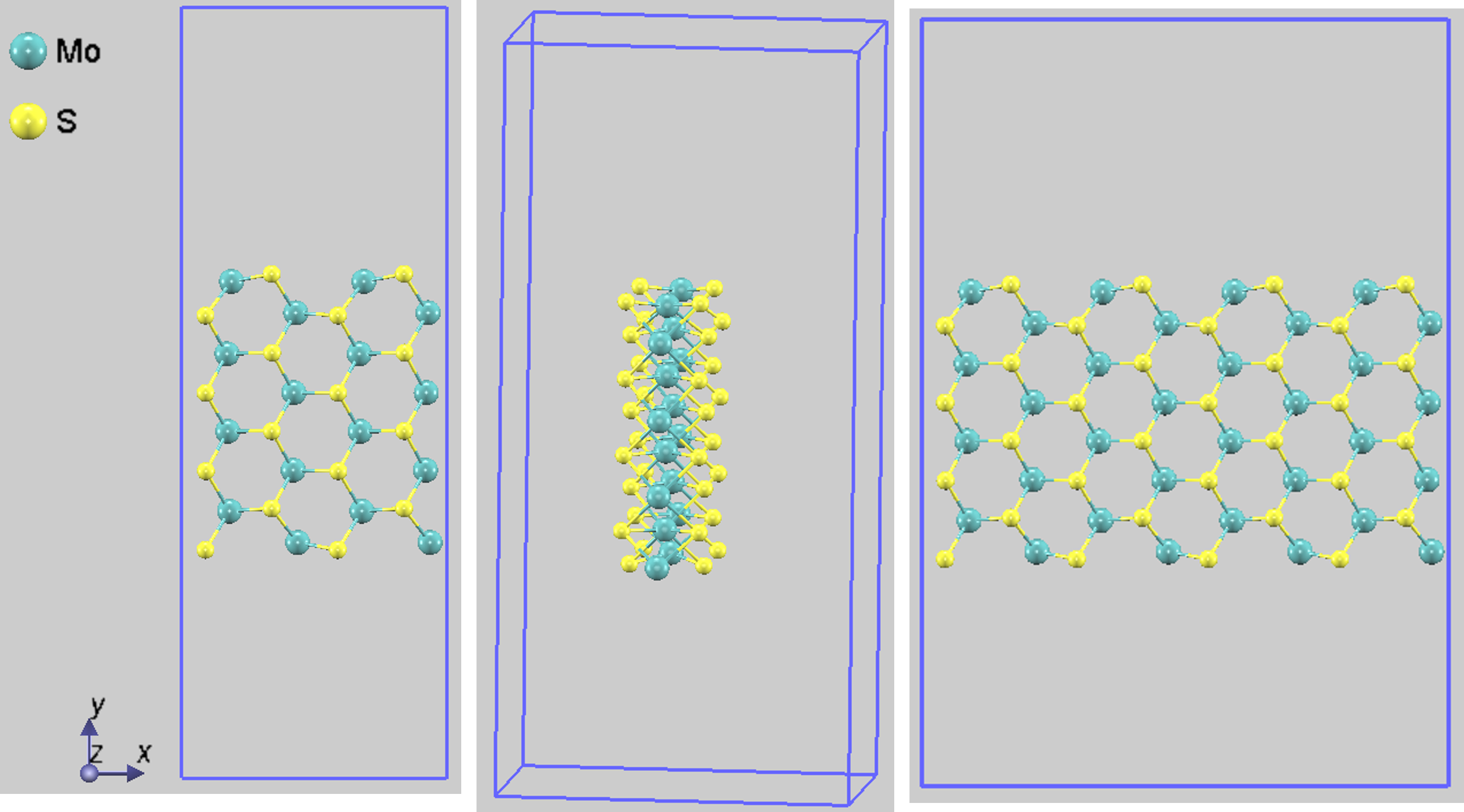
8-ANRの最適化構造

図2.　アームチェア(armchair)エッジを持つ 8-ANR の最適化構造。 (左) 単位胞の上面図、(中央) 斜視図、(右) 視認性向上のための2x1x1スーパーセル。

本解析で用いた主な計算条件は表1に示されています。

表1.　主な計算条件

項目	設定
擬ポテンシャル	ウルトラソフト擬ポテンシャル
交換相関汎関数	GGA-PBE
波動関数のカットオフエネルギー	25 Rydberg
k点サンプリング (SCF)	5-ZNR: 5x1x1, 8-ANR: 3x1x1

計算結果と考察#

磁性の比較#

まず、5-ZNRモデルの磁性を解析しました。スピン分極を考慮した計算の結果、5-ZNRは強磁性 (Ferromagnetic) の基底状態を持つことが示されました。図3にスピン密度分布を示します。スピン密度（青色と赤色の領域）はリボンの内部にはほとんど存在せず、両端のエッジ部分に局在していることが明確に観測されます。これは、エッジの特異な原子・電子構造（ダングリングボンドなど）が磁性の起源であることを強く示唆しています。

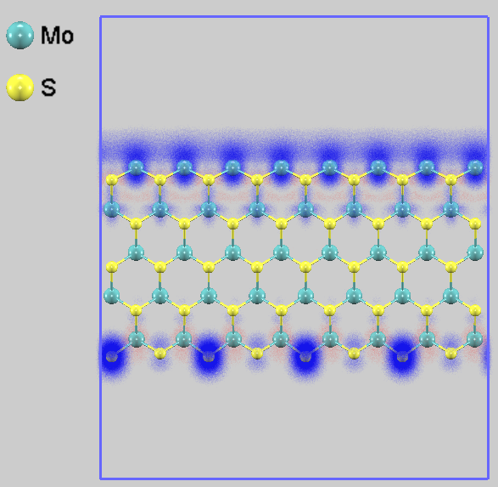
5-ZNR スピン密度分布

図3.　5-ZNRのスピン密度分布。エッジ原子（特にMoとS）にスピンが局在している様子がわかります。

一方、8-ANRモデルでは磁気モーメントは発生せず、非磁性 (Non-magnetic) の基底状態であることが確認されました。この結果は文献 [1] と整合しており、エッジ構造がジグザグ型かアームチェア型かによって、ナノリボンの磁気的特性が質的に異なることを示しています。

バンド構造と状態密度 (5-ZNR)#

次に、5-ZNRの電子状態を解析しました。図4にスピン別のバンド構造を示します。実線（Spin Up）と破線（Spin Down）のバンドが非対称となっており、強磁性体であることを裏付けています。さらに重要な点として、複数のバンドがフェルミエネルギー（E_F = 0 eV）を横切っており、この材料が金属的 (Metallic) であることが示されました。

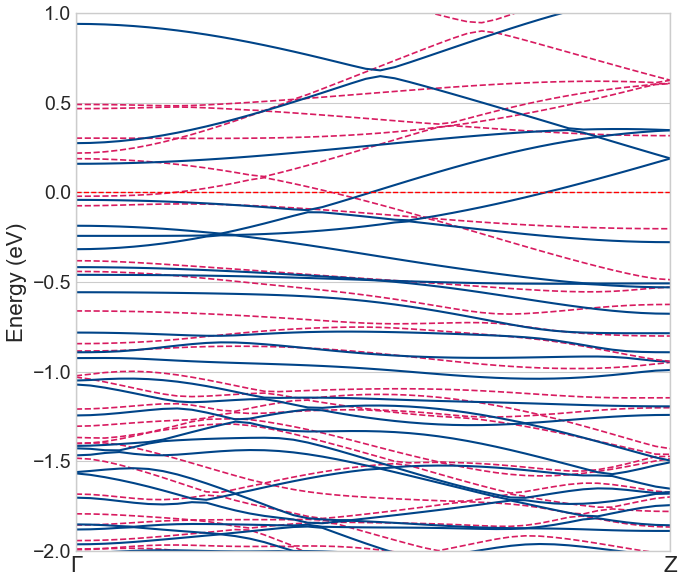
5-ZNR バンド構造

図4.　5-ZNRのバンド構造。実線(Spin Up)と破線(Spin Down)がフェルミ準位(0 eV)を横切っており、強磁性金属であることを示します。

図5の状態密度(DOS)からも、この傾向は明らかです。フェルミエネルギー（黒破線）において、Spin Up（青色）、Spin Down（ピンク色）共に有限の状態密度が存在しており、金属であることが確認できます。スピンアップとスピンダウンのDOSが非対称であることも、磁性を持つことと一致しています。

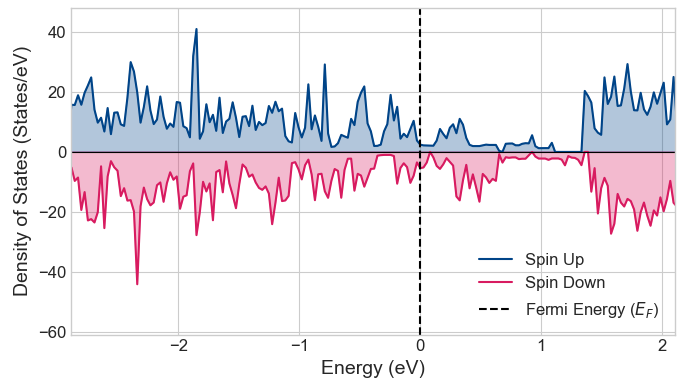
5-ZNR 状態密度

図5.　5-ZNRの状態密度(DOS)。フェルミ準位(0 eV)で有限のDOSを持ち、金属であることを示す。

バンド構造と状態密度 (8-ANR)#

対照的に、8-ANRモデルの電子状態は全く異なります。図6のバンド構造では、フェルミエネルギー（赤破線, 0 eV）近傍にバンドが存在せず、価電子帯と伝導帯の間に明確なバンドギャップが形成されています。

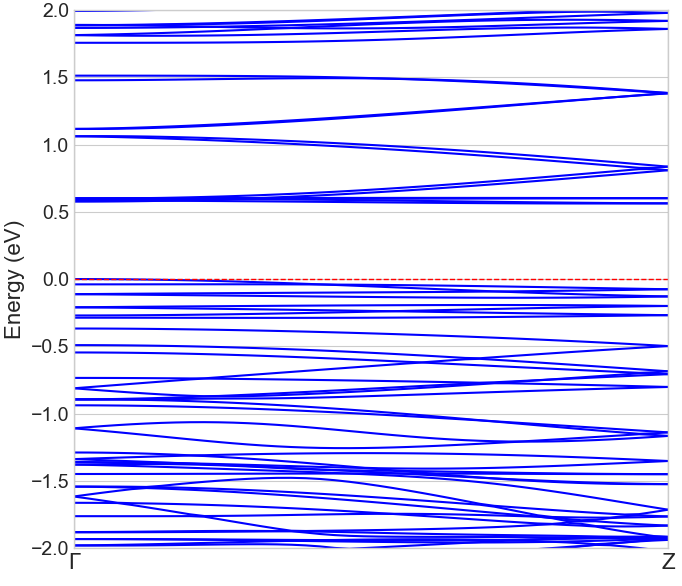
8-ANR バンド構造

図6.　8-ANRのバンド構造。フェルミ準位(0 eV)近傍にバンドギャップが形成されている。

図7の状態密度(DOS)からも、フェルミエネルギー（黒破線）近傍で状態密度がゼロになっており、8-ANRが半導体 (Semiconducting) であることが確認できます。

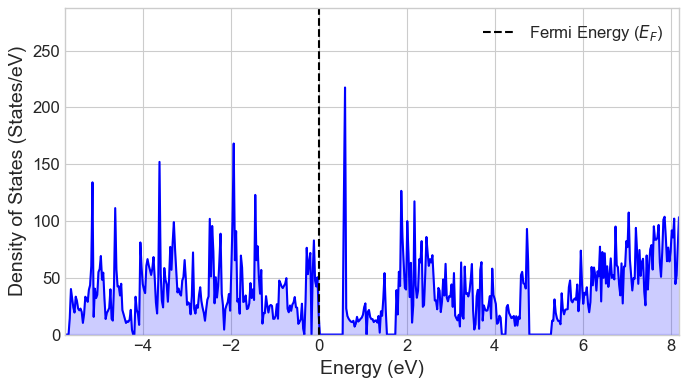
8-ANR 状態密度

図7.　8-ANRの状態密度(DOS)。フェルミ準位(0 eV)にバンドギャップを持つ半導体特性を示します。

HOMO電荷密度と文献値との比較#

8-ANRの半導体特性、特にバンドギャップの端（バンドエッジ）がどの原子に由来するかを調査するため、HOMO（最高被占軌道）近傍の部分電荷密度をプロットしました（図8）。この電荷密度（左図の青色領域、右図のオレンジ色の領域）は、リボンの内部ではなく、エッジ部分に局在していることが分かります。これは、バンドギャップの大きさがエッジ原子の状態によって強く影響されることを示唆しています。

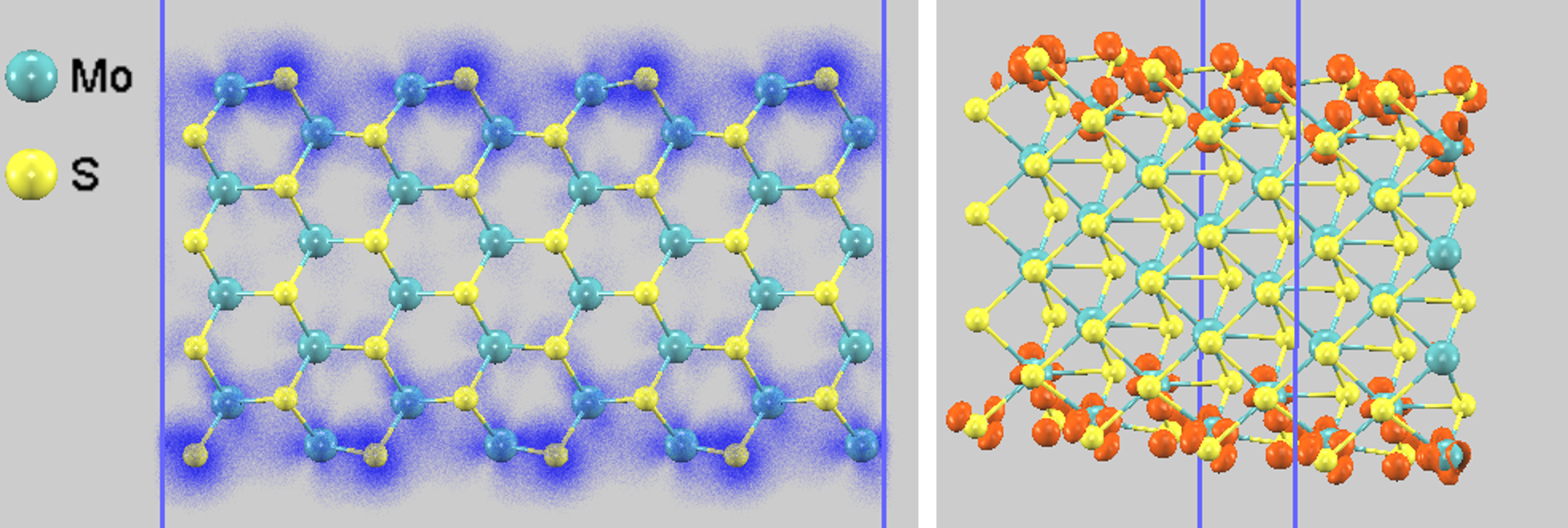
HOMO側部分電荷密度

図8.　8-ANRのHOMO側の部分電荷密度。左：cloud分布、右：等値面。

本計算で得られた8-ANRのバンドギャップは 0.541 eV でした。これは、文献 [1] の計算値 0.55 eV と良好な一致を示しており、本計算手法の妥当性を裏付けています。さらに、文献 [2] でも、アームチェア型ナノリボンのバンドギャップに関する同様の結果が報告されており、そのキャリア移動度についても詳細な計算が行われています。

まとめ#

本解析では、第一原理計算ソフトウェアAdvance/PHASEを使用し、MoS₂ナノリボンのエッジ特性を調査しました。計算の結果、5-ZNR（ジグザグ）モデルは強磁性の金属である一方、8-ANR（アームチェア）モデルは磁性を持たないバンドギャップ 0.541 eV の半導体となることが分かりました。このように、MoS₂ナノリボンはそのエッジ形状（ジグザグまたはアームチェア）を変えるだけで、金属/半導体特性および磁性/非磁性特性を劇的に制御できることが第一原理計算によって確認されました。この特性は、将来のスピントロニクスデバイスやナノ電子デバイスへの応用において重要な知見となります。

参考文献#

Y. Li, Z. Zhou, S. Zhang, and Z. Chen, "MoS₂ nanoribbons: high stability and unusual electronic and magnetic properties", J. Am. Chem. Soc. 130, 16739 (2008).
Y. Cai, G. Zhang, and Y. W. Zhang, "Polarity-reversed robust carrier mobility in monolayer MoS₂ nanoribbons", J. Am. Chem. Soc. 136, 6269 (2014).

MoS2ナノリボンの第一原理計算: エッジ特性#