金属水素化物MgH₂不安定化の第一原理計算: 添加剤による水素放出促進効果#

PHASE logo

金属水素化物（代表例：MgH₂）は、高密度に水素を貯蔵できる材料として期待されていますが、非常に安定であるという課題があります。MgH₂から水素（H₂）を取り出すためには250℃以上といった高温が必要であり、実用化の大きな障壁となっています。そこで、より低い温度でH₂を放出させるための「不安定化（Destabilization）」技術が求められています。本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、添加剤（Si）がMgH₂の水素放出エンタルピー（ΔH）をどれだけ低減できるか（不安定化できるか）を定量的に評価します。

Keywords: 第一原理計算 (DFT), 水素貯蔵材料, 金属水素化物, MgH₂, 不安定化, 添加剤, 反応エンタルピー

計算方法#

添加剤（Si）の効果を明確にするため、「添加剤なし」の基準反応と「Si添加」の不安定化反応の2つのエンタルピー（ΔH）を直接比較します。

A. 基準反応（添加剤なし）#

$\text{MgH}_2 \rightarrow \text{Mg} + \text{H}_2$ MgH₂が分解し、金属Mgと水素H₂になる基本的な反応です。この反応エンタルピーΔH_Aが、材料の実用性を判断する基準となります。

B. 不安定化反応（Si 添加）#

$2\text{MgH}_2 + \text{Si} \rightarrow \text{Mg}_2\text{Si} + 2\text{H}_2$ あらかじめMgH₂と添加剤Siを混合しておく系を想定します。H₂放出後、残ったMgがSiと即座に反応し、非常に安定な化合物である Mg₂Si を形成します。この「安定な受け皿」が形成されることにより、系全体としてH₂を放出しやすくなる（＝不安定化する）と考えられます。

エンタルピー（ΔH）の算出#

各反応のエンタルピー（ΔH）は、各物質の全エネルギー(E)から以下のように算出します。 $\Delta H_A = E(\text{Mg}) + E(\text{H}_2) - E(\text{MgH}_2) \\ \Delta H_B = E(\text{Mg}_2\text{Si}) + 2 * E(\text{H}_2) - (2 * E(\text{MgH}_2) + E(\text{Si}))$

注記：ZPE（ゼロ点エネルギー）補正の省略について

本解析では、2つの反応（AとB）の「差」を比較することが目的であるため、ZPE補正を省略しています。これは、以下の理由に基づいています。

反応エンタルピーのZPE補正（ΔZPE）は、「生成物のZPE合計」から「反応物のZPE合計」を引いた値であり、その寄与は主に軽い原子（H）の振動に由来します。
両反応（A, B）とも、「固体中のH（in MgH₂）」が「気体中のH（in H₂）」に変わる点が、ΔZPEの最大の寄与項となります。H₂ 1モルあたりで比較すると、これは両反応の共通項です。
したがって、H₂ 1モルあたりのZPE補正の差（ $\Delta \text{ZPE}_A$ と $\Delta \text{ZPE}_B/2$ の差）は、残りの重い原子のみで構成される固体（Mg, Si, Mg₂Si）のZPEの差に起因します。
これらの重い原子が関わるZPEの差は、Hが関わる上記の大きな共通項に比べて十分に小さいため、無視できるとみなせます。
その結果（共通項はほぼ等しく、差分の要因は無視できるため）、 $\Delta \text{ZPE}_A \approx \Delta \text{ZPE}_B/2$ と近似することができます。

したがって、不安定化の効果（ $\Delta H_A - \Delta H_B/2$ ）は、ZPE補正を行わない0Kの全エネルギー比較で十分に議論可能であると判断しました。

計算モデルと計算条件#

DFT計算にはMgH₂（正方晶構造、P4₂/mnm対称性）、Mg₂Si（立方晶構造、Fm3m対称性）、Si（diamond構造）、Mg（六方晶HCP構造）の各結晶モデル、およびH₂分子モデルを使用しました。

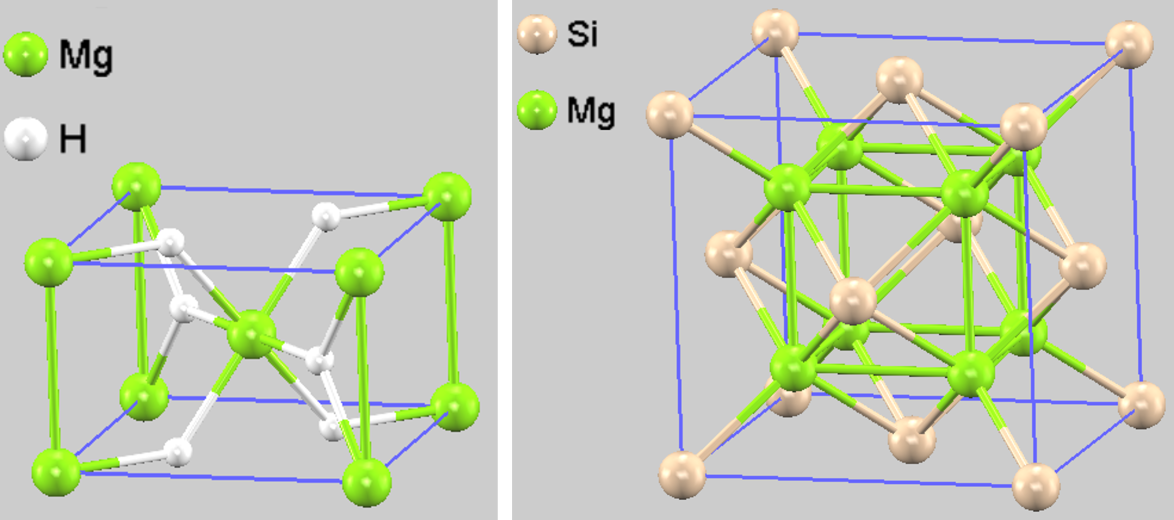
MgH2とMg2Siの計算セル
図1.　計算に用いた (左) MgH₂ と (右) Mg₂Si の計算セル

本解析で用いた主な計算条件は表1に示されています。

表1.　計算条件の概要

項目	設定
擬ポテンシャル	PAWポテンシャル
交換相関汎関数	GGA (PBE)
波動関数のカットオフエネルギー	25 Rydberg
k点サンプリング	セルサイズや金属性有無に応じて十分に設定

計算結果と考察#

最適化された格子定数#

MgH₂とMg₂Siの構造（図1）を最適化し、格子定数を算出しました。表2に示すように、本計算値（PBE）は実験値 [1] と文献値 (GGA-PW91を用いた計算値）[2] と良好な一致を示しており、計算の妥当性が確認できます。

表2. MgH₂とMg₂Siの最適化した格子定数 (単位: Å)

物質	項目	計算値 (PBE)	文献値(PW91)	実験値
MgH₂	a	4.522	4.466	4.517
MgH₂	c	3.022	2.992	3.021
Mg₂Si	a	6.360	6.361	6.390

水素放出エンタルピー#

次に、2つの反応のエンタルピー（ΔH）を算出しました。表3に示す値は、基準反応(A)と不安定化反応(B)を比較するため、すべてH₂ 1モルあたりの放出エンタルピー（単位: kJ/(mol H₂)、もしくはkJ/mol H₂）として正規化しています。

表3. 水素放出エンタルピー（ΔH）の比較 (単位: kJ/mol H₂)

反応	本計算 (PBE)	文献値 (PBE)	文献値 (PW91)	実験値 [1]
A. 基準反応 (MgH₂ → Mg + H₂)	55.64	55.3	65.1	70.6
B. 不安定化反応 (2MgH₂ + Si → ...)	31.89	31.4	37.9	-

考察#

基準反応（A）のエンタルピーは 55.64 kJ/mol H₂ であり、これは水素放出のためには高温を必要とする、比較的高い値です。一方、Si を添加した不安定化反応（B）では、エンタルピーが 31.89 kJ/mol H₂ へと劇的に低下しました。この結果は、H₂放出後に残ったMgがSiと反応して Mg₂Si という非常に安定な化合物を形成することで、H₂放出が熱力学的に有利になる（不安定化する）という概念を明確に裏付けています。本計算で用いたPBE汎関数による計算値は、文献 [2] のPBE計算値と非常によく一致しています。汎関数の種類（PBEとPW91）によってΔHの絶対値は異なりますが、Siの添加によって水素放出エンタルピーが大幅に低下するという物理的な傾向は、VajoらによるSi添加系での実験報告 [3] とも整合的であり、添加剤による不安定化効果の妥当性を示しています。

まとめ#

本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、金属水素化物MgH₂の水素放出エンタルピーに対する添加剤（Si）の効果を評価しました。計算の結果、添加剤なしの基準反応 (MgH₂ → Mg + H₂) のエンタルピーが 55.64 kJ/mol H₂ であるのに対し、Si を添加した不安定化反応 (2MgH₂ + Si → Mg₂Si + 2H₂) では 31.89 kJ/mol H₂ へと大幅に低下することが示されました。これは、Siを添加することで H₂ 放出後に安定な Mg₂Si が生成されるため、熱力学的に水素が放出されやすくなる（不安定化する）ことを定量的に示しており、第一原理計算が水素貯蔵材料の設計において強力なツールであることを示しています。

参考文献#

D. R. Lide (Ed.), CRC Handbook of Chemistry and Physics, 83rd ed., CRC Press, New York, 2002.
S. V. Alapati, J. K. Johnson, and D. S. Sholl, "Identification of destabilized metal hydrides for hydrogen storage using first principles calculations", J. Phys. Chem. B 110, 8769 (2006).
J. J. Vajo, F. Mertens, C. C. Ahn, R. C. Bowman, Jr., and B. Fultz, "Altering Hydrogen Storage Properties by Hydride Destabilization through Alloy Formation: LiH and MgH₂ Destabilized with Si", J. Phys. Chem. B 108, 13977 (2004).

金属水素化物MgH2不安定化の第一原理計算: 添加剤による水素放出促進効果#