コンテンツにスキップ

遷移金属ドープウルツ鉱型半導体の磁気特性の第一原理解析#

次世代の超低消費電力・高機能デバイスの実現を目指す「スピントロニクス」分野では、半導体に磁性を付与した「希薄磁性半導体」が重要な役割を担います。本稿では、第一原理計算ソフトウェアAdvance/PHASEを用い、代表的なウルツ鉱型半導体に磁性を持つ遷移金属をドープした系の磁気特性と電子状態を解析する事例を通じて、計算科学が材料設計にどのように貢献するかを解説します。

Keywords: 第一原理計算, 希薄磁性半導体, スピントロニクス, ハーフメタル, GaN

計算モデルの構築#

本解析では、代表的な半導体である窒化ガリウム(GaN)に、磁性を持つ遷移金属であるバナジウム(V)を不純物として導入した系を考えます。このような材料は希薄磁性半導体と呼ばれます [1-2]。実在の材料に近い状態をシミュレーションするため、まずGaNの基本構造（ウルツ鉱型構造）を複数個並べた「スーパーセル」という大きな計算モデルを用意します。そして、スーパーセル内の一部のGa原子をV原子で置き換えることで、Vが6.25%ドープされた (Ga,V)N モデル（組成式: Ga30V2N32）を構築しました（図1）。

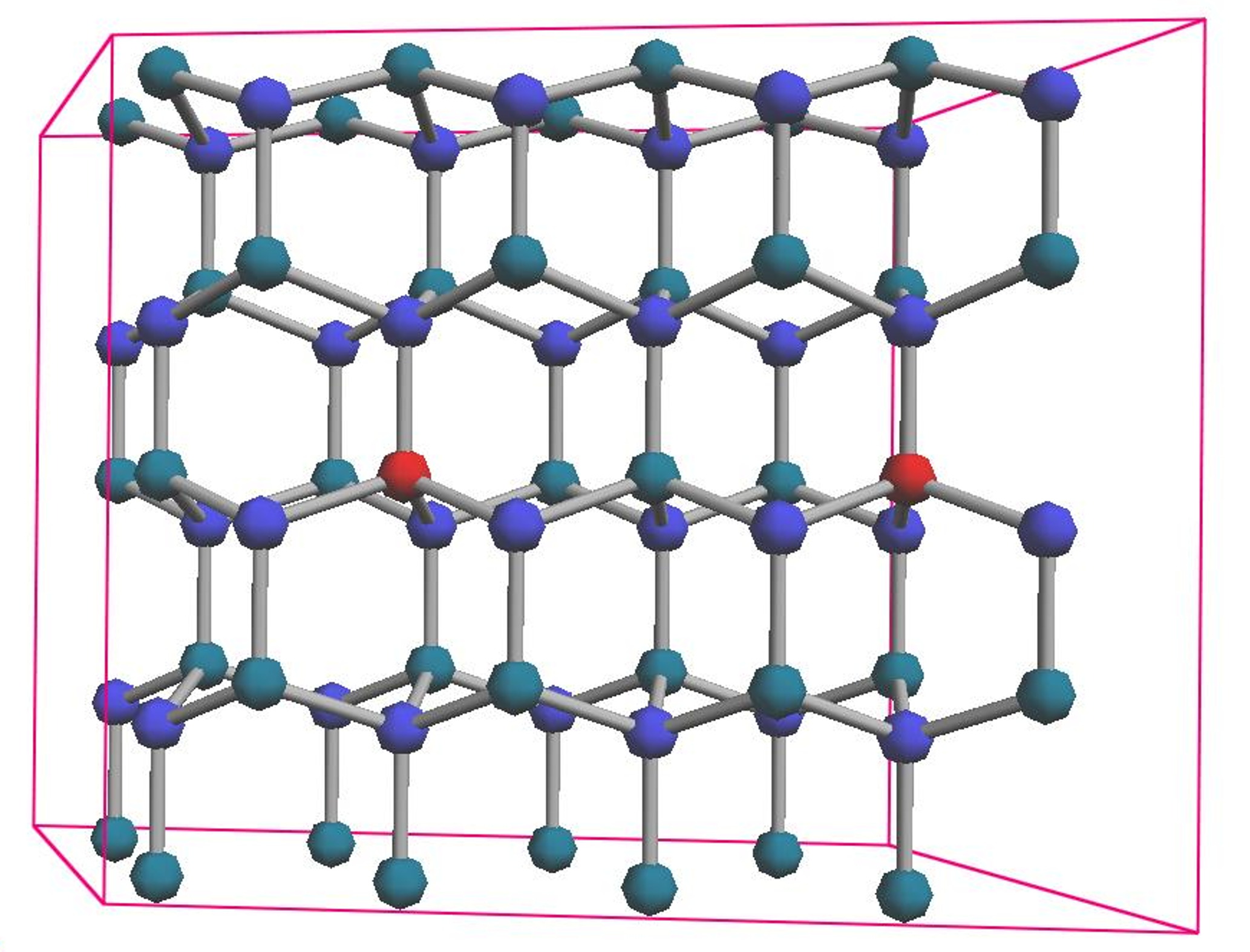
図1　計算モデル (Ga30V2N32)。赤球が磁性を担うV原子。

磁気的安定性の評価#

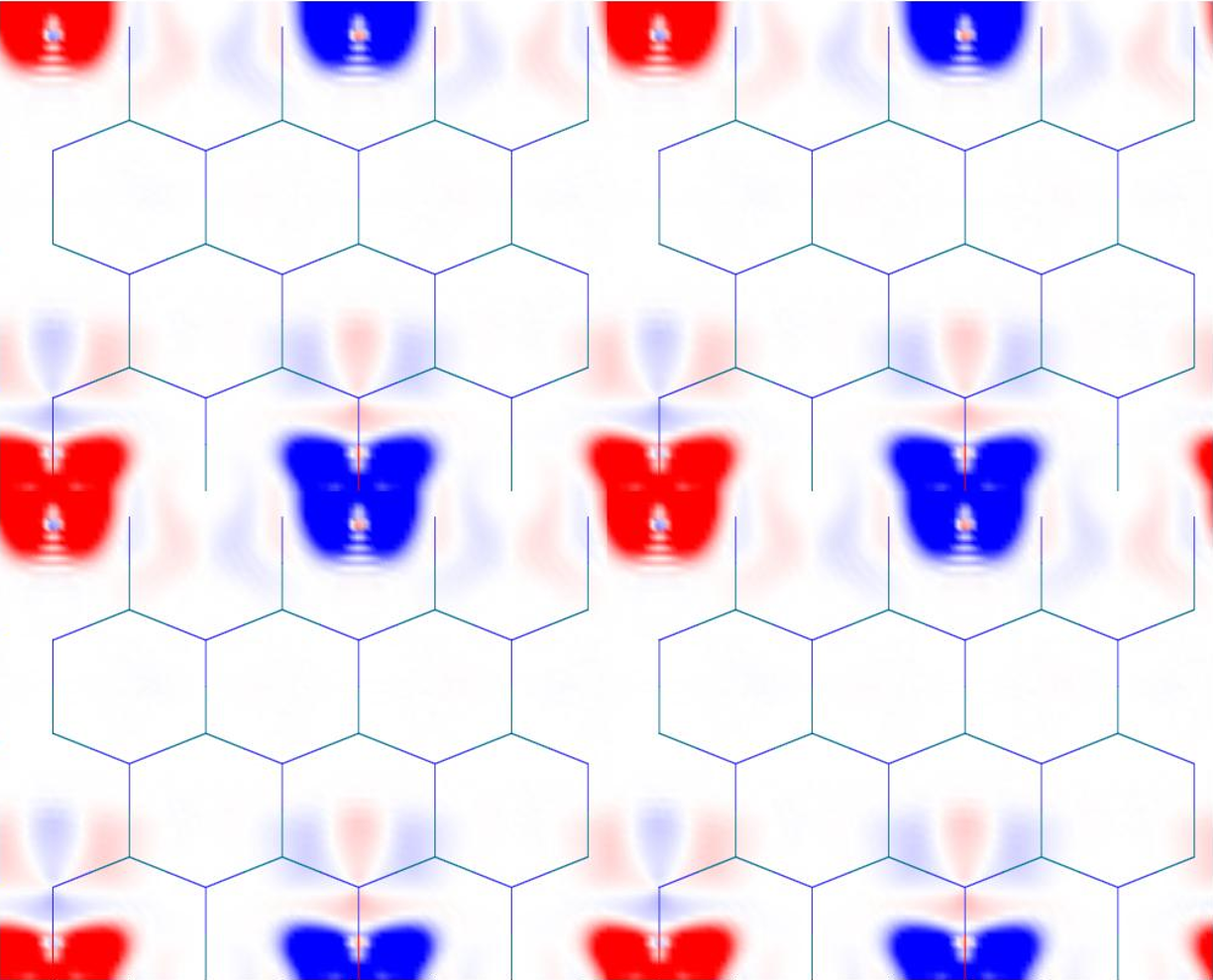
磁性材料として機能するためには、物質全体でスピンの向きが自発的に揃う強磁性が、最も安定な状態でなければなりません。そこで、①V原子のスピンが全て同じ向きに揃った「強磁性(FM)状態」（図2）と、②スピンの向きが互い違いになった「反強磁性的(AFM)状態」（図3）の2つのモデルについて全エネルギーを計算し、どちらが安定かを比較しました。

表1　磁気状態の安定化エネルギー

磁気状態 エネルギー差 (ΔE)
強磁性 (FM) -3.1 meV (最も安定)
反強磁性(AFM) (基準) 0 meV

計算の結果、強磁性状態は反強磁性状態に比べて3.1 meVだけエネルギーが低いことが分かりました。このエネルギー差 (安定化エネルギー) が、V原子のスピンを同じ向きに揃えさせる力の源泉です。これにより、この材料は外部から磁場をかけなくても自発的に磁石の性質（強磁性）を示す、安定な磁性半導体であることが理論的に示されました。

強磁性状態のスピン分極
図2　強磁性(FM)状態のスピン分極密度。V原子の周りに同じ向きのスピン（赤い分布）が局在。
反強磁性状態のスピン分極
図3　反強磁性(AFM)状態のスピン分極密度。V原子のスピン（赤と青の分布）が逆向きになっている。

電子状態解析#

次に、電子状態を解析しました。図4はこの材料の状態密度(DOS)を示したものです。物質の電気伝導特性は、フェルミ準位（, エネルギー0 eV）付近に、電子が占有できる状態が存在するかによって決まります。

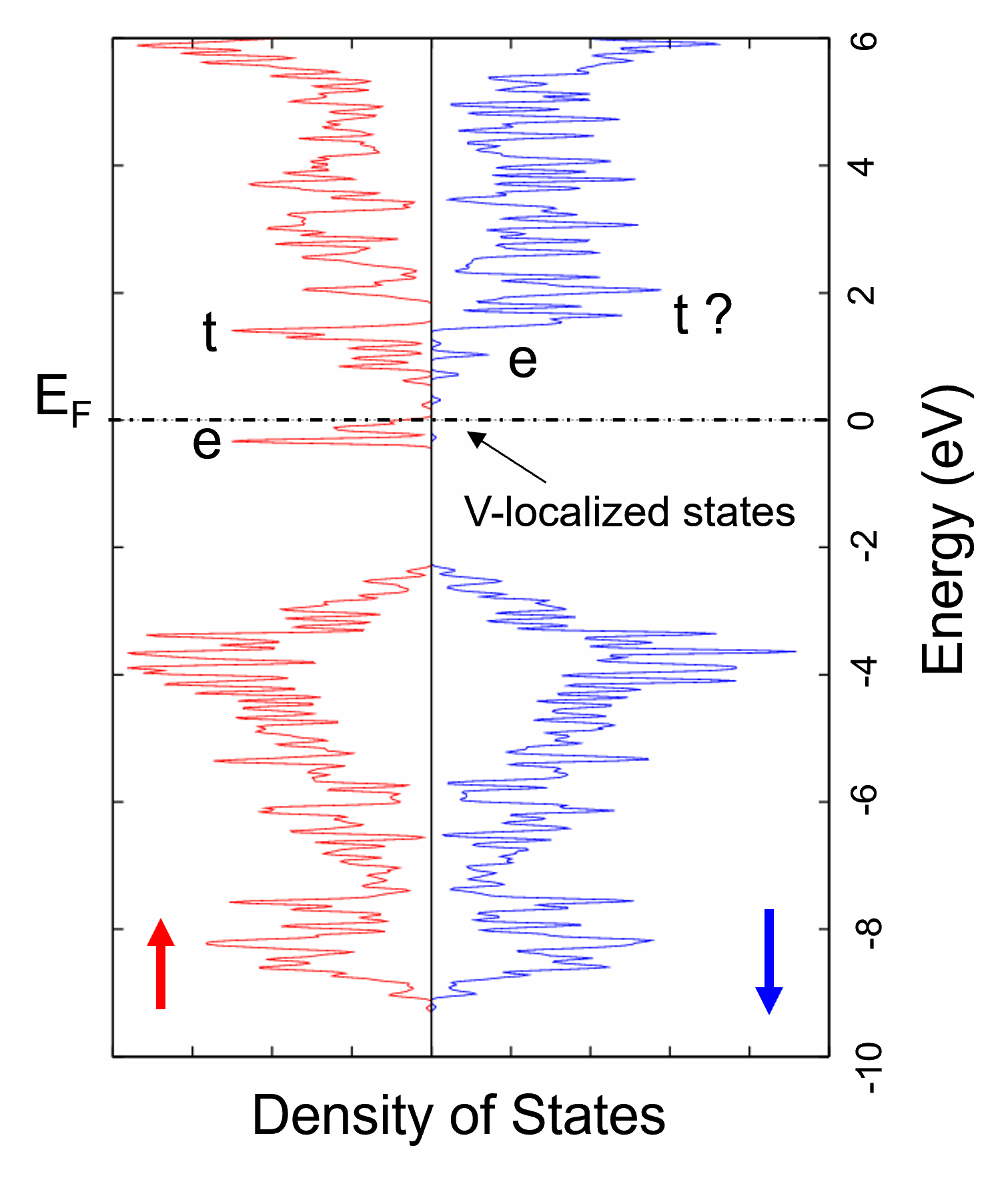
図4　状態密度(DOS)。電気伝導を担うフェルミ準位(0 eV)で、スピンアップ電子とダウン電子の挙動が全く異なる。

状態密度の詳細：結晶場分裂と局在状態#

図4のグラフを詳しく見ると、 V-localized states、 t、 e というラベルがあります。これらは磁性の起源を物理的に説明する重要な概念です。

  • V-localized states (V原子の局在状態): このエネルギー領域の電子が、結晶全体に広がらず、主にV原子の周りに強く束縛されていることを示します。この局在した電子がスピンを持つことで、物質全体の磁性が生まれます。

  • t, e (結晶場分裂): V原子のような遷移金属が結晶の中に入ると、周囲の原子（ここでは窒素N）が作る電場（＝結晶場）の影響で、エネルギーが同じだった5つの3d軌道が複数のグループに分裂します。この現象を結晶場分裂と呼びます。GaNの結晶構造では、3d軌道はエネルギーが高い3つの軌道群（t状態）と、エネルギーが低い2つの軌道群（e状態）に分裂します。図4は、V原子の局在状態が、さらにこの結晶場分裂によってt状態とe状態に分かれている様子を正確に描き出しています。

ハーフメタル性の発現とその解釈の難しさ#

この電子状態がもたらす最も重要な特性として、しばしば「ハーフメタル性」が議論されます。図4に示した状態密度は、一般的なGGA法による計算結果であり、一見すると理想的なハーフメタルの特性を示唆しています。

  • スピンアップ電子（赤線）: フェルミ準位に多数の状態が存在し、金属のように電気を通すように見えます。

  • スピンダウン電子（青線）: フェルミ準位に状態が無く、半導体（絶縁体）のように電気を通さないように見えます。

しかし、希薄磁性半導体におけるハーフメタル性の予測は、電子間の強い反発（クーロン相互作用）をどう扱うかという計算手法の詳細に大きく依存することが知られています。例えば、より精密な手法であるGGA+U法を用いると、このハーフメタル性は失われ、物質は絶縁体的な振る舞いを示すという研究報告もあります [3]。

このことは、第一原理計算が物性予測の強力なツールであると同時に、その結果を解釈する上で計算手法の選択とその影響を深く理解する必要があることを示しています。

まとめ#

本稿では、第一原理計算ソフトウェアAdvance/PHASEを用い、遷移金属をドープしたウルツ鉱型半導体の磁気物性を詳細に解析しました。その結果、この材料は安定な強磁性を示すことが理論的に確認できました。一方で、スピントロニクス応用で重要となるハーフメタル性については、その予測の難しさも浮き彫りになりました。標準的な計算ではハーフメタル性が示唆されるものの、より精密な手法では絶縁体へと変化する可能性も報告されており、理論的な材料設計の課題と奥深さを示しています。

参考文献#

  1. K. Sato and H. Katayama-Yoshida, "First-principles materials design for semiconductor spintronics", Semicond. Sci. Technol. 17, 367 (2002).

  2. K. Sato et al., "First-principles theory of dilute magnetic semiconductors", Rev. Mod. Phys. 82, 1633 (2010).

  3. G. Yao et al., "First-principles analysis on V-doped GaN", Optical Materials 34, 1593 (2012).

関連ページ#