磁気異方性エネルギーの第一原理計算#

磁気異方性エネルギーは、物質が特定の方向に磁化しやすい性質（磁気異方性）の強さを示す重要な物理量です。このエネルギーは主に、電子のスピンと軌道運動の相互作用（スピン軌道相互作用）に起因します。本解析では、第一原理計算ソフトウェアAdvance/PHASEを用いて、磁性体であるL1₀型合金とCo/Pt人工格子の磁気異方性エネルギーを定量的に評価し、その有効性を示します。

Keywords: First-principles calculation, spin-orbit interaction, magnetic anisotropy energy, L1₀-type alloy, superlattice

理論的背景#

スピン軌道相互作用エネルギーの計算には、Advance/PHASEで採用されているPAW（Projector Augmented-Wave）法 [1] を用いました。PAW法における全電子波動関数 $|\Psi\rangle$ は、計算コストの低い擬波動関数 $|\tilde{\psi}\rangle$ を基に、原子核近傍のコア領域で全電子原子軌道 $|\phi^{\text{AE}}\rangle$ と擬原子軌道 $|\tilde{\phi}^{\text{PS}}\rangle$ の差分を補正することで表現されます。

$|\Psi_{\nu}\rangle = |\tilde{\psi}_{\nu}\rangle + \sum_{I,m} \left(|\phi^{\text{I,AE}}_{m}\rangle - |\tilde{\phi}^{\text{I,PS}}_{m}\rangle\right) \langle\tilde{\beta}^{I}_{m}|\tilde{\psi}_{\nu}\rangle$

ここで、添字の $I$ は原子サイト、 $m$ は各サイトの原子軌道の量子数を表しています。また、添字 $\nu$ はバンドインデックスとスピンをまとめた複合的なインデックスです。 $\langle\tilde{\beta}^{I}_{m}|$ はプロジェクター関数と呼ばれ、擬波動関数 $|\tilde{\psi}_{\nu}\rangle$ のうち、原子サイト $I$ のコア領域成分を抽出する役割を担います。

スピン軌道相互作用を表すハミルトニアン $H_{\text{soc}}$ は、電子の軌道角運動量 $\mathbf{L}$ とスピン角運動量 $\mathbf{S}$ の結合として、次のように表されます。

$H_{\text{soc}} = \zeta(r) (\mathbf{L} \cdot \mathbf{S})$

ここで、相互作用の強さを表す $\zeta(r)$ は、原子核が作る球対称ポテンシャル $V(r)$ の勾配に比例し、

$\zeta(r) \propto \frac{1}{r}\frac{dV(r)}{dr}$

という形で原子核にごく近い領域で非常に強くなるという特徴があります。

このハミルトニアンの期待値 $\langle H_{\text{soc}} \rangle$ は、PAW法の枠組みにおいて、相互作用が最も顕著なコア領域 ( $\Omega$ ) からの寄与が支配的であると近似して計算されます。本解析では、このコア領域内の全電子原子軌道のみを考慮し、かつスピンの方向を量子化軸方向に限定する「コリニア磁性」の近似の下で計算を行いました。

$\langle H_{\text{soc}} \rangle \approx \sum_{ij} \rho_{ij} \langle \phi^{\text{AE}}_{i} | H_{\text{soc}} | \phi^{\text{AE}}_{j} \rangle_{\Omega}$

計算例#

L1₀型合金#

L1₀型構造を持つ合金は、ハードディスクなどの高密度磁気記録材料として重要であり、高い磁気異方性エネルギー（MAE）を示すことで知られています。この特性は、図1のように2種類の金属元素（A, B）がc軸 (001方向) に沿って交互に積層する結晶構造の異方性に由来します。

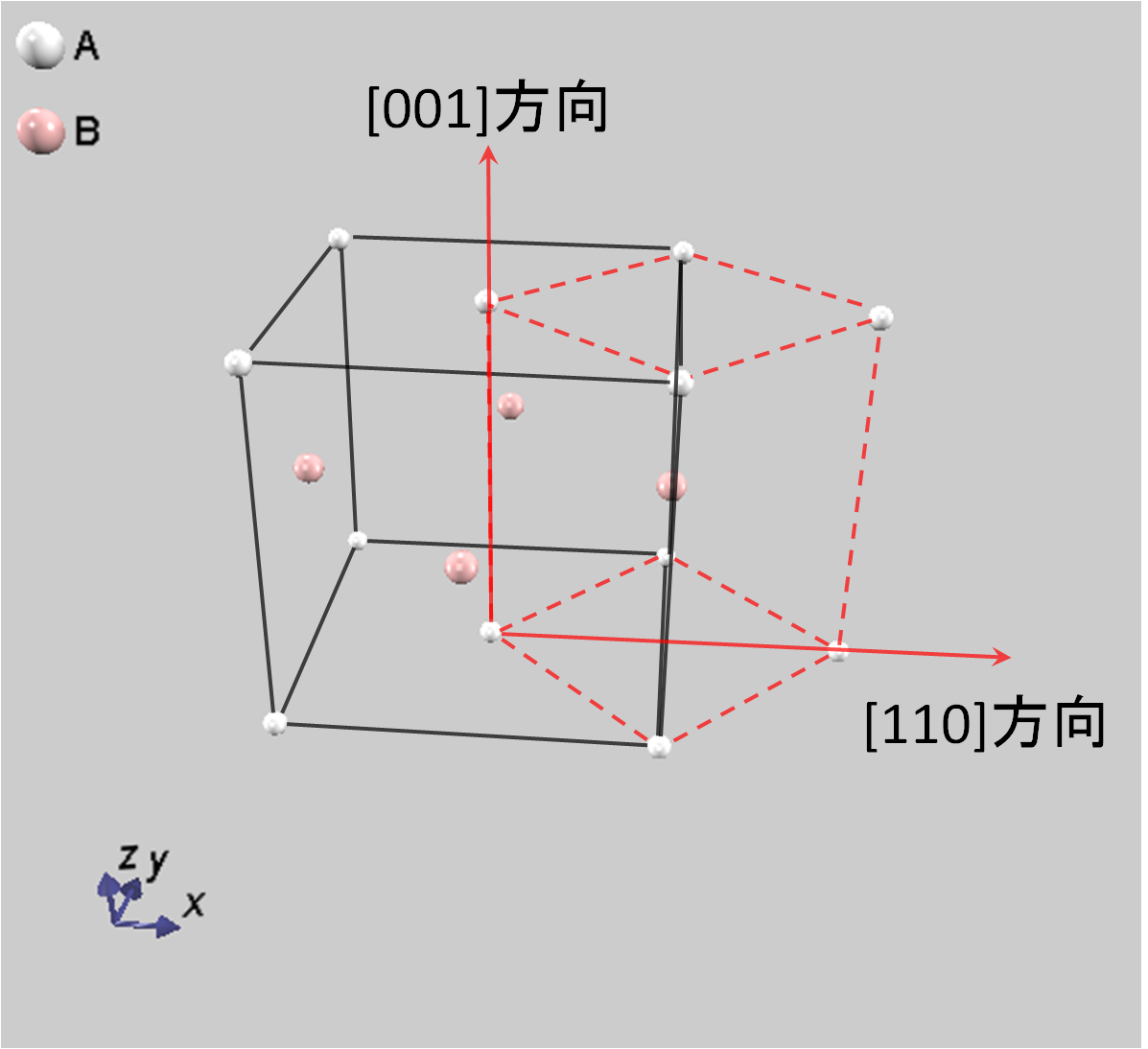
図1．L1₀型合金の結晶構造。

ここでは、代表的なL1₀型合金の中から、強磁性を示すFePt, FePd, FeNi、および反強磁性を示すMnPt, MnPdを計算対象とし、以下の計算条件でMAEを評価しました。

擬ポテンシャル： PAW（セミコア含む）
k点サンプリング： 24×24×24メッシュ（Mn系は24×24×12）
波動関数カットオフ： 40 Rydberg
電荷密度カットオフ： 400 Rydberg

計算には[001]および[110]方向をスピン量子化軸として、スピン軌道相互作用を含むSCF計算を実施します。全エネルギーの計算値から、安定なスピン量子化軸の方向、および2状態間のエネルギー差つまり磁気異方性エネルギーが決定されます（MAE = E[110] - E[001]）。この計算で得られた各種L1₀型合金の MAE を、全電子計算 [2] や実験値と比較した結果を表1に示します。

表1．L1₀型合金の磁気異方性エネルギー (単位: meV)

磁性	Advance/PHASE	全電子計算	実験値	磁化容易軸
FePt (強磁性)	2.797	2.891	0.881	[001]
FePd (強磁性)	0.424	0.342	0.520	[001]
FeNi (強磁性)	0.172	0.172	0.254	[001]
MnPt (反強磁性)	4.311	5.342	-	[001]
MnPd (反強磁性)	0.651	0.147	-	[001]

表1から、本手法（Advance/PHASE）による計算値は、解析した全てのL1₀型合金において正のMAEを与えていることがわかります。これは、磁化容易軸がc軸方向（[001]）であることを意味しており、実験的に知られている事実を正しく再現しています。

ここで特筆すべきは、磁気異方性エネルギー（meVオーダー）が、計算で得られる全エネルギー（数千eVオーダー以上）に比べて100万分の1以下と極めて小さい値であるという点です。このような膨大な数値の中から微小なエネルギー差を安定して求めることは、計算手法に高い精度と安定性が要求される挑戦的な課題です。

その上で表1の値を評価すると、FePdやFeNiでは実験値や全電子法の結果と定量的によく一致しています。FePtやMnPtのように値の大きさに差が見られるケースもありますが、巨大な一軸磁気異方性を持つという物性の本質的な傾向は正確に捉えられています。

Co/Pt人工格子#

Co/Ptを積層させた人工格子は、膜面に対して垂直方向に磁化しやすい「垂直磁気異方性」を持ちます [3] 。この特性は、ハードディスクなどの高密度な垂直記録方式において極めて重要な役割を果たしています。計算モデルとして、図2で示したように、CoとPtを[111]方向に3原子層ずつ積層したユニットセル（Co3/Pt3）を用いました。MAEは、スピン量子化軸を膜に垂直なz軸と、面内のx軸にとった場合のエネルギー差として評価しました。

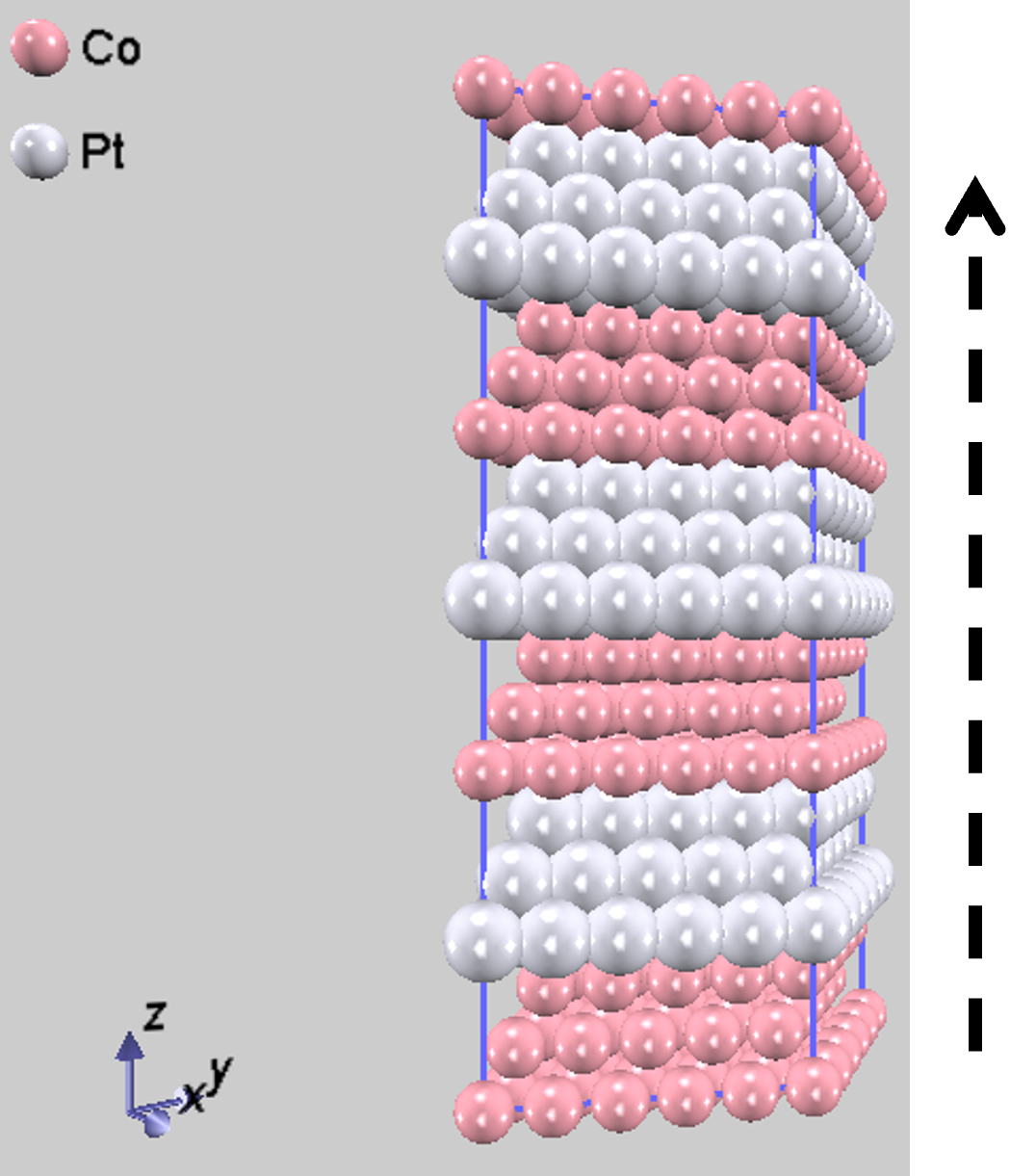
図2．Co/Pt人工格子の結晶構造。矢印は磁化容易軸を示しています。

計算条件は以下の通りです。

擬ポテンシャル： PAW
k点サンプリング： 16×16×8メッシュ
波動関数カットオフ： 40 Rydberg
電荷密度カットオフ： 400 Rydberg

計算の結果、MAE = 5.50 meVという大きな正の値が得られました。これはエネルギー的に垂直方向(z軸)が磁化容易軸であることを意味し、実験事実と一致します。Co 3d軌道の射影状態密度 (PDOS) の解析からは、磁気量子数 m=±1 の軌道がフェルミ準位近傍の状態密度に大きく寄与しており、その割合は45%に達することが判明しました。このような特定の軌道における電子状態の偏りが、スピン-軌道相互作用を通じて強い垂直磁気異方性を生み出す原因であると考えられます。

まとめ#

Advance/PHASEに実装されたコリニアスピン対応のスピン軌道相互作用計算機能を用いて、L1₀型合金およびCo/Pt人工格子の磁気異方性エネルギーを評価しました。計算結果は、全電子計算や実験値とも良い一致を示し、本手法が磁性体の磁気特性を定量的に評価する上で有効であることを示しています。特に、PAW法を用いることで計算が簡略化され、効率的に解析できることが特徴です。

参考文献#

P. E. Blöchl, Phys. Rev. B 50, 17953 (1994).
P. Ravindran et al., Phys. Rev. B 63, 144409 (2001).
P. F. Carcia, A. D. Meinhaldt, and A. Suna, Appl. Phys. Lett. 47, 178 (1985).