第一原理計算による固体の格子定数予測#
物質の結晶構造を特徴づける基本的なパラメータである格子定数は、その物質の特性と密接に関連しています。第一原理計算による格子定数の精密な予測は、新規材料の設計や物性解明において極めて重要です。しかし、計算精度は、採用する近似手法に依存します。特に、計算コストと精度のバランスを決定する「擬ポテンシャル」と、電子間の複雑な相互作用を取り扱う「交換相関汎関数」の選択は、結果に大きな影響を与えます。本解析では、第一原理計算ソフトウェアAdvance/PHASEを用いて、様々な元素・化合物からなる固体を対象とし、これらの計算条件が格子定数の予測精度にどのように影響するかを検証します。
Keywords: 第一原理計算, 格子定数, PAW, ウルトラソフト擬ポテンシャル, 交換相関汎関数
計算手法の概要#
密度汎関数理論（DFT）に基づき、エネルギー-体積曲線 (E-V曲線）で様々な固体の格子定数を算出しました。電子間の交換相関相互作用を記述する汎関数として、汎用性の高いGGA-PBE汎関数を共通して使用しました。その上で、内殻電子と原子核を一体として扱う擬ポテンシャルの種類を変え、結果を比較しました。
- PAW (Projector Augmented-Wave)法: 全電子計算の精度を保ちつつ、計算効率を高めた手法。現在、高精度計算の標準的な手法の一つとされています。
- ウルトラソフト(US)擬ポテンシャル法: 波動関数を滑らかにすることで、少ない波数で電子状態を表現可能にし、計算コストを大幅に削減する方法。これも標準的な手法として利用されています。
また、様々なGGA汎関数に基づいた計算には、計算セルの自動最適化機能を使用しました。
計算結果と考察#
擬ポテンシャルの種類による精度の比較#
図1と図2に、様々な元素・化合物に対して、それぞれPAWとウルトラソフト（US）擬ポテンシャルを用いて計算した格子定数を、実験値と比較したパリティプロットを示します。これらの実験値は、標準的な結晶構造データベースや学術文献から収集したものです。プロット中の点は各物質に対応し、対角線（y=x）上に乗るほど計算値と実験値が一致していることを意味します。なお、USを用いた評価では、主要な傾向を把握可能なサンプル数に絞り、計算コストを考慮して一部の計算を省略しました。
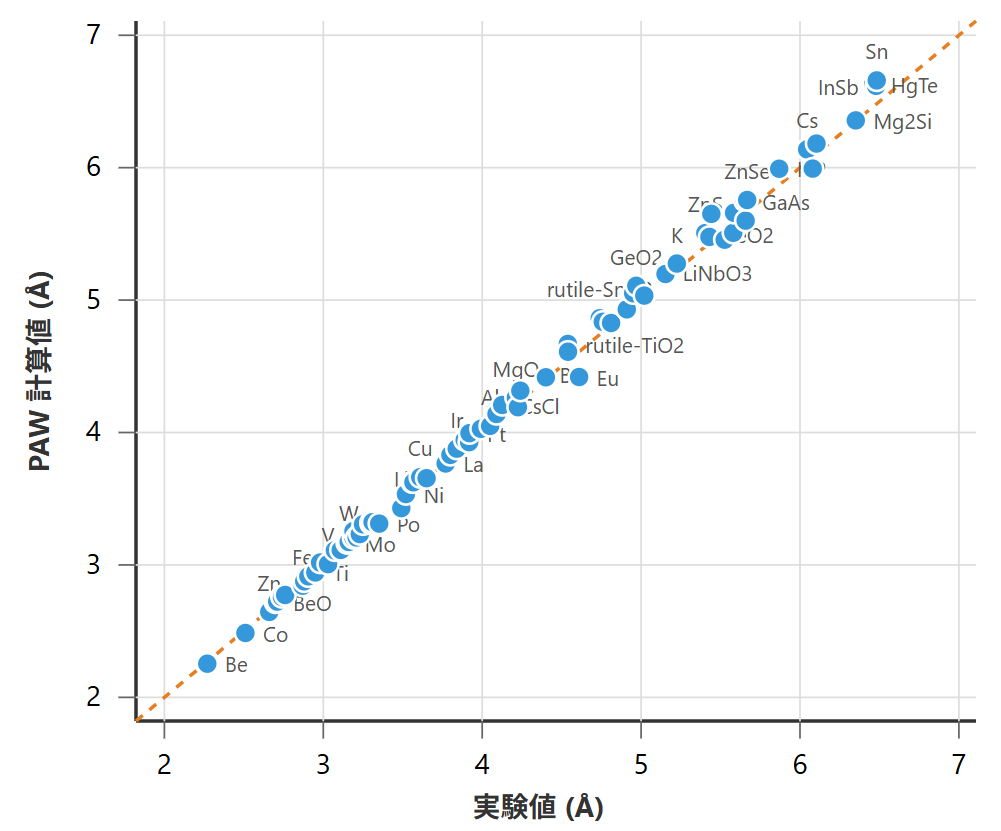
図1. PAW法による格子定数の計算値と実験値の比較（データ数：81）
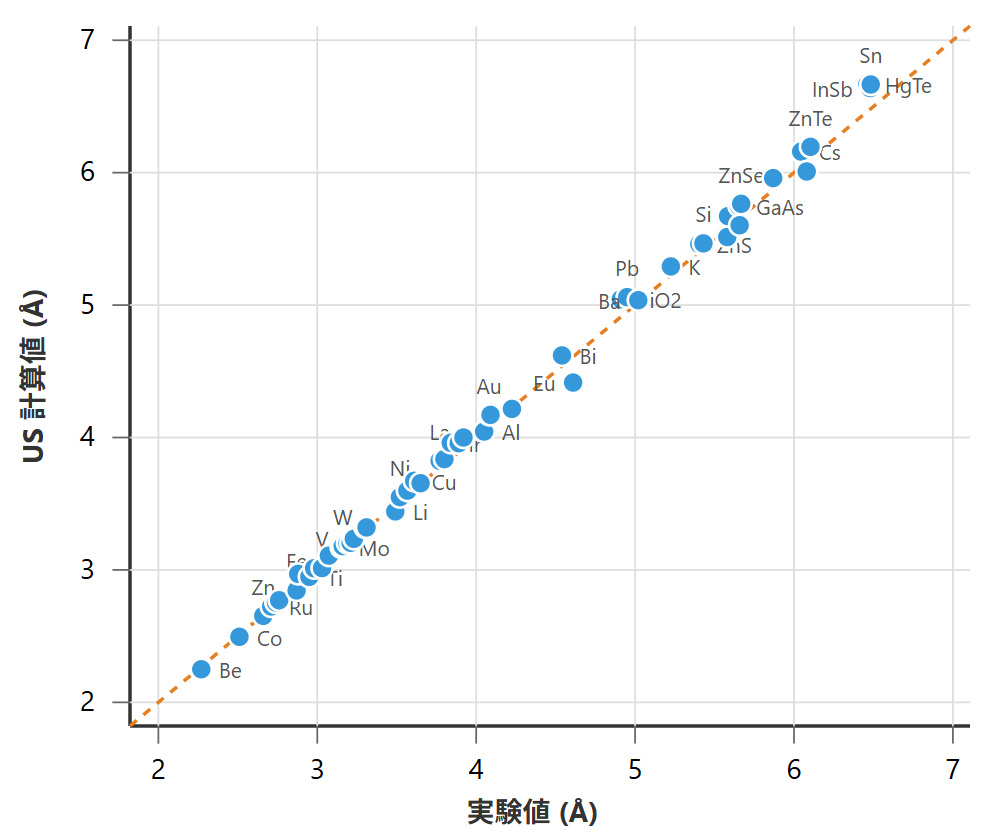
図2. ウルトラソフト擬ポテンシャル法による格子定数の計算値と実験値の比較（代表的な55種の物質群）
両手法とも、計算値と実験値の間に強い正の相関が見られ、全体として良好な予測精度を示しています。定量的な評価として、実験値に対する誤差を表1に示します。
表1. 擬ポテンシャルごとの計算誤差
| 評価指標 | PAW法 | ウルトラソフト(US)擬ポテンシャル法 |
|---|---|---|
| 平均絶対誤差 (MAE) | 0.054 Å | 0.057 Å |
| 平均絶対パーセント誤差 (MAPE) | 1.18 % | 1.26 % |
誤差指標を比較すると、PAW法の方がウルトラソフト擬ポテンシャル法に比べて平均誤差がわずかに小さいことがわかります。これは、PAW法が電子の波動関数の節（ノード）の情報を保持しているため、より物理的に忠実な記述が可能であることに起因します。しかし、その差は僅かであり、計算コストの観点から、ウルトラソフト擬ポテンシャルも依然として有効な選択肢であることが示唆されます。なお、本比較は代表的な物質群に対する性能の目安を示すものであり、両手法の厳密な優劣を決定するものではありません。
交換相関汎関数の影響と限界：水銀(Hg)の例#
上記の精度評価では、水銀(Hg)を除外しています。なぜなら、Hgの格子定数はGGA-PBE汎関数では実験値を大幅に過大評価（誤差+7.6%）してしまい、例外的に大きな誤差を与えるためです。これは、絶対零度において融点の低いHgが弱いファンデルワールス力（vdw force）で結合した固体であり、その物理的性質が電子の相関効果に強く影響されるためです。標準的なGGA汎関数は、このような長距離の電子相関を正確に記述することができず、結果として結合を弱く見積もり、格子定数を過大評価しまいます[1]。
このHgの例は、標準的な手法が常に万能ではないことを示す好例です。ファンデルワールス力で凝集する系や強相関電子系など、対象とする物質の物理的特性を理解し、場合によってはvdw-DFやDFT+U、ハイブリッド汎関数といった、より高度な計算手法を選択することの重要性を示唆しています。
より一般の場合でも、様々なGGA汎関数が開発されています。表2は、いくつかの代表的な金属（Pt, Au, W）の格子定数を、標準的なPBE、分子系・吸着系向けのrevPBE, RPBE, 固体向けのPBEsol, Wu-Cohen汎関数で計算した結果です。
表2. 様々な GGA 汎関数を用いて計算した結晶の格子定数 (単位：Å)
| 汎関数 | Pt (fcc, US) | Au (fcc, US) | W (bcc, US) | W (bcc, PAW) |
|---|---|---|---|---|
| PBE | 3.999 | 4.173 | 3.180 | 3.173 |
| revPBE | 4.015 | 4.200 | 3.181 | 3.190 |
| RPBE | 4.021 | 4.212 | 3.186 | 3.198 |
| PBEsol | 3.948 | 4.100 | 3.144 | 3.151 |
| Wu-Cohen | 3.959 | 4.111 | 3.151 | 3.157 |
| 実験値 | 3.923 | 4.079 | 3.166 | 3.166 |
この表から、固体の物性予測に特化して開発されたPBESol/Wu-Cohen汎関数が、汎用のPBE汎関数よりも実験値に近い値を与える傾向が読み取れます[2]。
計算における格子定数の扱いについて#
本解析では計算精度を評価するために格子定数の最適化を行いましたが、実際の研究では、実験値などを用い格子定数の最適化を省いて計算を進める場面も少なくありません。その背景には、主に以下の3つの理由が挙げられます。
- 計算値と実験値の差が小さい:
図1、図2に示した通り、標準的な手法を用いれば、第一原理計算は実験値と非常によく一致する格子定数を予測できます（平均誤差1.5%以内）。 - 物性への影響が比較的小さい:
電子バンド構造の全体的な形状や状態密度（DOS）、磁気的性質など、主に電子のエネルギー準位の相対的な関係で決まる物性は、格子定数の小さな変化に対して比較的鈍感です。そのため、これらの物性を議論する際には、計算コストをかけて格子定数を最適化するメリットが少なく、信頼できる実験値や文献値を参照点とする方が効率的です。ただし、弾性率や圧電定数など、その計算に平衡格子定数を参照して格子のひずみを算出する場合は、理論的な平衡格子定数を用いることが不可欠です[3]。 - 物理的に妥当な構造モデルの構築:
この理由は、特に不純物や表面吸着などの「局所的な乱れ」を含む系で重要になります。例えば、極微量の不純物が存在する結晶を考えましょう。実際の結晶は不純物の影響で格子定数が大きく変わることはありませんが、計算で用いる周期的境界条件とスーパーセルは、不純物が人工的に高濃度で配列した系として扱ってしまうことがあります。このモデルで不純物の濃度に応じて格子定数を最適化すると、現実の希薄な不純物系とは異なる結果を導き出してしまいます。このような場合、あらかじめ最適化した母材の格子定数を固定して計算する方が、バルク中に孤立した不純物という物理的に妥当な状況を正確に反映したモデルを構築できます[4]。
まとめ#
本解析では、第一原理計算ソフトウェアAdvance/PHASEを用いて、固体の格子定数計算における擬ポテンシャルと交換相関汎関数の選択が精度に与える影響を検証しました。擬ポテンシャルについては、PAW法がウルトラソフト法よりも若干改善を示しましたが、両方とも高い精度を達成しています。交換相関汎関数については、標準的なGGA汎関数が多くの物質で有効である一方、Hgのようなvdw結合系では限界があることを示しました。これにより、対象系の物理的特性に応じた手法選択の重要性が確認されました。また、計算モデルの目的や物理的な妥当性を考慮し、格子定数を固定するアプローチが有効な場合があることを示しました。第一原理計算を用いた材料シミュレーションにおいて、目的に応じて計算手法を適切に選択することで、信頼性の高い物性予測が可能となります。
参考文献#
- N. Gasto et al., "Lattice structure of mercury: Influence of electronic correlation", Phys. Rev. B 74, 094102 (2006).
- P. Haas, F. Tran, and P. Blaha, "Calculation of the lattice constant of solids with semilocal functionals", Phy. Rev. B 79, 085104 (2009).
- D. S. Sholl, and J. A. Steckel, Density functional theory: a practical introduction, John Wiley & Sons, 2022.
- C. Freysoldt et al., "First-principles calculations for point defects in solids", Rev. Mod. Phys. 86, 253 (2014).
関連ページ#
- 第一原理計算ソフトウェア Advance/PHASE
- 解析分野：ナノ・バイオ
- 産業分野：材料・化学