DFTによるdHvA効果の予測: アルカリ金属の例#

ドハース・ファンアルフェン効果(de Haas-van Alphen effect; dHvA効果)は、金属に強い磁場をかけ極低温に冷却した際に観測され、そのフェルミ面の形状を実験的に決定できる強力な手法です。固体物理学においてフェルミ面の形状は物質の電子的性質を支配する重要な要素であり、dHvA効果は第一原理計算(DFT)によるバンド理論の予測が正しいかを検証する強力な「ものさし」の一つとなっています。本解析では、第一原理計算ソフトウェアAdvance/PHASE を用い、代表的なアルカリ金属であるリチウム(Li)とカリウム(K)のフェルミ面を計算し、その形状の違いがどこから生じるのかを電子状態の観点から解明します。
Keywords: 第一原理計算, DFTシミュレーション, フェルミ面, dHvA効果, ドハース・ファンアルフェン効果, アルカリ金属, リチウム(Li), カリウム(K), バンド理論
予備知識:自由電子モデルとフェルミ面
ここで最も単純な金属のモデルである「自由電子モデル」について説明します。このモデルでは、金属内の価電子は、原子核(イオンコア)からのポテンシャルの影響を全く受けず、お互いの相互作用も無視して、箱の中を自由に飛び回っていると考えます。
量子力学によれば、電子の状態はその運動量(あるいは波数ベクトル )によって決まります。自由電子のエネルギー は、その運動エネルギーだけで決まり、以下の式で表されます。
ここで は電子の質量、 はディラック定数、 は波数ベクトルの大きさ(運動量空間の原点からの距離)です。
この式の重要な点は、エネルギー が波数ベクトル の「向き」( の比率)には一切依存せず、「大きさ」 だけで決まることです。
金属中の電子は、絶対零度ではエネルギーの低い状態から順に詰まっていきます。電子が詰まっている最も高いエネルギー準位をフェルミエネルギー()と呼びます。そして、運動量空間(k空間)において、エネルギーがちょうど になるような の点の集まりが作る曲面をフェルミ面と呼びます。
自由電子モデルの場合、フェルミエネルギー を持つ状態は を満たします。これを について解くと となり、 は一定の値(フェルミ波数)になります。
つまり、フェルミ面を構成する点は、k空間の原点からあらゆる方向に対して「等しい距離 」にある点の集まりとなります。これは、まさしく「球体」の定義そのものです。この理由により、自由電子モデルのフェルミ面がフェルミ球とも呼ばれます。
計算モデルと計算条件#
計算モデルとして、LiとKの体心立方格子(bcc)構造を用いました。フェルミ面の計算手順はバンド計算と似ていますが、フェルミ面の描画に必要なk点メッシュの設定は、バンド図(高対称線)の計算とは異なり、ブリルアンゾーン全体をカバーする高密度なメッシュが必要となります。
本解析で用いた主な計算条件は表1に示されています。
表1. 計算条件の概要
| 項目 | 設定 |
|---|---|
| ポテンシャル | PAWポテンシャル |
| 交換相関汎関数 | GGA (PBE) |
| 波動関数のカットオフエネルギー | 25 Rydberg |
| k点数 (フェルミ面描画用) | 約3.6万点 |
計算結果と考察#
リチウム (Li) のフェルミ面#
図1にLi (bcc) のフェルミ面を示します。外側の青い枠はbcc構造の第一ブリルアンゾーン(菱形十二面体)を示し、内側の黄色い曲面が計算されたフェルミ面です。自由電子モデルの完全な球形とは異なり、ブリルアンゾーンの境界(N点)に向かって膨らんだ(歪んだ)形状をしています。ここでN点とは、ブリルアンゾーンを構成する12個の菱形の面の中心点を指します。
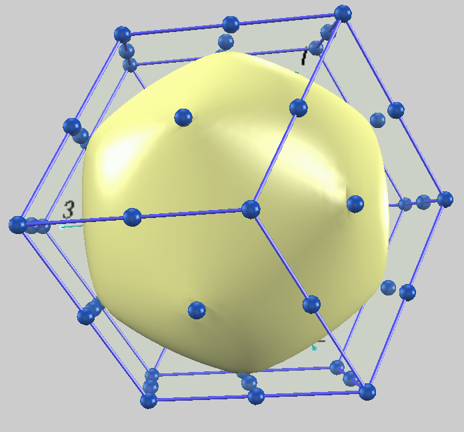
図1. Li (bcc) のフェルミ面(黄色い曲面)。外側の青い枠がブリルアンゾーンを示します。
カリウム (K) のフェルミ面#
次に、図2にK (bcc) のフェルミ面を示します。Liとは対照的に、Kのフェルミ面はほぼ理想的な球形をしていることがわかります。これは、Kの価電子が「自由電子」に非常に近い振る舞いをしていることを示唆しています。
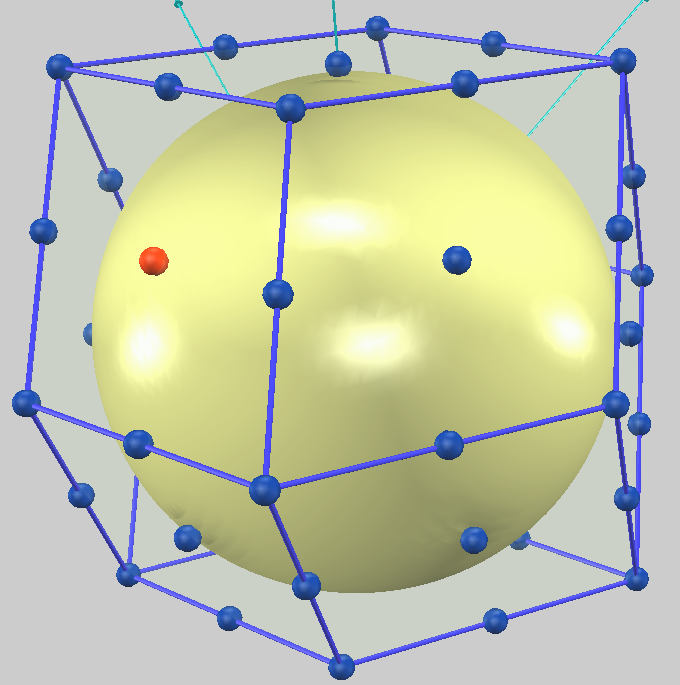
図2. K (bcc) のフェルミ面。Li(図1)とは異なり、フェルミ面はほぼ理想的な球形を保っています。
考察:フェルミ面の形状と実験結果の比較#
今回の計算結果は、dHvA効果の実験結果と非常によく一致しています。実験では、K(カリウム)はどの角度から測定しても、ほぼ1種類の単純な振動周期が観測され、これはフェルミ面が「球」であることを意味します。一方、Li(リチウム)は測定する角度によって振動周期が変化し、これはフェルミ面が球から「歪んでいる」ことを明確に示しています [1-3]。
では、LiとKは同じアルカリ金属・同じbcc構造でありながら、なぜフェルミ面の形状がこれほど異なるのでしょうか。その原因は、価電子が感じる「イオンコアからのポテンシャル」の強さにあります。
-
Li(リチウム): フェルミ面の異方性
Liのイオンコアは電子配置であり、p状態のコア電子(内殻p軌道)を持ちません。価電子バンド(主に原子の2s軌道から形成)は、ブリルアンゾーンのN点(方向)に近づくにつれて、その波動関数がp対称性(p-like character)を強く帯びます。しかし、コアにp状態が存在しないため、価電子がp対称性を帯びても、パウリの排他原理に基づく内殻軌道との直交性に起因する強い斥力ポテンシャル(擬ポテンシャル理論における斥力項)が働きません。結果として、イオンコアが持つ本来の強いクーロン引力が有効に遮蔽されず、N点におけるエネルギー準位が点(s対称)に比べて低下(安定化)します。フェルミエネルギー は一定であるため、エネルギー準位が低いN点方向には、より大きな波数ベクトル まで電子が充填されます。これが、フェルミ面がN点に向かって歪み、外側に膨らむ直接的な原因です。
-
K(カリウム): フェルミ面の等方性
一方、Kのイオンコアは大きく、2p軌道や3p軌道など、完全に占有された内殻p軌道を豊富に持ちます。Liと同様に、価電子バンド(主に4s軌道から形成)がN点近傍でp対称性を帯びると、これらの内殻p軌道と直交することが量子力学的に要請されます。パウリの排他原理に基づき、この直交化の条件は、価電子に対して強い斥力ポテンシャルとして作用します。Kの場合、このp対称性に対する強い斥力ポテンシャルが、イオンコアのクーロン引力と極めて効果的に相殺されます。その結果、価電子が感じる有効ポテンシャル(擬ポテンシャル)は非常に弱くなり、価電子はポテンシャルの影響をほとんど受けない「自由電子」(nearly-free electron)に近い振る舞いを示します。エネルギーが波数ベクトルの向き にほとんど依存せず、その大きさ だけで決まるため、フェルミ面は自由電子モデルに近い、ほぼ理想的な球形を維持します。
まとめ#
本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、アルカリ金属であるLi (bcc)とK (bcc) のフェルミ面を計算しました。計算結果は、Kが自由電子モデルに近い理想的な球形であるのに対し、LiはブリルアンゾーンのN点に向かって膨らんだ(歪んだ)形状を持つことを明瞭に示しました。この形状の違いは、Liの価電子が感じる強いイオンコアポテンシャルに起因し、その結果として-方向のバンドが引き下げられるためであることを電子状態の観点から説明しました。本計算結果は、dHvA効果による実験的な観測結果とも整合的であり、第一原理計算(DFT)が物質の基本的な電子的性質を高い精度で予測できる強力なツールであることを示しています。
本解析の詳細や、研究への適用可能性に関するご相談はこちら
お問い合わせ参考文献#
- J. J. Donaghy and A. T. Stewart, "Fermi surface of lithium by positron annihilation", Phys. Rev. 164, 391 (1967).
- N. W. Ashcroft and N. D. Mermin, Solid State Physics, Holt, Rinehart and Winston (1976).
- D. Shoenberg, Magnetic Oscillations in Metals, Cambridge University Press (1984).
関連ページ#
- 第一原理計算ソフトウェア Advance/PHASE
- 解析分野:ナノ・バイオ
- 産業分野:材料・化学