コンテンツにスキップ

第一原理計算による金属のフェルミ面の解析#

金属の電気伝導や磁性といった電子物性は、フェルミエネルギー近傍の電子状態によって支配されます。波数空間において、絶対零度で電子が占有する状態と占有しない状態を分ける境界をフェルミ面と呼び、その形状は「金属の顔」として物質の個性を決定づける極めて重要な物理量です。本解析では、第一原理計算ソフトウェアAdvance/PHASEを用いて、代表的な金属である銅（Cu）、マグネシウム（Mg）、鉄（Fe）のフェルミ面を計算し、それぞれの電子構造の特徴を明らかにします。

Keywords: 第一原理計算, フェルミ面, 電子状態, Cu, Mg, Fe, 強磁性

計算方法#

フェルミ面の計算は、以下の手順で行います。

  1. 構造モデルの準備: 計算対象となる結晶のprimitive cell（基本単位胞）を用意します。Conventional unit cell（慣用単位胞）でも計算は可能ですが、逆格子空間でのブリルアンゾーンが複雑になるため、通常はprimitive cellを用いるのが標準的かつ効率的です。

  2. SCF計算: まず、通常のSCF（Self-Consistent Field）計算を行い、系の基底状態における電子密度とフェルミエネルギーを決定します。強磁性Feの計算には、スピン分極をあらわに考慮します。

  3. フェルミ面計算用のnon-SCF計算: 次に、フェルミ面を描画するため、非常に多くのk点における固有エネルギーを求めるnon-SCF計算を実行します。この際、バンド構造計算のように特定の対称線上だけでなく、ブリルアンゾーン全体を網羅する高密度なk点メッシュを生成し、計算に用います。

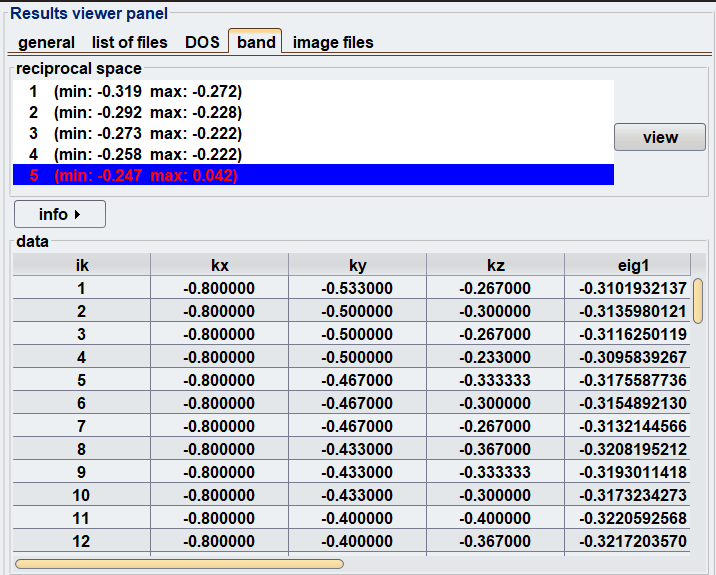
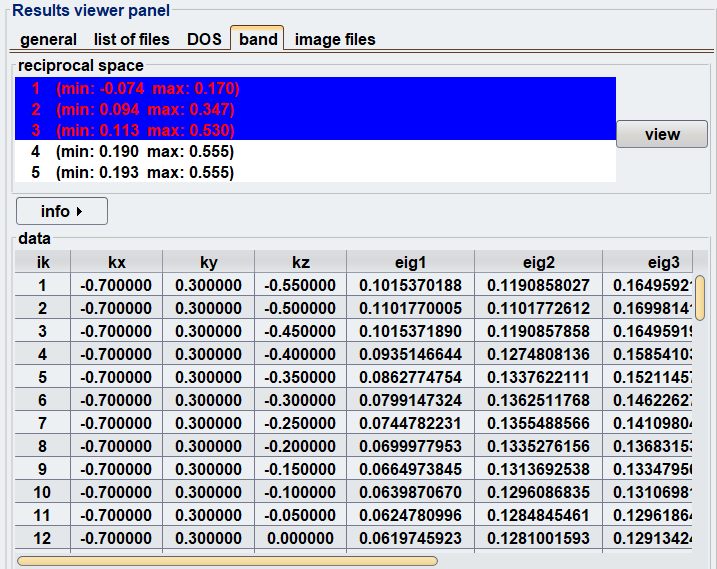
  4. 可視化: 計算後、Advance/PHASEのGUI機能を用いてフェルミ面を可視化します。GUIは、計算された全バンドの中からフェルミエネルギーを横切るバンドを自動的に検出し、「赤いバンド」としてリストアップします。これらの赤いバンドをすべて選択するだけで、対応するフェルミシートが描画され、物質全体のフェルミ面が得られます（図1）。

銅(Cu)のバンドデータ
図1(a) 銅(Cu)のバンドデータ例。1本のバンド（赤色）がフェルミ準位を横切ります。
マグネシウム(Mg)のバンドデータ
図1(b) マグネシウム(Mg)のバンドデータ例。複数のバンド（赤色）がフェルミ準位を横切ります。

解析結果と考察#

本解析では、1価金属（Cu）、2価金属（Mg）、そして強磁性金属（Fe）という、それぞれ特徴の異なる3つの金属を対象にフェルミ面の計算を行いました。これらの金属のフェルミ面が文献でよく知られています [1-4]。

1. 銅 (Cu) - 1価金属の典型例#

1価の金属である銅（Cu）は、価電子が比較的自由に振る舞うため、そのフェルミ面は自由電子モデルで予測される球形に近いことが知られています。計算では、フェルミエネルギーを横切るバンドは1本でした。図2に示すように、計算されたフェルミ面は全体として球に近いですが、ブリルアンゾーンの境界（<111>方向）に向かって「ネック」と呼ばれる突起が伸びていることがわかります。これは結晶格子ポテンシャルの影響を反映したものであり、文献で知られる銅のフェルミ面の特徴を正確に再現しています。

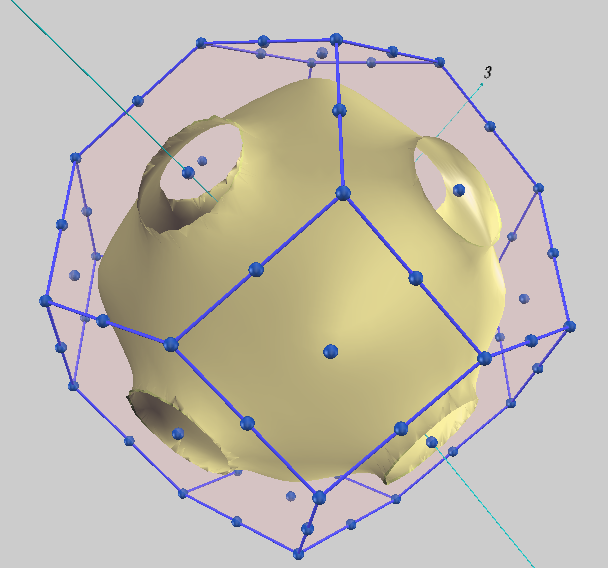
図2　銅 (Cu) のフェルミ面

2. マグネシウム (Mg) - バンドの重なりを持つ2価金属#

2価の金属であるマグネシウム（Mg）では、価電子帯（3sバンド）と伝導帯（3pバンド）のエネルギーが重なる「バンドオーバーラップ」が生じます。これにより、フェルミエネルギーは複数のバンドを横切ることになります。今回の計算では3本のバンドがフェルミエネルギーを横切り、その結果、フェルミ面は図3に示すように複数の「シート」から構成される複雑な形状となります。ブリルアンゾーン中央の「モンスター」と呼ばれる正孔シートと、上下に見える「レンズ」状の電子シートが共存しており、2価金属に典型的な電子構造が正しく計算されていることが確認できました。

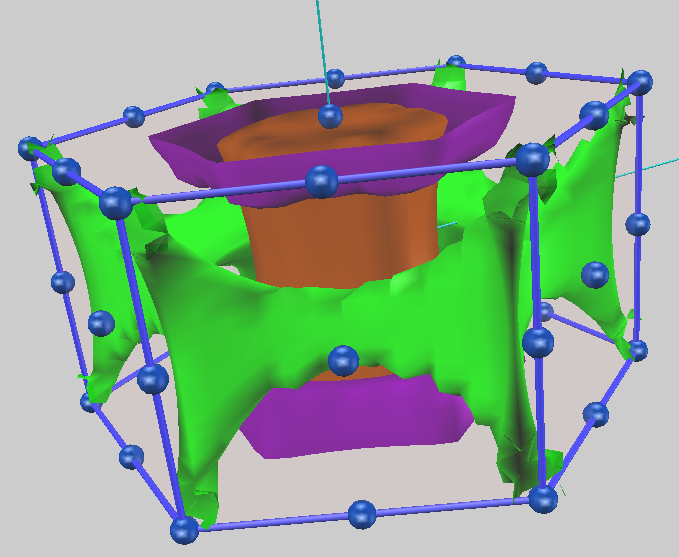
図3　マグネシウム (Mg) のフェルミ面

3. 鉄 (Fe) - 強磁性金属の電子状態#

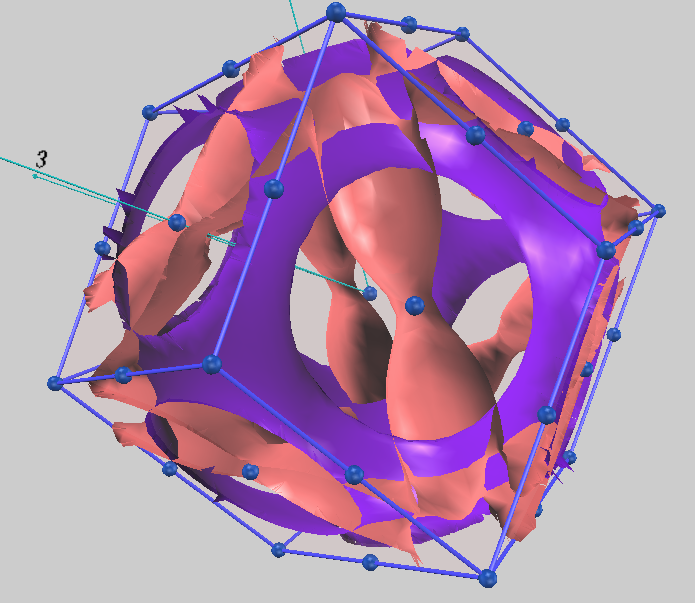
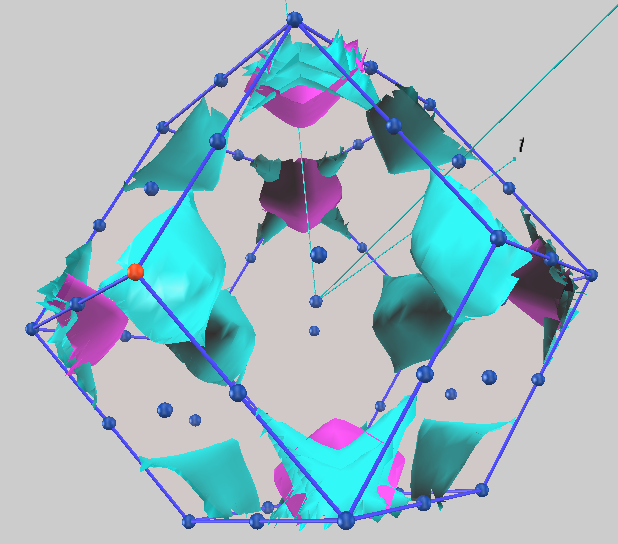
強磁性体である鉄（Fe）は、電子のスピンの向き（アップスピンとダウンスピン）によってエネルギー状態が大きく異なるという特徴を持ちます。この「交換分裂」により、アップスピン電子とダウンスピン電子のバンド構造は非対称になり、それぞれが異なる形状のフェルミ面を形成します。図4に示すように、アップスピンとダウンスピンのフェルミ面は全く異なる形状となりました。多数派であるアップスピンのフェルミ面は複雑に絡み合った大きな構造を持つのに対し、少数派のダウンスピンのフェルミ面は比較的小さな複数のシートからなります。この非対称性こそが鉄の磁性の源泉であり、本計算はスピン分極した系の電子状態を正確に記述できることを示しています。

鉄(Fe)のスピンアップのフェルミ面
図4(a) 鉄 (Fe) のスピンアップのフェルミ面
鉄(Fe)のスピンダウンのフェルミ面
図4(b) 鉄 (Fe) のスピンダウンのフェルミ面

まとめ#

第一原理計算ソフトウェアAdvance/PHASEを用いて、Cu、Mg、Feのフェルミ面を計算しました。その結果、Cuについては1価金属に典型的な単純な形状、Mgについてはバンドの重なりに起因する複雑なシート構造、そしてFeについては強磁性に由来するスピン分裂した非対称な電子状態がそれぞれ得られました。これらの結果は、既存の理論や実験で知られている各物質の物理的特徴と整合しております。

参考文献#

  1. N. W. Ashcroft and N. D. Mermin, Solid State Physics (Thomson Learning, 1976).

  2. G. A. Burdick, "Energy Band Structure of Copper," Phys. Rev. 129, 138 (1963).

  3. J. B. Ketterson and R. W. Stark, "Fermi Surface of Magnesium. I.Magnetoacoustic Attenuation," Phys. Rev. 156, 748 (1967).

  4. S. Wakoh and J. Yamashita, "Band Structure of Ferromagnetic Iron Self-Consistent Procedure," J. Phys. Soc. Jpn. 21, 1712 (1966).

関連ページ#