コンテンツにスキップ

高圧でのhcp Feの第一原理計算#

PHASE logo

地球の核内部のような超高圧環境下（～200GPa以上） における鉄（Fe）は、我々が常圧で目にする物理的状態とは大きく異なります。特に地球の内核に相当する超高圧領域では、鉄は六方最密充填構造（hcp構造）をとり、常圧の強磁性・体心立方晶(bcc)鉄とは異なり、非磁性（non-magnetic）状態であると考えられています。これらの極限環境下での物性（特に圧力-体積関係や結晶構造のc/a比）を正確に理解することは、地球物理学において極めて重要です。本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、超高圧下におけるhcp Feの構造とP-V特性を計算し、実験データとの詳細な比較を行います。

Keywords: 第一原理計算, 高圧物性, hcp Fe, 地球コア, 状態方程式 (EOS), P-V曲線, c/a比

計算モデルと計算条件#

本計算では、高圧相であるhcp Feの非磁性状態をモデル化しました (図1)。

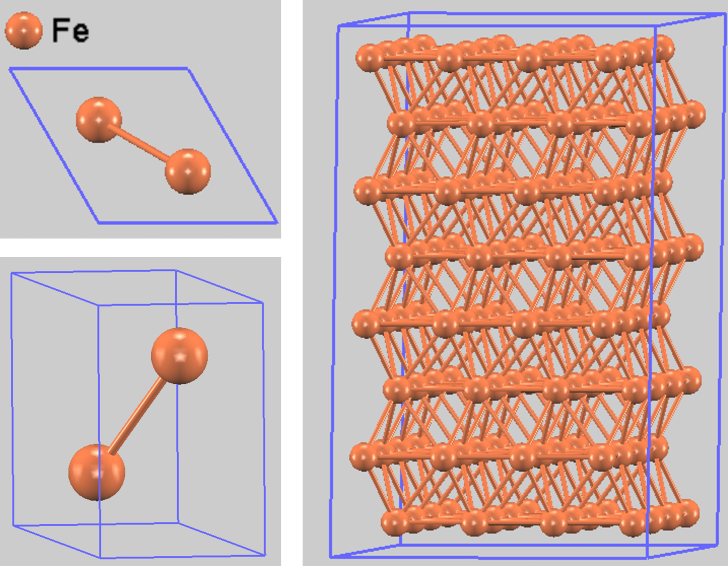
hcp Feの計算モデル

図1.　hcp Feの構造モデル。左上：計算セルの上面図、左下：計算セルの斜視図、右：視認性のための4x4x4スーパーセル表示。

高圧計算では、波動関数や電子密度が空間的に急峻に変化するため、計算パラメータには特に注意が必要です。本解析では、通常の計算よりも著しく高いカットオフエネルギーと、金属である鉄のブリルアンゾーン積分を正確に行うための密なk点メッシュを採用しました。

主な計算条件は表1に示されています。

表1.　主な計算条件

項目 設定
擬ポテンシャル PAWポテンシャル
交換相関汎関数 GGA (PBE)
波動関数のカットオフエネルギー 50 Rydberg
電荷密度のカットオフエネルギー 500 Rydberg
k点サンプリング 19x19x10

計算結果と考察#

E-V曲線と状態方程式#

まず、超高圧領域を含む、様々なセル体積（Volume）における系の総エネルギー（Energy）を計算し、E-V曲線を作成しました。この計算結果（青丸）をBirch-Murnaghan 状態方程式（EOS）を用いてフィッティング（オレンジ線）しました。

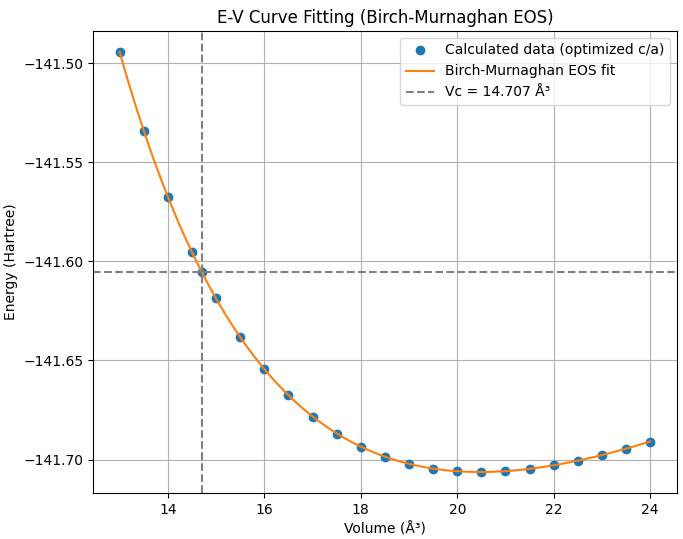
hcp FeのE-V曲線とBirch-Murnaghan EOSフィッティング

図2.　超高圧領域を含む、hcp FeのE-V曲線とBirch-Murnaghan EOSフィッティング。

実験論文 [1]で報告されている地球コア内部に相当する密度 = 12.61 g/cm3 （圧力値：211 GPa）に着目し、これに対応する体積 = 14.707 Å3 を特定しました。この体積は、図2のE-V曲線の極小値（平衡体積）よりもかなり小さい、強い圧縮状態にあることを示しています。

最適c/a比の計算と実験比較#

次に、この高圧下の体積 Vc = 14.707 Å3 を固定したまま、hcp構造のc/a比を様々に変化させてエネルギー計算を行いました。

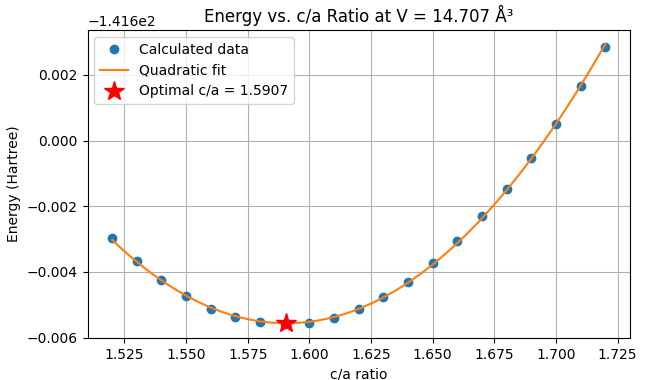
V = 14.707 Å3 におけるエネルギーとc/a比の関係

図3.　V = 14.707 Å3 におけるエネルギーとc/a比の関係。放物線フィッティング（オレンジ線）により、エネルギーが最小となる最適c/a比が 1.5907（赤星）であることが決定されました。

この計算結果 1.5907 を、論文 [2] の実験データと比較しました。

  • 実験データ点との比較: 論文 [2] には、本計算の密度 (12.61 g/cm3) に非常に近い密度 12.64 g/cm3 (圧力 212.1 GPa) でのc/a比が 1.596 と報告されています。
  • 実験の近似式との比較: 論文 [2] では、c/a比の圧力依存性が c/a = 1.604 - 4.9 x 10-5 * P (GPa) という線形近似式で示されています。実験圧力 211 GPa を代入すると、c/a比は 約1.594 と計算されます。

表2にこれらの値をまとめます。本計算によるc/a比 (1.5907) は、実験データ点 (1.596) および実験の近似式から得られる値 (約1.594) と良好な一致を示しています。

表2.　c/a比の比較 (V ≈ 14.7 Å3)

項目 c/a比
本計算値 (PBE) 1.5907
実験データ点 1.596
実験の近似式 (P=211 GPa) 約1.594

P-V曲線と圧力の比較#

最後に、E-V曲線の傾き () から計算される理論的なP-V曲線（0 K）と文献 [2] の実験データを比較しました。

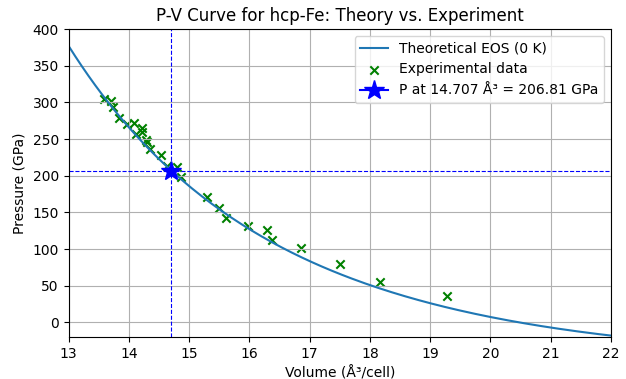
hcp FeのP-V曲線：理論と実験の比較

図4.　hcp FeのP-V曲線：理論 (青線) と実験データ (緑x) の比較。理論計算から Vc = 14.707 Å3 での圧力は 206.81 GPa (青星) と計算されました。

図4に示す通り、計算された状態方程式（青線）は、広範な圧力領域で実験データ（緑x）と非常によく一致しています。特に、我々が着目した体積 Vc = 14.707 Å3 における計算圧力は 206.81 GPa であり、実験値である 211 GPa との差はわずか2%程度と、高い精度で一致しています。

このような実験値との良好な一致は、本解析と同様の第一原理計算（LAPW法、GGA）を用いた他の理論研究 [3] においても、文献 [2] の実験データと比較検証されており 、超高圧下での鉄の物性を予測する上で第一原理計算が信頼性の高い手法であることが裏付けられています。

まとめ#

本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、地球コア内部に相当する超高圧環境下でのhcp Feの物性計算を行いました。高圧計算に要求される厳しい計算パラメータ（高いカットオフエネルギーと密なk点メッシュ） を適用することで、hcp Feのc/a比 およびP-V状態方程式を高い精度で算出しました。計算されたc/a比 (1.5907) や圧力 (206.81 GPa) は、報告されている実験値 (c/a ≈ 1.594-1.596, P = 211 GPa) と良好な一致を示しました。これは第一原理計算が、こうした極限環境下における材料の物性を正確に予測・解明するための強力なツールであることを示しています。

参考文献#

  1. H. K. Mao, J. Shu, G. Shen, R. J. Hemley, B. Li, and A. K. Singh, "Elasticity and rheology of iron above 220 GPa and the nature of the Earth's inner core", Nature 396, 741 (1998).
  2. H. K. Mao, Y. Wu, L. C. Chen, J. F. Shu, and A. P. Jephcoat, "Static compression of iron to 300 GPa and Fe0. 8Ni0. 2 alloy to 260 GPa: Implications for composition of the core", Journal of Geophysical Research: Solid Earth 95, 21737 (1990).
  3. L. Stixrude, E. Wasserman, and R. E. Cohen, "Composition and temperature of Earth's inner core", Journal of Geophysical Research: Solid Earth 102, 24729 (1997).

関連ページ#