磁気消失を伴う鉄の圧力誘起相転移シミュレーション#

鉄(Fe)は、常温常圧では強磁性を示す体心立方格子(bcc)構造をとりますが、高圧下では磁性を失い、六方最密充填(hcp)構造へと相転移します。この現象は、地球中心核のような極限環境下での物質の状態を理解する上で極めて重要です。本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、鉄の圧力誘起相転移をシミュレーションしました。エネルギーと体積の関係から状態方程式を求め、2つの異なる手法を用いて相転移圧力を算出することで、第一原理計算による物性予測の精度と有効性を検証します。
Keywords: 第一原理計算, DFTシミュレーション, 鉄, 相転移, 高圧, 状態方程式, 共通接線法, bcc, hcp
計算モデルと計算条件#
本解析では、鉄の低圧相であるbcc構造と高圧相であるhcp構造の2つの結晶構造をモデル化しました(図1)。それぞれの構造について、体積を様々に変化させながら第一原理計算を行い、エネルギーが最も低くなる安定な状態を求めました。
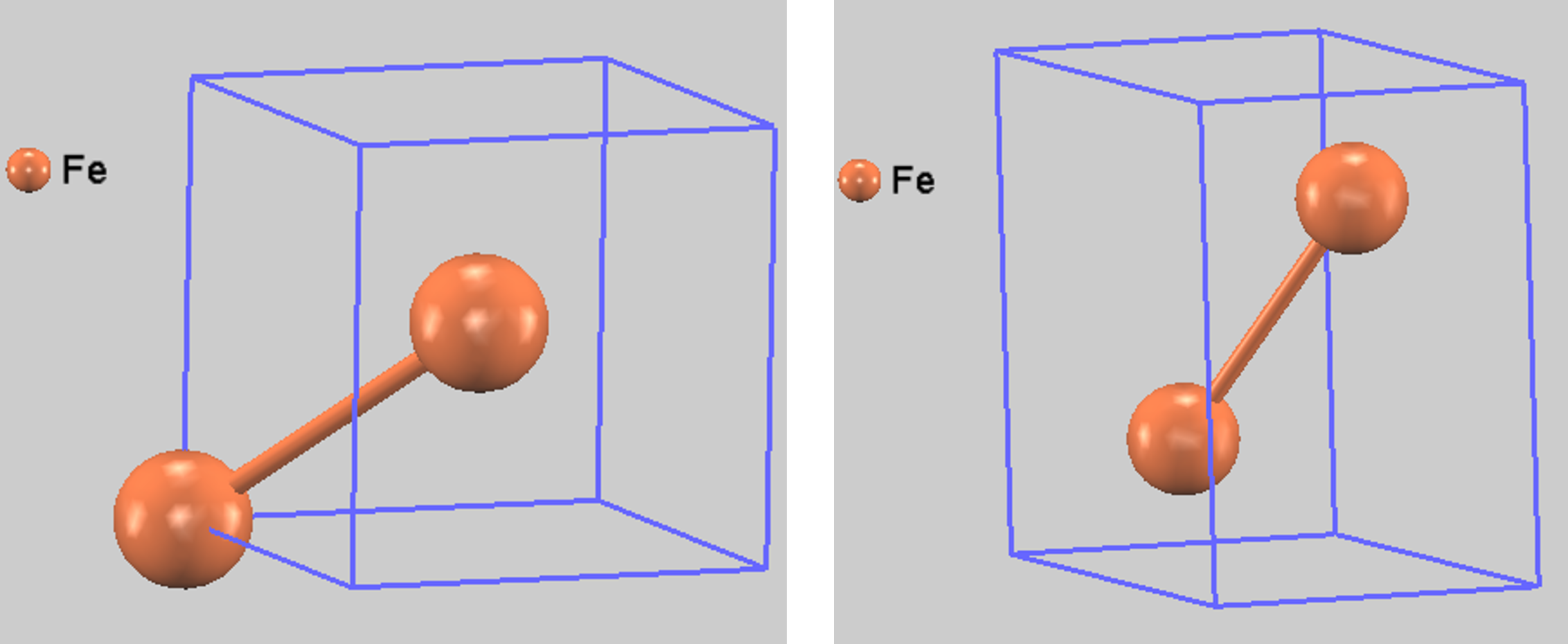
図1. (左) bcc構造モデル (右) hcp構造モデル
表1. 計算条件の概要
| 項目 | 設定 |
|---|---|
| 擬ポテンシャル | PAWポテンシャル |
| 交換相関汎関数 | GGA (PBE) |
| カットオフエネルギー | 25 Rydberg (約340 eV) |
| k点サンプリング | 11x11x11 (bcc), 13x13x8 (hcp) |
| 初期スピン分極 | 0.275 |
計算結果と考察#
bcc相(低圧相)の計算結果#
bcc構造について、体積を変化させた際の全エネルギーをプロットし、E-V曲線(状態方程式)を作成しました(図2)。曲線が最も低くなる点が、その物質が最も安定して存在する状態(平衡状態)を示します。この計算から、bcc鉄の平衡体積は23.00 Å3、原子あたりは11.50 Å3と求められました。
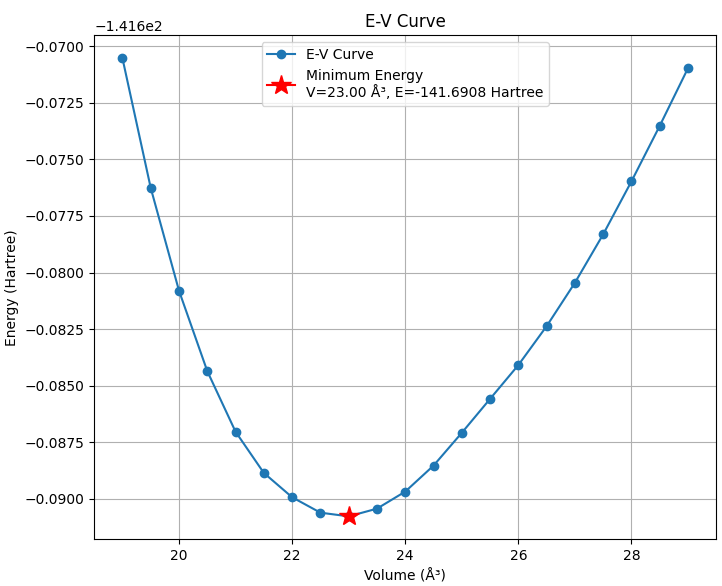
図2. bcc構造のE-V曲線。エネルギー最低点(赤星)が平衡状態に対応します。縦軸の値に対して、-1.416e2 (つまり、-141.6)というオフセットが軸の上端が示されています。
また、各体積における磁気モーメントを計算したところ、bcc鉄は強磁性を示すことが確認されました(図3)。磁気モーメントの大きさは体積に依存し、体積が小さくなる(圧力が高くなる)ほど減少する傾向が見られます。
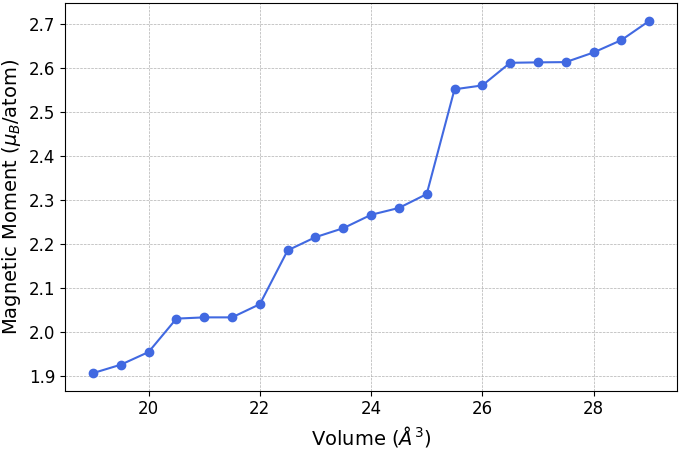
図3. bcc構造における磁気モーメントと体積の関係。
hcp相(高圧相)の計算結果#
hcp構造では、体積だけでなく格子定数の比(c/a比)もエネルギーに影響します。そのため、様々な体積とc/a比でエネルギーを計算し、E-V-c/a曲面を作成しました(図4)。各体積でエネルギーが最小となるようにc/a比を最適化し、得られたデータからhcp相のE-V曲線を求めました(図5)。
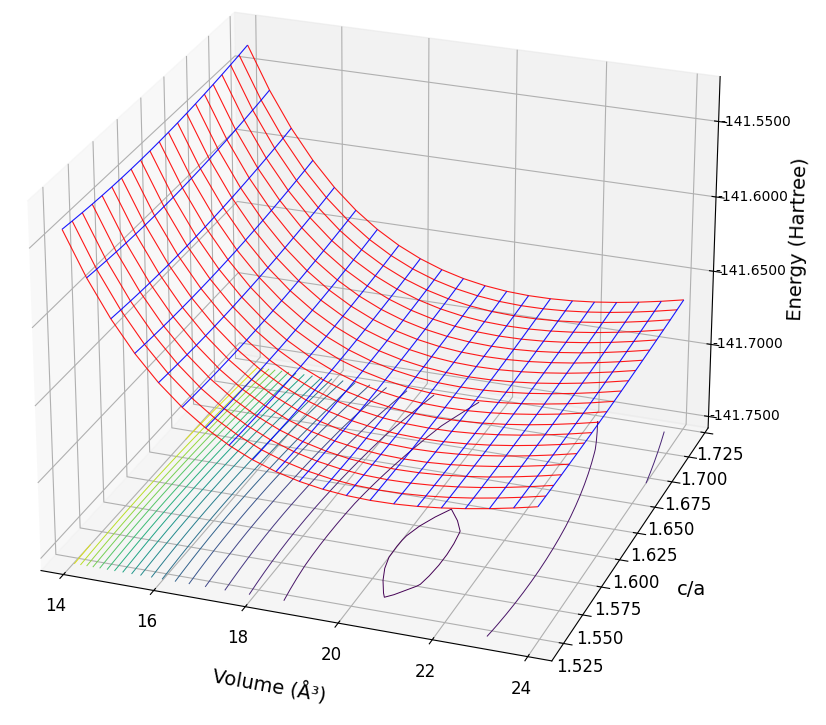
図4. hcp構造のE-V-c/a曲面
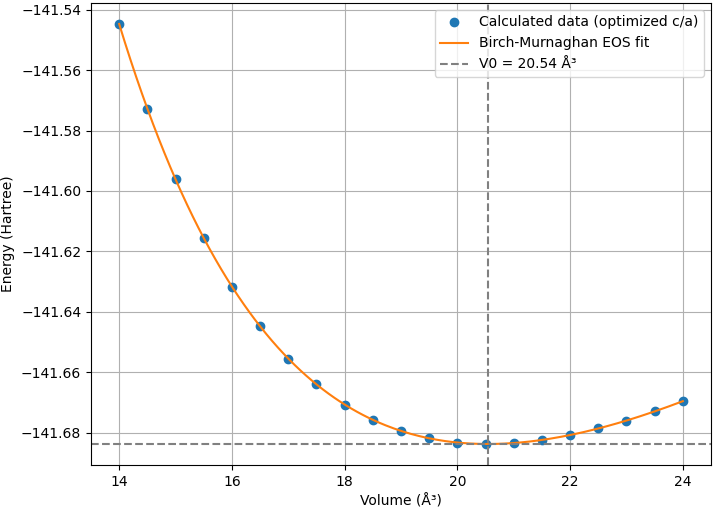
図5. 最適化されたc/a比を持つhcp構造のE-V曲線
hcp構造の計算結果から、磁気モーメントは0.00 μBとなり、高圧下では鉄の磁性が消失することが理論的に再現されました。E-V曲線のフィッティングから得られた物性を表2にまとめます。
表2. hcp構造の計算物性値
| 項目 | 計算値 |
|---|---|
| 平衡格子定数 a0 | 2.4681 Å |
| 平衡格子定数 c0 | 3.8934 Å |
| c/a 比 | 1.5775 |
| 平衡体積 V0 | 20.5386 Å3 |
相転移圧力の算出#
bcc相からhcp相へ転移する圧力は、両相のギブスの自由エネルギー G (= E + PV) が等しくなる点として定義されます。ここでは、E-V曲線を用いて転移圧力を算出する代表的な2つの手法を紹介します。
方法1: 共通接線法#
共通接線法は、2つの相のE-V曲線に同時に接する直線(共通接線)を引くことで転移圧力を求めるグラフィカルな手法です。転移点では、両相の圧力 が等しく、ギブス自由エネルギーも等しくなります。共通接線の傾きが転移圧力(の符号を反転させたもの)を与え、その切片がギブス自由エネルギーに対応します。図6に示すように、bcc相とhcp相のE-V曲線に共通接線を引くことで、転移圧力を求めました。
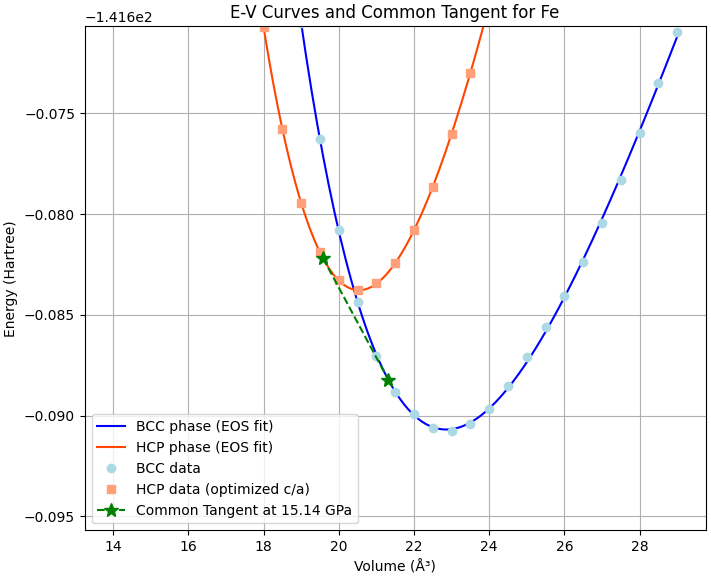
図6. 共通接線法による転移圧力の算出。計算された転移圧力は15.14 GPaです。
方法2: P-V曲線による算出(マクスウェル構成)#
この方法では、まずE-V曲線を体積で微分して、各相のP-V曲線()を求めます。相転移は両相のギブス自由エネルギー が等しくなる圧力点で生じますが、この条件はP-V曲線を用いてより直感的に理解できます。
圧力Pにおけるギブス自由エネルギーは、ゼロ圧力でのエネルギー(E0)と圧力による変化量()の和で表されます。転移圧力 では となるため、以下の関係が成り立ちます。 この式を整理すると、転移圧力は次の条件を満たす圧力であるとわかります。 つまり、「2つの相のゼロ圧力におけるエネルギー差(左辺)が、P-V線図上で2つの曲線に挟まれた面積(右辺)と等しくなる」圧力こそが、求める転移圧力です。図7の灰色で示された面積はまさにこの積分値を表しており、この面積がゼロ圧力でのエネルギー差と等しくなる圧力として、転移圧力を15.14 GPaと決定しました。この結果は共通接線法とも完全に一致します。
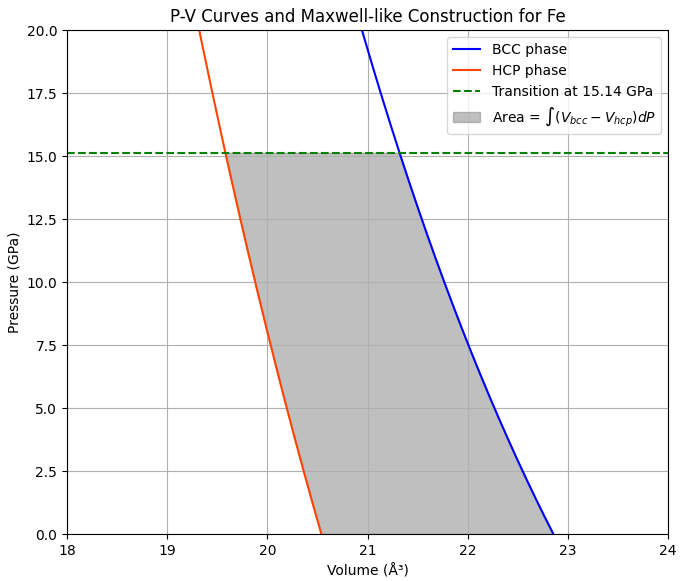
図7. P-V曲線とマクスウェル構成による転移圧力の算出。灰色部分の面積は、横軸の体積Vを被積分関数、縦軸の圧力Pを積分範囲(0から転移圧力まで)として算出した値であり、これが両相のエネルギー差に等しくなる圧力を求めます。
実験やほかの計算との比較#
本計算で得られた相転移圧力15.14 GPaは、実験値(約13 GPa)[1, 2] と良好な一致を示しています。また、構造物性(平衡体積、平衡格子定数)については、FP-LAPWを用いた計算 [3] の結果とほぼ一致しますが、相転移圧力には数GPaの差異が見られます。この圧力の差は、計算条件の違いに起因するものと考えられます。
まとめ#
本解析では、第一原理計算ソフトウェアAdvance/PHASEを用いて、鉄の圧力誘起によるbcc-hcp相転移をシミュレーションしました。常圧での強磁性bcc相と高圧での非磁性hcp相の電子状態と構造を正確に再現し、両相の状態方程式を求めました。共通接線法とP-V曲線法の2つの手法を用いて算出した相転移圧力は、いずれも15.14 GPaとなり、手法間で高い整合性を示しました。この計算値は実験値とも良好な一致を示しており、第一原理計算が複雑な相転移現象を解明し、物質の物性を高精度に予測するための強力なツールであることを実証しました。
本解析の詳細や、研究への適用可能性に関するご相談はこちら
お問い合わせ参考文献#
- D. Bancroft, E. L. Peterson, and S. Minshall, "Polymorphism of iron at high pressure", J. Appl. Phys. 27, 291(1956).
- F. M. Wang, and R. Ingalls, "Iron bcc-hcp transition: Local structure from x-ray-absorption fine structure", Phys. Rev. B 57, 5647 (1998).
- M. Ekman, B. Sadigh, K. Einarsdotter, and P. Blaha, "Ab initio study of the martensitic bcc-hcp transformation in iron", Phys. Rev. B, 58, 5296 (1998).
関連ページ#
- 第一原理計算ソフトウェア Advance/PHASE
- 解析分野:ナノ・バイオ
- 産業分野:材料・化学