六方晶の構造物性評価：E-V曲線とc/a比最適化によるアプローチ#

PHASE logo

六方晶（HCP）構造は多様な材料でみられる基本的な結晶構造の一つです。その物性は結晶の軸比（c/a比）に大きく依存しますが、このc/a比は理想的な最密充填構造の値（約1.633）からずれることが少なくありません。したがって、材料の真の安定構造と物性を正確に予測するためには、体積とc/a比の両方を同時に最適化するアプローチが不可欠です。この最適化におけるエネルギー曲面を解析することで、平衡格子定数や体積弾性率といった重要な物性値を、一度の系統的な計算から高精度に導き出すことが可能になります。本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、金属、硬質材料、機能性セラミックスなど、多様なHCP材料を例として、この手法の汎用性と有効性を示します。

Keywords: 第一原理計算, E-V曲線, c/a比, 格子定数, 体積弾性率, 六方晶, HCP

計算手法#

六方晶構造の安定構造と物性値を精密に決定するため、単に体積を変化させるだけでなく、体積とc/a比を同時に最適化する必要があります。本解析では、各体積でc/a比と原子座標を最適化し、得られた計算結果を状態方程式でフィッティングするという手法を用います。この手法では、物理的意味に基づいた信頼性の高い2段階のフィッティングを以下の通り行います。

ステップ1：各体積における最適c/a比の決定#

まず、複数の体積点を固定しそれぞれの体積においてc/a比を様々に変化させた全エネルギー計算（第一原理計算）で得られた(c/a, エネルギー)のデータセットをフィッティングします。エネルギーが極小となるc/a比近傍は放物線（2次関数）でよく近似できるため、2次関数フィッティングを適用します。

このフィッティングにより、各体積 $V$ におけるエネルギー $E$ が最小となる最適c/a比と、その時の最小エネルギー $E_\text{min}$ を高精度に決定します。この操作を計算した全ての体積点について行います。

ステップ2：状態方程式（EOS）による物性値の導出#

次に、ステップ1で得られた (V, E_min) の組からなる、より信頼性の高いE-V曲線を作成します。このE-V曲線を、以下の3次のバーチ・マーナハンの状態方程式（3rd-order Birch-Murnaghan EOS）にフィッティングします [1]。

$E(V) = E_0 + \frac{9 V_0 B_0}{16} \left\{ \left[ \left( \frac{V_0}{V} \right)^{\frac{2}{3}} - 1 \right]^3 B'_0 + \left[ \left( \frac{V_0}{V} \right)^{\frac{2}{3}} - 1 \right]^2 \left[ 6 - 4 \left( \frac{V_0}{V} \right)^{\frac{2}{3}} \right] \right\}$

このフィッティングにより、平衡体積 $V_0$ 、体積弾性率 $B_0$ 、およびその圧力微分 $B'_0$ といった重要な物性値が算出されます。最終的に、得られた $V_0$ と、対応する最適c/a比 $(c/a)_0$ （補間法などにより算出）を用いて、平衡格子定数 $a_0$ と $c_0$ が一意に定まります。

この一連の2段階フィッティングプロセスは、Advance/PHASEに同梱されているPython環境を利用することで、単一のPythonスクリプトとして完全に自動化することが可能です。これにより、第一原理計算の出力データから最終的な物性値の算出までを効率的実行できます。

計算結果と考察#

本手法の有効性と汎用性を実証するため、異なる特性を持つ5つの六方晶（HCP）物質の解析を行いました。

事例1: コバルト (Co, HCP) - 典型的な磁性金属#

六方最密充填（HCP）構造を持つ代表的な磁性金属、コバルト（Co）の解析を行いました。計算条件はカットオフエネルギー25 Rydberg、k点サンプリングは10×10×6、Co原子の初期スピン分極値は0.4です。図1に3DのE-V曲線と、そこから得られた最適c/aにおけるE-V曲線のフィッティング結果を示します。

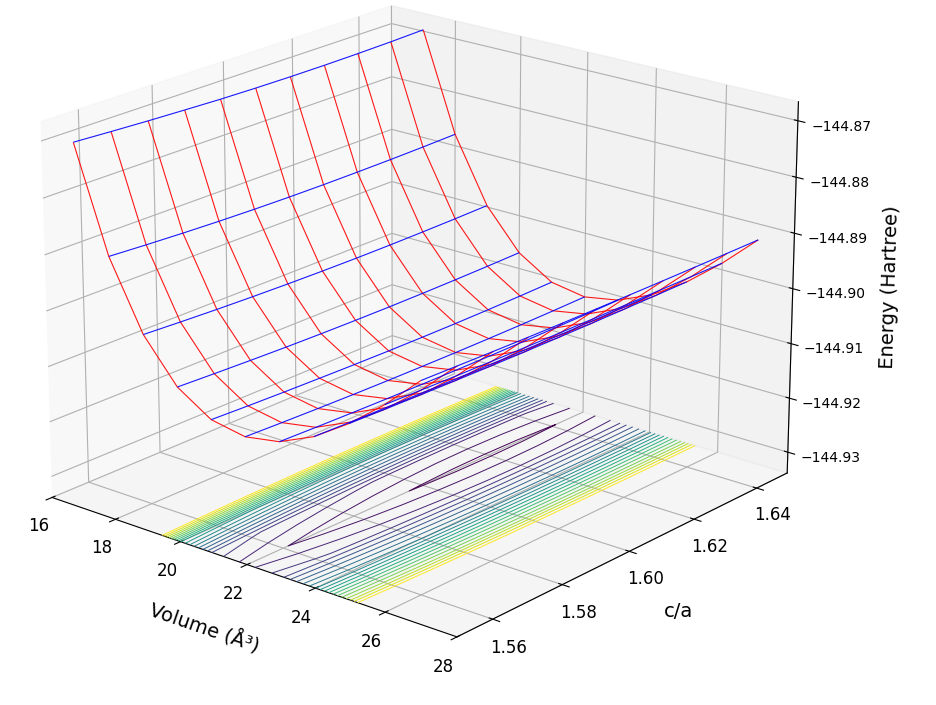
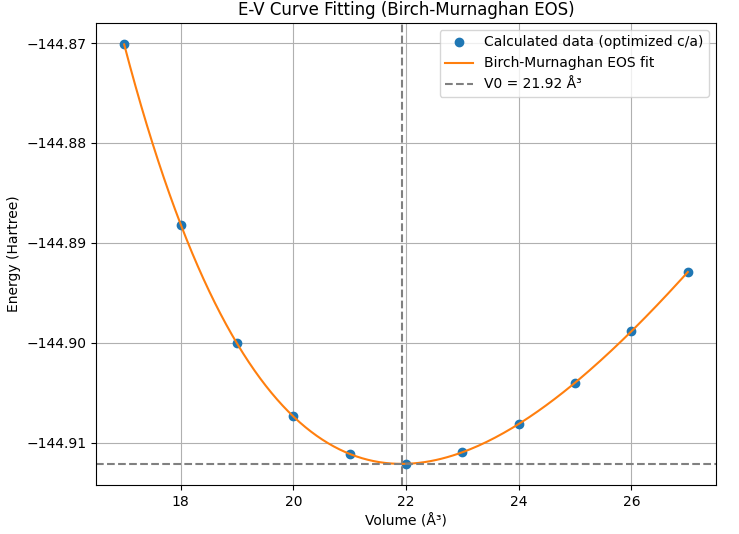
CoのEOSフィッティング
図1.　CoのE-V曲線（上）とBirch-Murnaghan EOSフィッティング（下）

計算で得られた格子定数a, cは、表1に示すように実測値との誤差がそれぞれ0.5%未満と非常に小さく、c/a比（1.618）も理想値（1.633）に近い実測値（1.62）をよく再現しています。体積弾性率（208.3 GPa）は、文献 [2] で報告されている実測値（203 GPa）よりわずかに大きく評価されていますが、良好な一致です。

表1.　Coの計算値と実測値の比較

	計算値	実測値
格子定数 a (Å)	2.50	2.51
格子定数 c (Å)	4.05	4.07
c/a	1.618	1.62
体積弾性率 (GPa)	208.3	203

事例2: ハフニウム (Hf, HCP) - Coとは異なる遷移金属#

優れた耐食性を持つ遷移金属、ハフニウム（Hf）を解析しました。計算条件はカットオフエネルギー25 Rydberg、k点サンプリングは8×8×6です。図2に3DのE-V曲線と、そこから得られた最適c/aにおけるE-V曲線のフィッティング結果を示します。

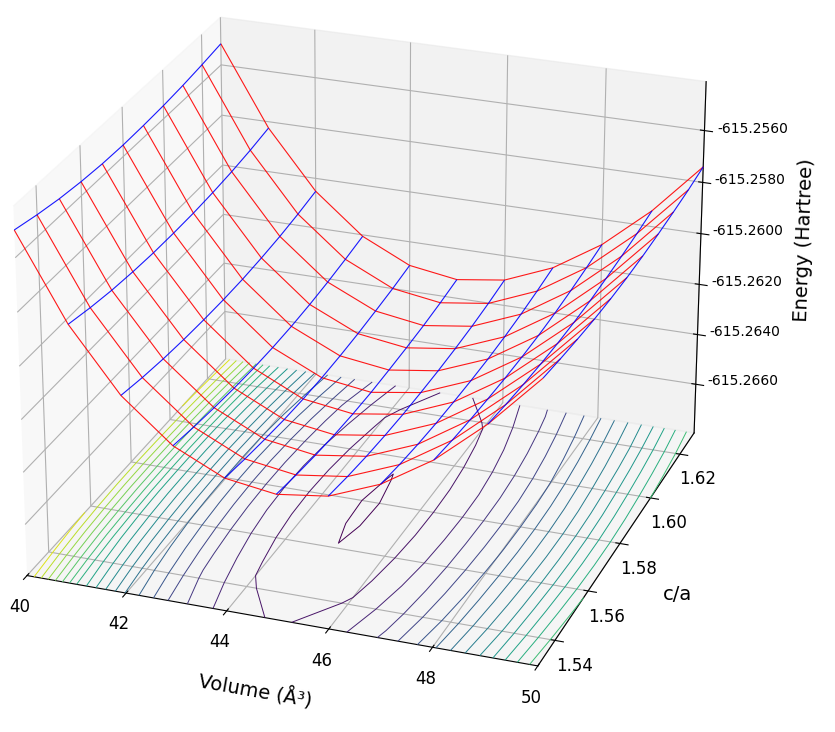
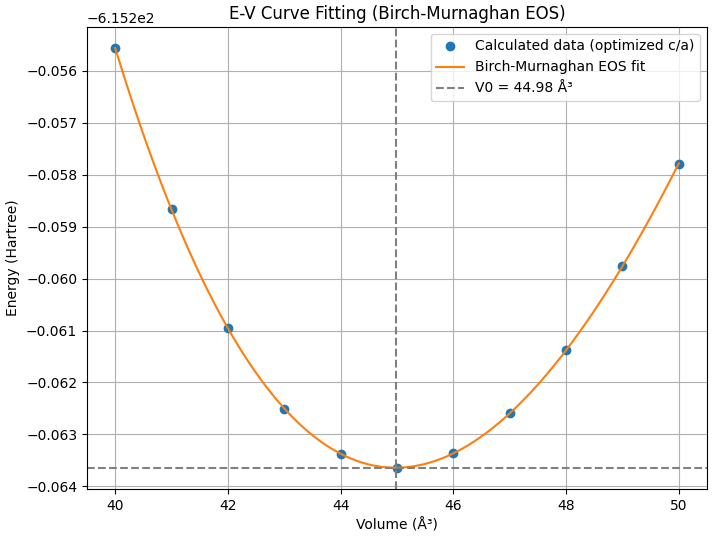
HfのEOSフィッティング
図2.　HfのE-V曲線（上）とBirch-Murnaghan EOSフィッティング（下）

Hfの計算結果も、表2に示す通り、格子定数とc/a比は実測値とよく一致しています。体積弾性率（107.1 GPa）は、文献 [3] で報告されている実験値（110 GPa）と良好な一致を示しました。

表2.　Hfの計算値と実測値の比較

	計算値	実測値
格子定数 a (Å)	3.203	3.19
格子定数 c (Å)	5.061	5.05
c/a	1.580	1.58
体積弾性率 (GPa)	107.1	110

事例3: 炭化タングステン (WC, HCP) - 特異なc/a比を持つ硬質材料#

超硬材料として知られる炭化タングステン（WC）を解析しました。WCはHCP構造ですが、c/a比が理想値から大きく外れる特徴があります。計算条件はカットオフエネルギー25 Rydberg、k点サンプリングは10×10×10です。図3に示すように、c/a比が1に近い領域でエネルギーが最も低くなることが分かります。

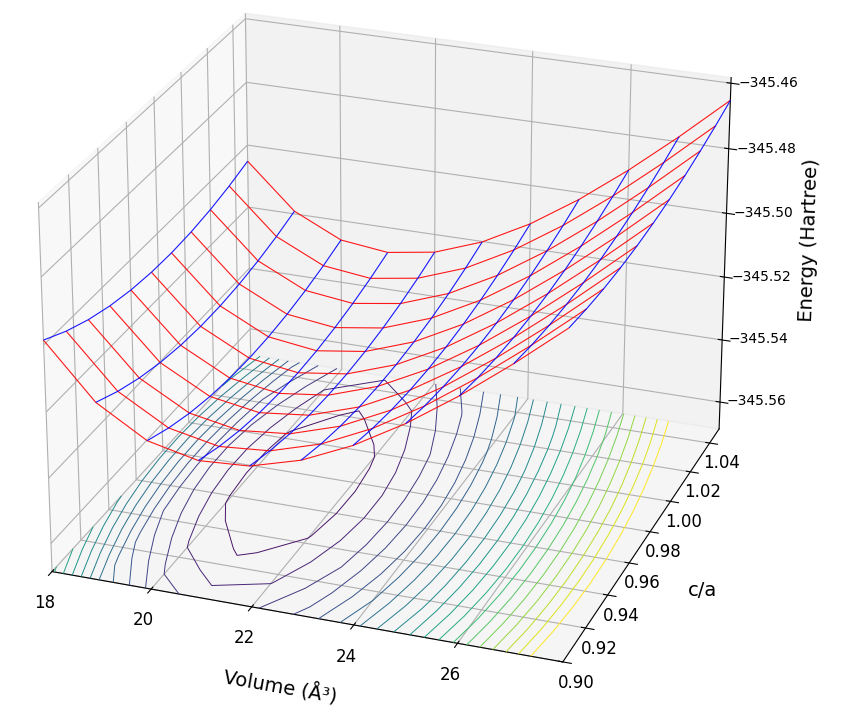
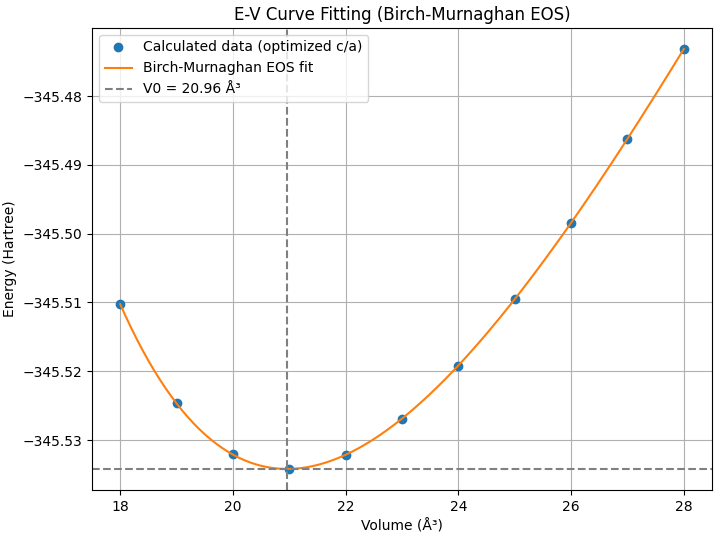
WCのEOSフィッティング
図3.　WCのE-V曲線（上）とBirch-Murnaghan EOSフィッティング（下）

表3に示す計算結果は、実測のc/a比（0.976）を0.977と非常によく再現しており、WCの特異な構造を理論的に捉えることに成功しています。c/a比が理想値(1.633)を大きく下回るこの構造が、W原子の平面とC原子の平面が交互に積層したものです。グラファイトのような層状物質とは異なり、W平面とC平面の間に強い結合が存在することが、WCの並外れた硬さの直接的な要因です。計算された体積弾性率（379.9 GPa）は、文献 [4] で報告されている実験値（384～412 GPa）に近い値であり、WCが超硬材料であることの理論的な裏付けとなります。

表3.　WCの計算値と実測値の比較

	計算値	実測値
格子定数 a (Å)	2.915	2.906
格子定数 c (Å)	2.848	2.837
c/a	0.977	0.976
体積弾性率 (GPa)	379.9	384～412

事例4: 酸化ベリリウム (BeO, HCP) - 機能性セラミックス#

高い熱伝導性と電気絶縁性を両立する機能性セラミックス、酸化ベリリウム（BeO）を解析しました。計算条件はカットオフエネルギー25 Rydberg、k点サンプリングは8×8×4です。解析結果を図4にまとめます。

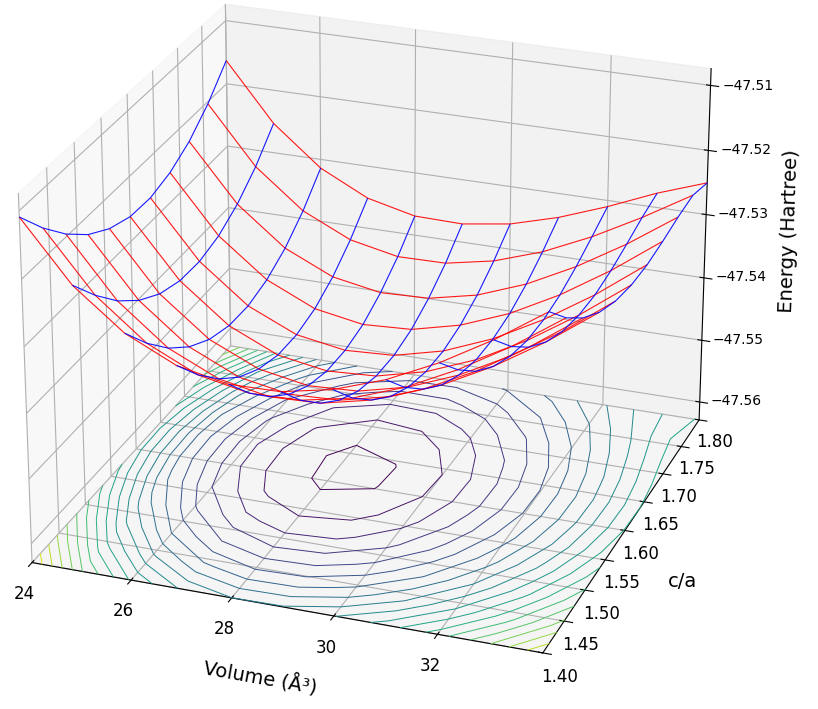
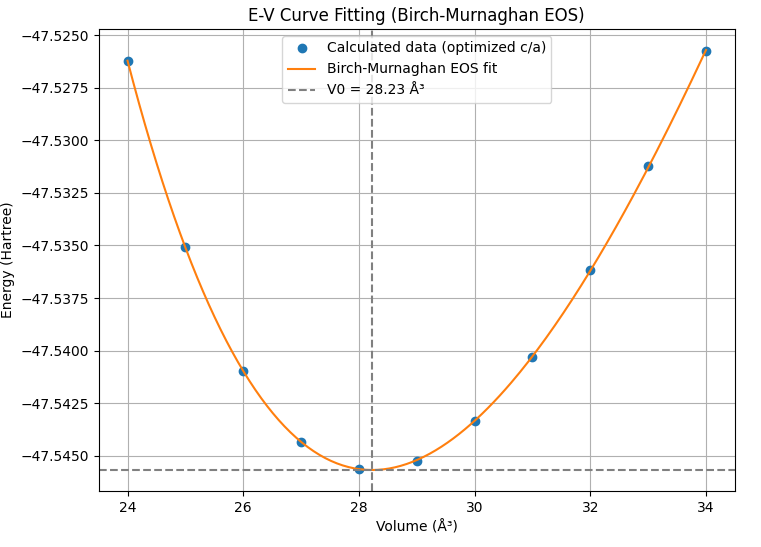
BeOのEOSフィッティング
図4.　BeOのE-V曲線（上）とBirch-Murnaghan EOSフィッティング（下）

表4の通り、BeOのc/a比は計算値で1.627と、理想値に非常に近い値を示しました。これはBeとOのイオン結合性が強いことを反映していると考えられます。体積弾性率の計算値（203.1 GPa）は実測値（210 GPa）[5] と近い値であり、構造パラメータの再現性は非常に良好です。

表4.　BeOの計算値と実測値の比較

	計算値	実測値
格子定数 a (Å)	2.716	2.699
格子定数 c (Å)	4.418	4.385
c/a	1.627	1.62
体積弾性率 (GPa)	203.1	210

事例5: 窒化アルミニウム (AlN, HCP) - ワイドギャップ半導体#

最後に、深紫外LEDなどの次世代半導体材料として注目される窒化アルミニウム（AlN）を解析しました。計算条件はカットオフエネルギー25 Rydberg、k点サンプリングは6×6×4です。図5に3DのE-V曲線と、そこから得られた最適c/aにおけるE-V曲線のフィッティング結果を示します。

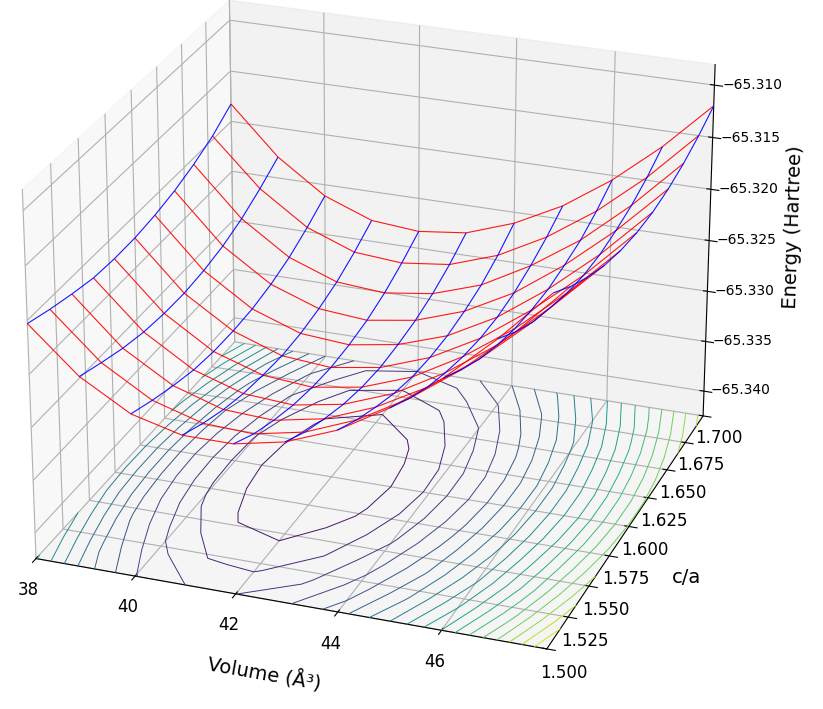
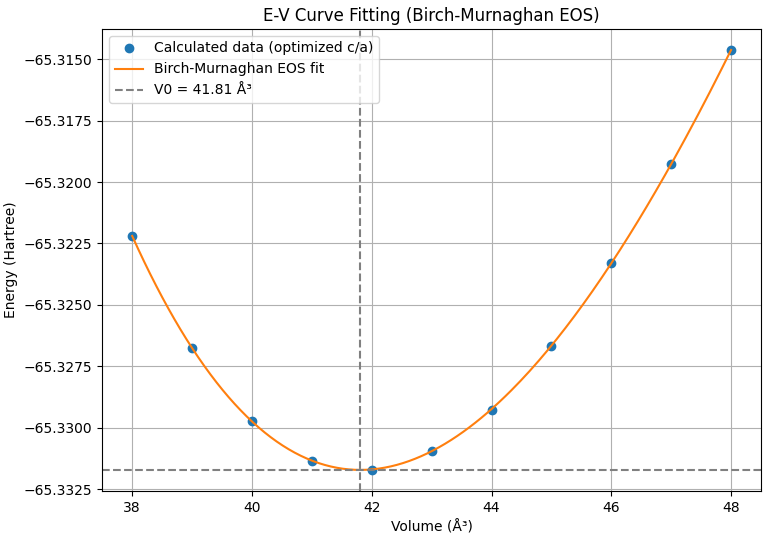
AlNのEOSフィッティング
図5.　AlNのE-V曲線（上）とBirch-Murnaghan EOSフィッティング（下）

表5に示すAlNの計算結果は、格子定数とc/a比において実測値と非常によく一致しています。また、体積弾性率（204.5 GPa）は、文献[6]で報告されている複数の実測値（200～203 GPa）とも整合しています。

表5.　AlNの計算値と実測値の比較

	計算値	実測値
格子定数 a (Å)	3.113	3.11
格子定数 c (Å)	4.980	4.98
c/a	1.599	1.60
体積弾性率 (GPa)	204.5	200, 201, 203

まとめ#

本解析では、第一原理計算ソフトウェアAdvance/PHASEと2段階フィッティング法を用い、金属（Co, Hf）、硬質材料（WC）、機能性セラミックス（BeO, AlN）という、多様な六方晶（HCP）材料の構造物性評価を行いました。いずれの事例においても、計算から得られた平衡格子定数、c/a比、体積弾性率は実測値と非常によく一致しました。特に、c/a比が理想値から大きく異なるWCの構造や、異なる結合タイプを持つ材料群の構造物性を高精度に再現できたことは、本手法の汎用性と信頼性の高さが示されています。

参考文献#

F. Birch, "Finite elastic strain of cubic crystals", Phys. Rev. 71, 809 (1947).
D. Antonangeli et al., "Anomalous pressure evolution of the axial ratio c/a in hcp cobalt: Interplay between structure, magnetism, and lattice dynamics", Appl. Phys. Lett., 92, 111911 (2008).
X. Qi, X. Wang, T. Chen, and B. Li, "Experimental and first-principles studies on the elastic properties of α-hafnium metal under pressure", J. Appl. Phys. 119, 125109 (2016).
B. L. Brugman et al., "Strength, deformation, and equation of state of tungsten carbide to 66 GPa", Acta Materialia 220, 117301 (2021).
R. M. Hazen and L. W. Finger, "High‐pressure and high‐temperature crystal chemistry of beryllium oxide", J. Appl. Phys. 59, 3728 (1986).
S. P. Dodd, G. A. Saunders, M. Cankurtaran, and B. James, "Ultrasonic study of the elastic and nonlinear acoustic properties of ceramic aluminum nitride", J. Mat. Sci. 36, 723 (2001).