コンテンツにスキップ

電極電位一定（Constant-μ）法による金属表面での分子吸着・拡散過程の第一原理計算#

走査トンネル顕微鏡（STM）観察や、二次電池、燃料電池といった電気化学デバイスの動作中など、多くの現実的な状況では、電極の電位は一定に保たれています。このような現象を理論計算で正確に再現するには、系の電子数を固定する従来の手法ではなく、系の化学ポテンシャル（電位）を一定に保ち、電子が自由に出入りできる「電位一定（Constant-μ）法」が有効です。本解析では、第一原理計算ソフトウェアAdvance/PHASEに実装されたConstant-μ法を用い、アルミニウム表面における分子の吸着構造や拡散過程が印加電圧によってどのように変化するかを、過剰電荷量の変化と共に示します。

Keywords: 第一原理計算, 電位一定, Constant-μ, FCP法, 有効遮蔽媒質(ESM)法, 構造最適化, NEB法, 拡散障壁, アルミニウム, 水分子, 過剰電荷

理論的背景： Constant-μ法#

Constant-μ法は、系の化学ポテンシャルμを目標値μtgtに保つ計算手法です。印加するバイアス電圧Uは、帯電していない中性状態の化学ポテンシャルμ0（PZC: Potential of Zero Charge）を基準として、次式で定義されます。

U = μtgt - μ0

Advance/PHASEでは、この手法をFictitiously Charged Particle (FCP)法 [1] として実装しています。FCP法では、系の過剰電荷量neを原子座標と同様の最適化自由度として扱い、電荷量に働く「仮想的な力」Fneを定義します。

Fne = μ - μtgt

原子に働く力がゼロになる点を探索して安定構造を決定するのと同様に、この「仮想的な力」がゼロになるよう（すなわち、系の化学ポテンシャルが目標値と一致するよう）過剰電荷量を最適化します。これにより、指定した電圧下での安定構造や反応経路を決定できます。この計算には、帯電したスラブモデルを扱うための有効遮蔽媒質（ESM）法 [2] が用いられ、特に真空／スラブ／金属（電極）という境界条件（model=3）が適用されます。

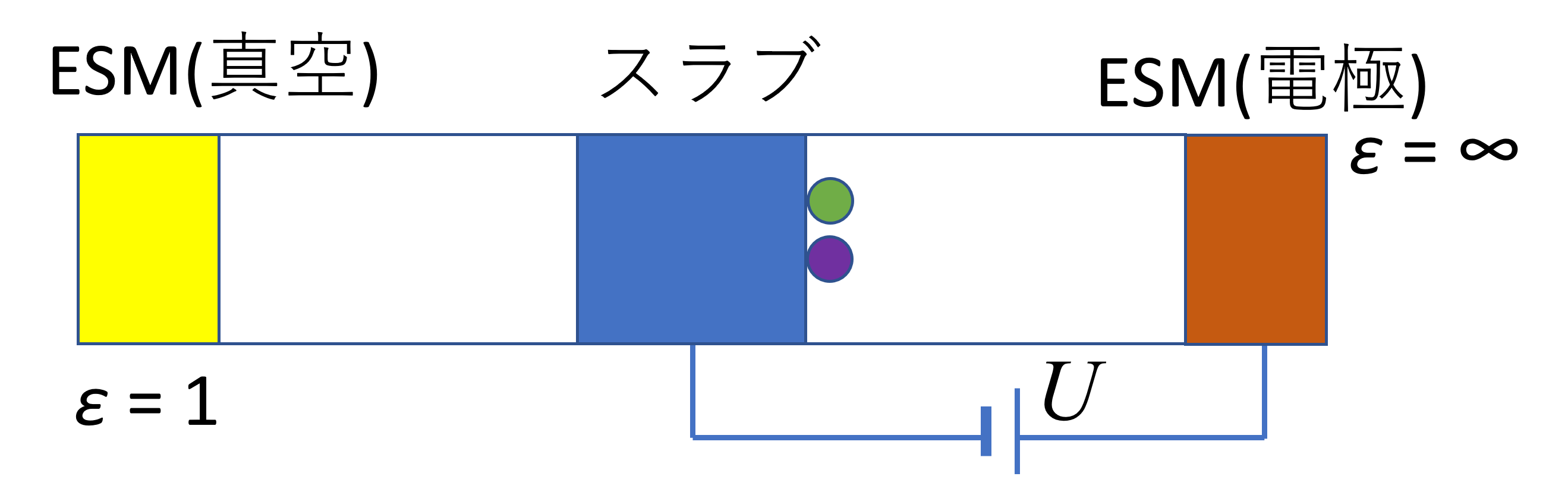
図1. 電圧を印加した際のESMモデル（真空／スラブ／電極）の概念図。スラブ（計算対象）は作用電極に相当し、右側のESM（金属）が対極として機能します。

解析事例1： Al(111)表面における水分子の電圧印加時の構造最適化#

計算モデルと計算条件#

Al(111)表面に吸着した一個の水分子（H₂O）の構造が、印加電圧によってどのように変化するかを調べました。計算モデルとして、5層のAl原子からなるp(2x2)スラブモデルを用い、下部の3層は固定しました。

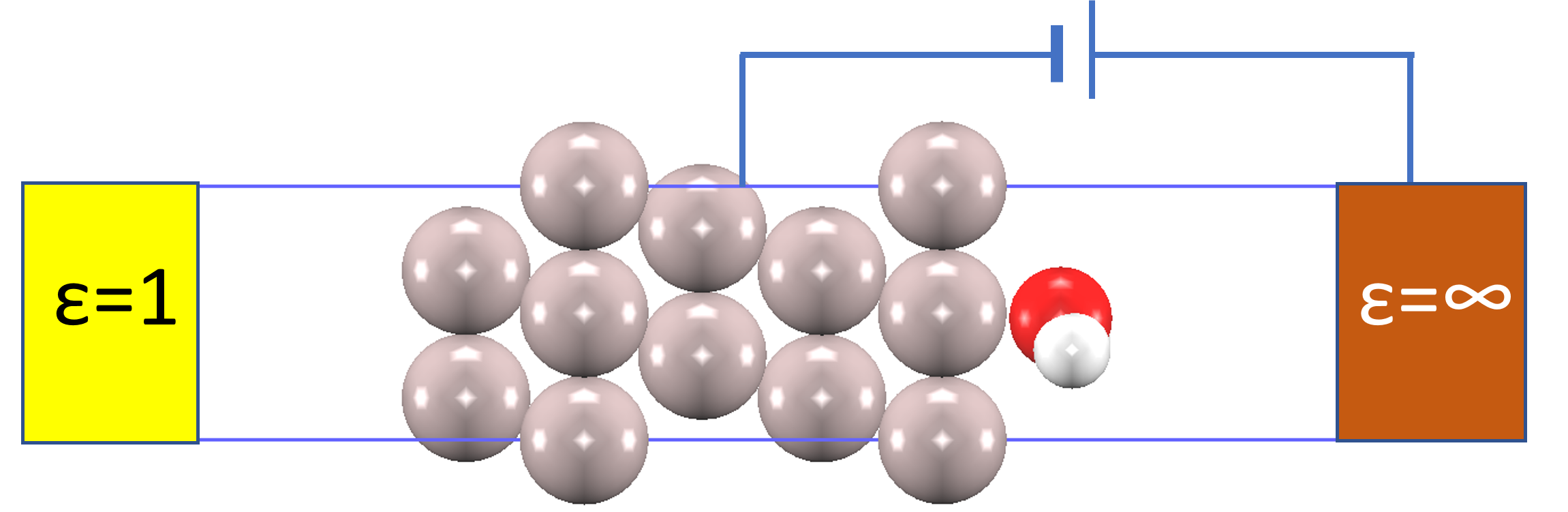
図2. Al(111)/H₂O系の計算モデル（側面図）。

主な計算条件を表1にまとめます。

表1. 計算条件の概要

項目 設定
擬ポテンシャル ウルトラソフト・ノルム保存擬ポテンシャル
交換相関汎関数 GGA (PBE)
波動関数のカットオフエネルギー 25 Rydberg
境界条件 ESM法 (model = 3)
k点サンプリング 5x5x1

計算結果と考察#

電圧を-1.0 Vおよび+1.0 V印加した際の構造最適化を行いました。印加電圧の正負にかかわらず、水分子のO原子はAl原子の真上（トップサイト）付近に吸着しましたが、分子の配向（傾き）は顕著に変化しました（図3）。

  • 負電圧印加時（-1.0 V）: スラブ表面が負に帯電します。これにより、水分子の正に分極している水素原子側が表面に引き寄せられ、分子はより水平に近い角度で吸着します。
  • 正電圧印加時（+1.0 V）: スラブ表面が正に帯電します。これにより、負に分極している酸素原子側が強く引きつけられ、水分子は表面に対してより垂直に近い角度で吸着します。

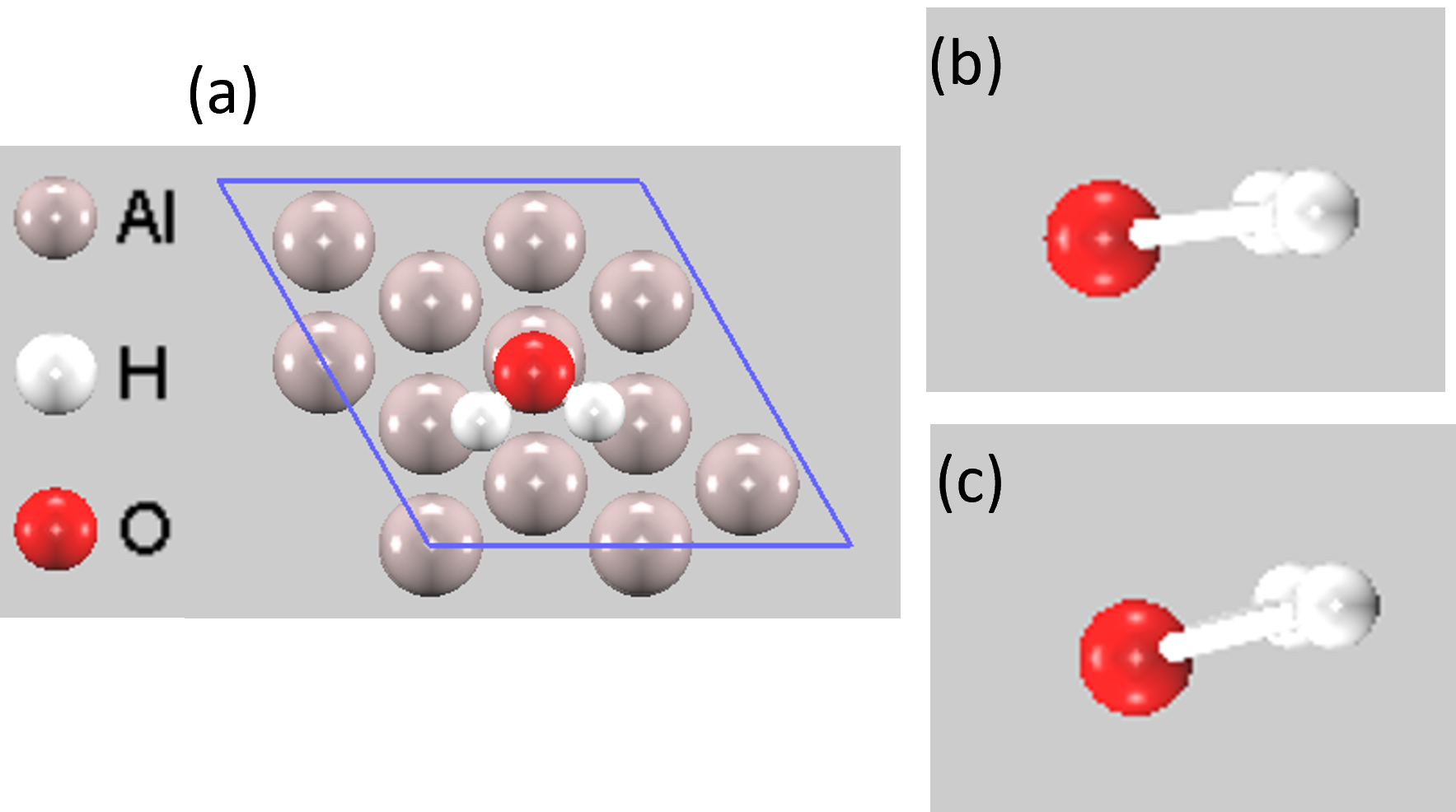
図3. (a) Al(111)表面に吸着した水分子の上面図。 (b) U = -1.0 V、(c) U = +1.0 V を印加した際のH₂Oの最適化構造。印加電圧によって水分子の傾きが変化していることがわかります。

Constant-μ計算の出力では、現在のフェルミエネルギー（Current EFermi）が目標値（Target EFermi）に近づき、FCPに働く力（Force acting on FCP）が収束基準 (この例では5.0x10⁻⁴ a.u.)を下回る様子が確認できます（出力例1）。

ID forcmx =   0.948850242882D-05
!FCP> Excess charge =  -0.2010838536868359E-01
!FCP> Current EFermi =  -0.171071918951802E+00 ( Target EFermi =  -0.171461062491367E+00 )
!FCP> Force acting on FCP =   -0.000389a.u.

出力例1. 構造最適化計算におけるFCP関連の出力。電荷量の最適化が収束基準を満たしたことを示しています。

解析事例2： Al(001)表面における水素原子の定電位拡散過程（NEB計算）#

計算モデルと計算条件#

次に、NEB（Nudged Elastic Band）法とConstant-μ法を組み合わせ、Al(001)表面での水素原子の拡散過程を解析しました。隣接するブリッジサイト間の拡散経路を、9個のイメージ（中間状態）を用いて計算しました。本計算は手法の有効性を実証するためのモデル計算であり、計算コストを考慮して、固定した単層のAl(001) p(2x2)スラブにH原子1個を吸着させた単純な系を採用しました。実際の定量的な議論には、スラブの層数を増やす、固定層を減らすなどのより精密なモデルが必要です。

計算結果と考察#

図4は、U = +1.0 Vの定電圧条件下で計算された水素原子の拡散経路を示しています。始状態から終状態まで各イメージでのH原子の位置を同じ図で表示されています。本計算はbridgeサイトからtopサイトを経由してbridgeサイトへの拡散経路を対象としています。

図4. (a) Al(001)表面での水素原子の拡散経路の模式図。 (b) U = +1.0 VにおけるH原子の拡散経路（NEB計算結果）。

電圧による拡散エネルギーの変化#

印加する電圧を変えて拡散エネルギー障壁を計算した結果を図5に示します。正の電圧を印加すると活性化エネルギーが低下し、負の電圧では上昇することが確認されました。この結果は、印加電圧によって表面での反応性を能動的に制御できる可能性を示唆しており、触媒設計などにおいて重要な知見となり得ます。

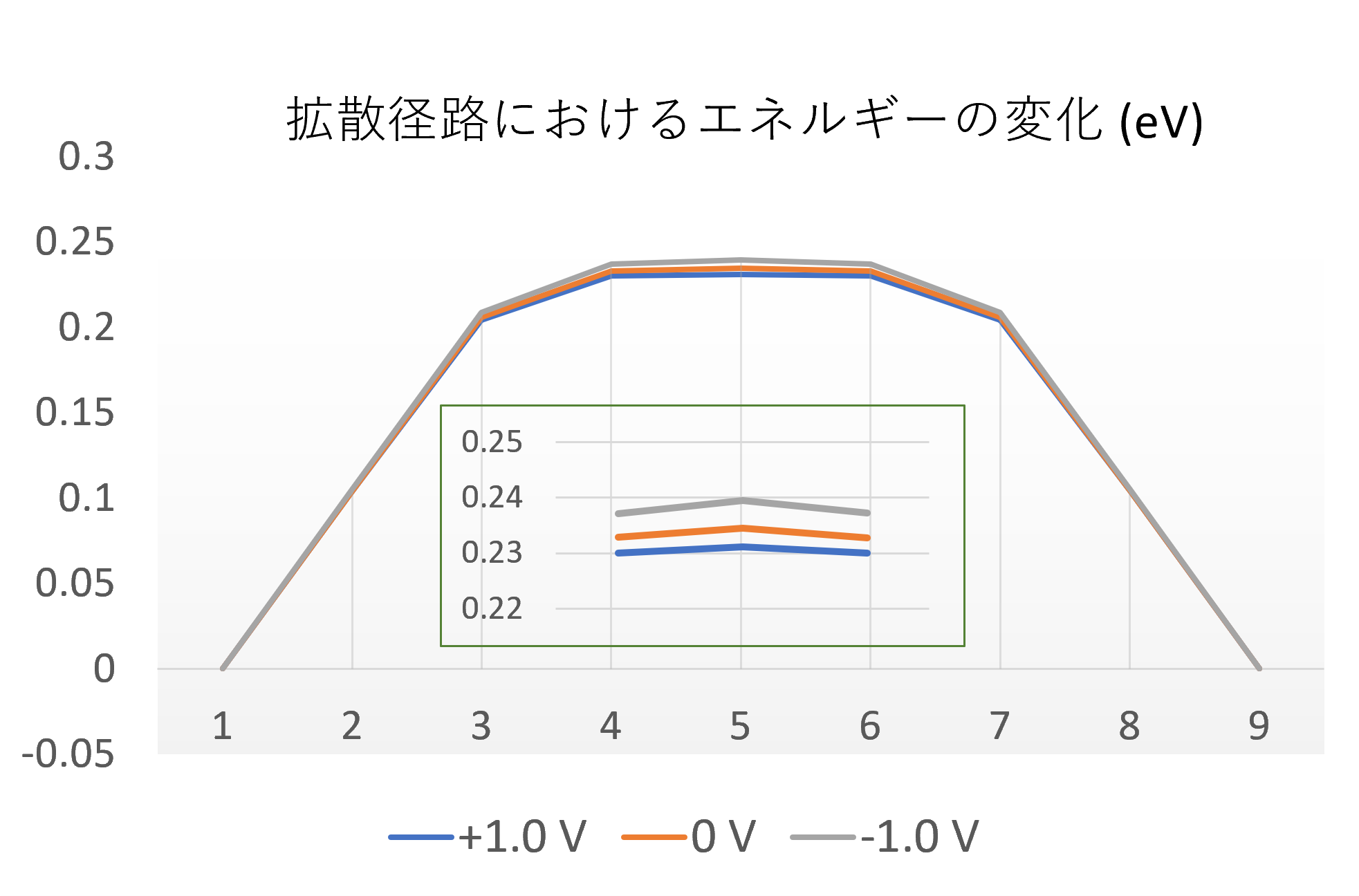
図5. 印加電圧による水素原子の拡散エネルギー障壁の変化。


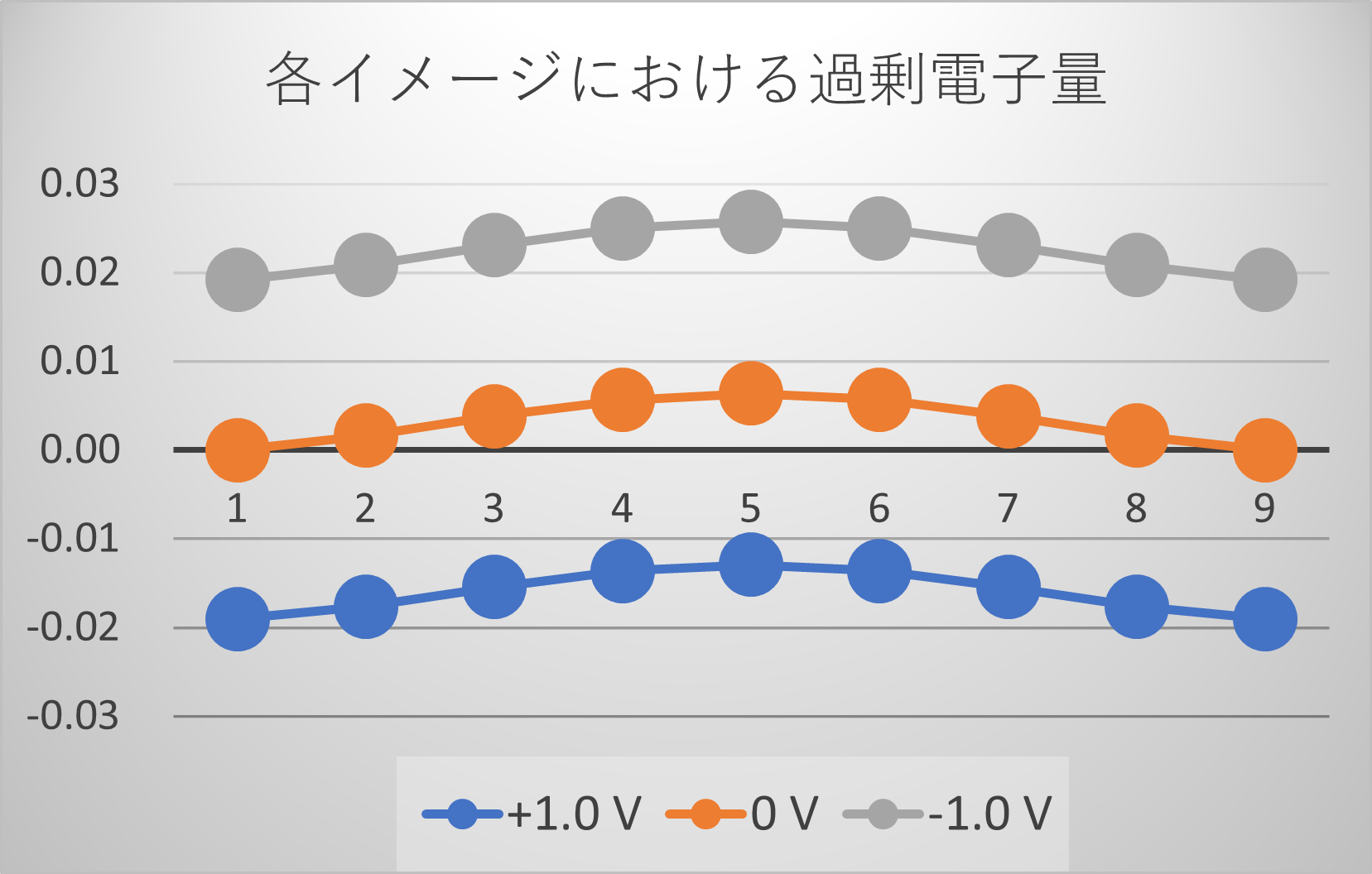
図6. 電圧印加時に各イメージにおける過剰電子量。

Constant-μ法を用いたNEB計算の最も重要な特徴は、拡散経路に沿って系の過剰電荷量が変化する点です (図6)。これは、反応の進行に伴い、電極（スラブ）と吸着分子の間で電子の授受が起こり、常に一定の電位を保つように電荷量が調整されることを物理的に正しく表現しています。従来の電子数一定の計算ではこのような電荷移動を考慮できず、反応中の電位が変動してしまいます 。実際に、Al(111)表面での水分子の拡散を解析した研究では、Constant-μ法を用いることで初めて、印加電圧によって活性化エネルギーだけでなく、水分子の配向を含む拡散メカニズム自体が大きく変化する様子が捉えられており、本手法の有効性が実証されています [3, 4]。

NEB計算が収束した際の出力の一部を以下に示します（出力例2）。原子に働く力（force (neb)）とFCPに働く力（force (fcp)）の両方が、設定された収束しきい値を下回っていることが確認できます。

convergence check...      36
force(neb):  6.927905388501061E-005  1.000000000000000E-004 T
force(fcp):  9.401847207018976E-006  5.000000000000000E-004 T
NEB converged ...
write down data replica...

出力例2. Constant-μ NEB計算の収束判定部分の出力例。

まとめ#

本解析では、第一原理計算ソフトウェアAdvance/PHASEに実装されているConstant-μ（FCP）法を用い、電極電位を一定に保った条件でのシミュレーション事例を紹介しました。その結果、吸着分子の安定構造（特に配向）が印加電圧に強く依存すること、そして分子の拡散経路や活性化エネルギーも電圧によって大きく変化し、その評価にConstant-μ NEB法が有効であることが明らかになりました。本手法は、反応中に電極と分子の間で起こる電荷移動を正しく記述できるため、電気化学反応やSTM実験のより現実的なシミュレーションを可能にします。Constant-μ法は、材料表面での電気化学的な現象を原子・電子レベルで解明するための強力なツールとなります。

参考文献#

  1. N. Bonnet, T. Morishita, O. Sugino, and M. Otani, "First-principles molecular dynamics at a constant electrode potential”, Phys. Rev. Lett. 109, 266101 (2012).
  2. M. Otani and O. Sugino, "First-principles calculations of charged surfaces and interfaces: A plane-wave nonrepeated slab approach", Phys. Rev. B 73, 115407 (2006).
  3. 胡春平、大谷実、"定電位電極表面における分子の吸着構造と拡散過程の第一原理シミュレーション"、2015年真空・表面科学合同講演会（つくば）、 3Fp11Y (2015).
  4. S. Hagiwara, C. Hu, S. Nishihara, and M. Otani, "Bias-dependent diffusion of a H₂O molecule on metal surfaces by the first-principles method under the grand-canonical ensemble", Phys. Rev. Materials 5, 065001 (2021).

関連ページ#